Hostname: page-component-669899f699-qzcqf Total loading time: 0 Render date: 2025-05-02T11:45:17.406Z Has data issue: false hasContentIssue false
  • English
  • Français

Well-posedness of quasilinear parabolic equations in time-weighted spaces

Part of: Parabolic equations and systems Equations of mathematical physics and other areas of application Partial differential equations

Published online by Cambridge University Press:  26 November 2024

Bogdan-Vasile Matioc Open the ORCID record for Bogdan-Vasile Matioc [Opens in a new window]  and
Christoph Walker Open the ORCID record for Christoph Walker [Opens in a new window]
Bogdan-Vasile Matioc
Affiliation:
Fakultät für Mathematik, Universität Regensburg, 93053 Regensburg, Germany ([email protected])
Christoph Walker
Affiliation:
Leibniz Universität Hannover, Institut für Angewandte Mathematik, Welfengarten 1, 30167 Hannover, Germany ([email protected]) (corresponding author)
Get access Rights & Permissions [Opens in a new window]

Abstract

Well-posedness in time-weighted spaces of certain quasilinear (and semilinear) parabolic evolution equations 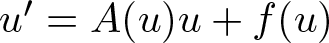$u'=A(u)u+f(u)$ is established. The focus lies on the case of strict inclusions 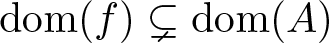$\mathrm{dom}(f)\subsetneq \mathrm{dom}(A)$ of the domains of the nonlinearities 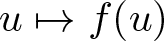$u\mapsto f(u)$ and 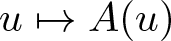$u\mapsto A(u)$. Based on regularizing effects of parabolic equations it is shown that a semiflow is generated in intermediate spaces. In applications this allows one to derive global existence from weaker a priori estimates. The result is illustrated by examples of chemotaxis systems.

Keywords

quasilinear parabolic problemsemiflowwell-posednesstime-weighted-spaceschemotaxis equations

MSC classification

Primary: 35B40: Asymptotic behavior of solutions
Secondary: 35K58: Semilinear parabolic equations 35K59: Quasilinear parabolic equations 35Q92: PDEs in connection with biology and other natural sciences
Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , First View , pp. 1 - 33
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press on behalf of The Royal Society of Edinburgh

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Acquistapace, P. and Terreni, B.. On quasilinear parabolic systems. Math. Ann. 282 (1988), 315–335.CrossRefGoogle Scholar
Amann, H.. GewöHnliche Differentialgleichungen, de Gruyter Lehrbuch. [de Gruyter Textbook] (Walter de Gruyter & Co, Berlin, 1983).Google Scholar
Amann, H.. Existence and regularity for semilinear parabolic evolution equations. Ann. Scuola Norm. Sup. Pisa Cl. Sci (4) 11 (1984), 593–676.Google Scholar
Amann, H.. Dynamic theory of quasilinear parabolic equations. I. Abstract evolution equations. Nonlinear Anal. 12 (1988), 895–919.CrossRefGoogle Scholar
Amann, H.. Highly degenerate quasilinear parabolic systems. Ann. Scuola Norm. Sup. Pisa Cl. Sci (4) 18 (1991), 135–166.Google Scholar
Amann, H.. Multiplication in Sobolev and Besov spaces. In: Nonlinear Analysis. A tribute in honour of Giovanni Prodi. Sc. Norm. Super. di Pisa Quaderni, Scuola Norm. Sup. Pisa. (1991), 27–50.Google Scholar
Amann, H.. Nonhomogeneous linear and quasilinear elliptic and parabolic boundary value problems. Function spaces, Differential Operators and Nonlinear Analysis (Friedrichroda, 1992), vol. 133 of Teubner-Texte Math., (Teubner, Stuttgart, 1993).Google Scholar
Amann, H.. Linear and Quasilinear Parabolic problems. Vol. I, vol. 89 of Monographs in Mathematics (Birkhäuser Boston, Inc., Boston, MA, 1995).CrossRefGoogle Scholar
Amann, H.. On the strong solvability of the Navier–Stokes equations. J. Math. Fluid Mech. 2 (2000), 16–98.CrossRefGoogle Scholar
Amann, H. and Walker, C.. Local and global strong solutions to continuous coagulation-fragmentation equations with diffusion. J. Differ. Equ. 218 (2005), 159–186.CrossRefGoogle Scholar
Angenent, S. B.. Nonlinear analytic semiflows. Proc. R. Soc. Edinburgh Sect. A 115 (1990), 91–107.CrossRefGoogle Scholar
Biler, P.. Local and global solvability of some parabolic systems modelling chemotaxis. Adv. Math. Sci. Appl. 8 (1998), 715–743.Google Scholar
Clément, P. and Li, S.. Abstract parabolic quasilinear equations and application to a groundwater flow problem. Adv. Math. Sci. Appl. 3 (1993/94), 17–32.Google Scholar
Clément, P. and Simonett, G.. Maximal regularity in continuous interpolation spaces and quasilinear parabolic equations. J. Evol. Equ. 1 (2001), 39–67.CrossRefGoogle Scholar
Da Prato, G.. Fully nonlinear equations by linearization and maximal regularity, and applications. Partial Differential Equations and Functional analysis, vol. 22 of Progr. Nonlinear Differential Equations Appl., (Birkhäuser Boston, Boston, MA, 1996).Google Scholar
Da Prato, G. and Grisvard, P.. Equations d’évolution abstraites non linéaires de type parabolique. Ann. Mat. Pura Appl. (4) 120 (1979), 329–396.CrossRefGoogle Scholar
Da Prato, G. and Lunardi, A.. Stability, instability and center manifold theorem for fully nonlinear autonomous parabolic equations in Banach space. Arch. Rational Mech. Anal. 101 (1988), 115–141.CrossRefGoogle Scholar
Guidetti, D.. Convergence to a stationary state and stability for solutions of quasilinear parabolic equations. Ann. Mat. Pura Appl. (4) 151 (1988), 331–358.CrossRefGoogle Scholar
Jiang, J., Laurençot, P. and Zhang, Y.. Global existence, uniform boundedness, and stabilization in a chemotaxis system with density-suppressed motility and nutrient consumption. Commun. Partial Differ. Equ. 47 (2022), 1024–1069.CrossRefGoogle Scholar
Köhne, M., Prüss, J. and Wilke, M.. On quasilinear parabolic evolution equations in weighted Lp-spaces. J. Evol. Equ. 10 (2010), 443–463.CrossRefGoogle Scholar
Laurençot, P.. Global bounded and unbounded solutions to a chemotaxis system with indirect signal production. Discrete Contin. Dyn. Syst. Ser. B 24 (2019), 6419–6444.Google Scholar
Laurençot, P. and Walker, C.. Well-posedness of the coagulation-fragmentation equation with size diffusion. Differ. Integral Equ. 35 (2022), 211–240.Google Scholar
LeCrone, J., Prüss, J. and Wilke, M.. On quasilinear parabolic evolution equations in weighted Lp-spaces II. J. Evol. Equ. 14 (2014), 509–533.CrossRefGoogle Scholar
LeCrone, J. and Simonett, G.. On quasilinear parabolic equations and continuous maximal regularity. Evol. Equ. Control Theory. 9 (2020), 61–86.CrossRefGoogle Scholar
Lunardi, A.. Abstract quasilinear parabolic equations. Math. Ann. 267 (1984), 395–415.CrossRefGoogle Scholar
Lunardi, A.. Asymptotic exponential stability in quasilinear parabolic equations. Nonlinear Anal. 9 (1985), 563–586.CrossRefGoogle Scholar
Lunardi, A.. Global solutions of abstract quasilinear parabolic equations. J. Differ. Equ.. 58 (1985), 228–242.CrossRefGoogle Scholar
Lunardi, A.. On the local dynamical system associated to a fully nonlinear abstract parabolic equation. Nonlinear Analysis and Applications (Arlington, Tex. 1986), vol. 109 of Lecture Notes in Pure and Appl. Math., (Dekker, New York, 1987).Google Scholar
Lunardi, A.. Analytic Semigroups and Optimal Regularity in Parabolic Problems, Progress in Nonlinear Differential Equations and Their Applications. Vol.16 (Birkhäuser Verlag, Basel, 1995).Google Scholar
Matioc, B.-V. and Walker, C.. On the principle of linearized stability in interpolation spaces for quasilinear evolution equations. Monatsh. Math. 191 (2020), 615–634.CrossRefGoogle Scholar
Prüss, J.. Maximal regularity for evolution equations in Lp -spaces, Conf. Semin. Mat. Univ. Bari (2002), 2003), .Google Scholar
Prüss, J. and Simonett, G.. Moving Interfaces and Quasilinear Parabolic Evolution equations, vol. 105 of Monographs in Mathematics (Birkhäuser/Springer, Cham, 2016).Google Scholar
Prüss, J., Simonett, G. and Wilke, M.. Critical spaces for quasilinear parabolic evolution equations and applications. J. Differ. Equ. 264 (2018), 2028–2074.CrossRefGoogle Scholar
Prüss, J. and Wilke, M.. Addendum to the paper “On quasilinear parabolic evolution equations in weighted Lp-spaces II” [MR3250797]. J. Evol. Equ. 17 (2017), 1381–1388.CrossRefGoogle Scholar
Triebel, H.. Interpolation Theory, Function Spaces, Differential Operators (North-Holland, Amsterdam, 1978).Google Scholar
Walker, C.. Global existence for an age and spatially structured haptotaxis model with nonlinear age-boundary conditions. Eur. J. Appl. Math. 19 (2008), 113–147.CrossRefGoogle Scholar
Walker, C. and Webb, G. F.. Global existence of classical solutions for a haptotaxis model. SIAM J. Math. Anal. 38 (2006/07), 1694–1713.CrossRefGoogle Scholar