Hostname: page-component-669899f699-vbsjw Total loading time: 0 Render date: 2025-05-02T15:29:33.325Z Has data issue: false hasContentIssue false
  • English
  • Français

The space of commuting elements in a Lie group and maps between classifying spaces

Part of: Homology and homotopy of topological groups and related structures Fiber spaces and bundles

Published online by Cambridge University Press:  27 October 2023

Daisuke Kishimoto ,
Masahiro Takeda  and
Mitsunobu Tsutaya
Daisuke Kishimoto
Affiliation:
Faculty of Mathematics, Kyushu University, Fukuoka 819-0395, Japan ([email protected])
Masahiro Takeda
Affiliation:
Institute for Liberal Arts and Sciences, Kyoto University, Kyoto 606-8316, Japan ([email protected])
Mitsunobu Tsutaya
Affiliation:
Faculty of Mathematics, Kyushu University, Fukuoka 819-0395, Japan ([email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

Let $\pi$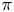 be a discrete group, and let $G$ 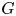be a compact-connected Lie group. Then, there is a map $\Theta \colon \mathrm {Hom}(\pi,G)_0\to \mathrm {map}_*(B\pi,BG)_0$ 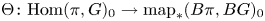between the null components of the spaces of homomorphisms and based maps, which sends a homomorphism to the induced map between classifying spaces. Atiyah and Bott studied this map for $\pi$ 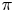a surface group, and showed that it is surjective in rational cohomology. In this paper, we prove that the map $\Theta$ 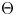is surjective in rational cohomology for $\pi =\mathbb {Z}^m$ 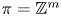and the classical group $G$ 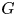except for $SO(2n)$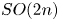, and that it is not surjective for $\pi =\mathbb {Z}^m$ 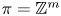with $m\ge 3$ 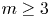and $G=SO(2n)$ 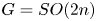with $n\ge 4$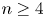. As an application, we consider the surjectivity of the map $\Theta$ 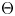in rational cohomology for $\pi$ 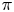a finitely generated nilpotent group. We also consider the dimension of the cokernel of the map $\Theta$ 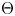in rational homotopy groups for $\pi =\mathbb {Z}^m$ 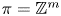and the classical groups $G$ 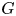except for $SO(2n)$.

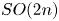Keywords

space of commuting elementsLie groupclassifying spaceflat connectionrational cohomology

MSC classification

Primary: 55R37: Maps between classifying spaces
Secondary: 57T10: Homology and cohomology of Lie groups
Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , First View , pp. 1 - 21
Check for updates
Copyright
Copyright © The Author(s), 2023. Published by Cambridge University Press on behalf of The Royal Society of Edinburgh

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Adem, A. and Cohen, F. R.. Commuting elements and spaces of homomorphisms. Math. Ann. 338 (2007), 587–626.CrossRefGoogle Scholar
Adem, A., Cohen, F. R. and Torres-Giese, E.. Commuting elements, simplicial spaces, and filtrations of classifying spaces. Math. Proc. Cambridge Philos. Soc. 152 (2012), 91–114.CrossRefGoogle Scholar
Adem, A., Gómez, J. M. and Gritschacher, S.. On the second homotopy group of spaces of commuting elements in Lie groups. IMRN 2022 (2022), 19617–19689.CrossRefGoogle Scholar
Atiyah, M. F. and Bott, R.. The Yang–Mills equations over Riemann surfaces. Philos. Trans. R. Soc. London, Ser. A 308 (1983), 523–615.Google Scholar
Baird, T. J.. Cohomology of the space of commuting $n$-tuples in a compact Lie group. Algebra Geom. Topol. 7 (2007), 737–754.CrossRefGoogle Scholar
Baird, T., Jeffrey, L. C. and Selick, P.. The space of commuting $n$-tuples in $SU(2)$. Ill. J. Math. 55 (2011), 805–813.Google Scholar
Baird, T. and Ramras, D. A.. Smoothing maps into algebraic sets and spaces of flat connections. Geom. Dedicata 174 (2015), 359–374.CrossRefGoogle Scholar
Bergeron, M.. The topology of nilpotent representations in reductive groups and their maximal compact subgroups. Geom. Topol. 19 (2015), 1383–1407.CrossRefGoogle Scholar
Bergeron, M. and Silberman, L.. A note on nilpotent representations. J. Group Theory 19 (2016), 125–135.CrossRefGoogle Scholar
Bott, R.. The space of loops on a Lie group. Mich. Math. J. 5 (1958), 35–61.CrossRefGoogle Scholar
Broto, C., Levi, R. and Oliver, B.. The theory of $p$-local groups: a survey, homotopy theory: relations with algebraic geometry, group cohomology, and algebraic $K$-theory. Contemporary Mathematics, vol. 346, pp. 51–84 (Providence, RI: American Mathematical Society, 2004).Google Scholar
Crabb, M. C.. Spaces of commuting elements in $SU(2)$. Proc. Edinburgh Math. Soc. 54 (2011), 67–75.CrossRefGoogle Scholar
Félix, Y., Halperin, S. and Thomas, J.-C.. Rational homotopy theory. Graduate Texts in Mathematics, vol. 205 (New York: Springer-Verlag, 2001).CrossRefGoogle Scholar
Fuchs, M.. Verallgemeinerte homotopie-homomorphismen und klassifizierende Raüme. Math. Ann. 161 (1965), 197–230.CrossRefGoogle Scholar
Goldman, W. M.. Topological components of spaces of representations. Invent. Math. 93 (1988), 557–607.CrossRefGoogle Scholar
Gómez, J. M., Pettet, A. and Souto, J.. On the fundamental group of $\mathrm {Hom}(\mathbb {Z}^k,G)$. Math. Z. 271 (2012), 33–44.CrossRefGoogle Scholar
Grodal, J.. The classification of $p$-compact groups and homotopical group theory. Proceedings of the International Congress of Mathematicians, vol. II, pp. 973–1001 (New Delhi: Hindustan Book Agency, 2010).Google Scholar
Hasegawa, K.. Minimal models of nilmanifolds. Proc. Am. Math. Soc. 106 (1989), 65–71.CrossRefGoogle Scholar
Hilton, P., Mislin, G. and Roitberg, J.. Localization of nilpotent groups and spaces. In North-Holland Mathematics Studies, vol. 15, Notas de Matemática (Notes on Mathematics), vol. 55 (Amsterdam, Oxford/New York: North-Holland Publishing Co./American Elsevier Publishing Co., Inc., 1975).Google Scholar
Jackowski, S., McClure, J. and Oliver, B.. Maps between classifying spaces revisited. The Čech centennial (Boston, MA, 1993), 263–298. Contemporary Mathematics, vol. 181 (Providence, RI: American Mathematical Society, 1995).CrossRefGoogle Scholar
Kishimoto, D. and Takeda, M.. Spaces of commuting elements in the classical groups. Adv. Math. 386 (2021), 107809.CrossRefGoogle Scholar
Kishimoto, D. and Takeda, M.. Torsion in the space of commuting elements in a Lie group. Can. J. Math. (accepted).Google Scholar
Kishimoto, D. and Kono, A.. On the cohomology of free and twisted loop spaces. J. Pure Appl. Algebra 214 (2010), 646–653.CrossRefGoogle Scholar
Milnor, J.. Construction of universal bundles, II. Ann. Math. 63 (1956), 430–436.CrossRefGoogle Scholar
Ramras, D. A. and Stafa, M.. Hilbert–Poincaré series for spaces of commuting elements in Lie groups. Math. Z. 292 (2019), 591–610.CrossRefGoogle Scholar
Ramras, D. A. and Stafa, M.. Homological stability for spaces of commuting elements in Lie groups. Int. Math. Res. Not. 2021 (2021), 3927–4002.Google Scholar
Stasheff, J. D.. Homotopy associativity of H-spaces, I & II. Trans. Am. Math. Soc. 108 (1963), 275–292. 293–312.Google Scholar
Sullivan, D.. Geometric topology, part I: localization, periodicity and Galois symmetry. K-Monographs in Math (Dordrecht: Kluwer Academic Publishers, 2004).Google Scholar
Tsutaya, M.. Mapping spaces from projective spaces. Homol. Homotopy Appl. 18 (2016), 173–203.CrossRefGoogle Scholar