Hostname: page-component-669899f699-8p65j Total loading time: 0 Render date: 2025-04-30T11:37:15.263Z Has data issue: false hasContentIssue false
  • English
  • Français

Regularity of the extremal solutions associated with elliptic systems

Part of: Elliptic equations and systems

Published online by Cambridge University Press:  27 December 2018

A. Aghajani  and
C. Cowan
A. Aghajani
Affiliation:
School of Mathematics, Iran University of Science and Technology, Narmak, Tehran, Iran and School of Mathematics, Institute for Research in Fundamental Sciences (IPM), P.O. Box 19395-5746, Tehran, Iran ([email protected].)
C. Cowan
Affiliation:
Department of Mathematics, University of Manitoba, Winnipeg, Manitoba, Canada ([email protected].)
Get access Rights & Permissions [Opens in a new window]

Abstract

We examine the elliptic system given by

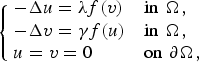$$\left\{ {\matrix{ {-\Delta u = \lambda f(v)} \hfill & {{\rm in }\,\,\Omega ,} \hfill \cr {-\Delta v = \gamma f(u)} \hfill & {{\rm in }\,\,\Omega ,} \hfill \cr {u = v = 0} \hfill & {{\rm on }\,\,\partial \Omega ,} \hfill \cr } } \right.$$
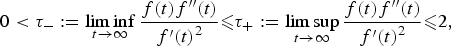where λ, γ are positive parameters, Ω is a smooth bounded domain in ℝN and f is a C2 positive, nondecreasing and convex function in [0, ∞) such that f(t)/t → ∞ as t → ∞. Assuming
$$0 < \tau _-: = \mathop {\lim \inf }\limits_{t\to \infty } \displaystyle{{f(t){f}^{\prime \prime}(t)} \over {{f}^{\prime}{(t)}^2}} \les \tau _ + : = \mathop {\lim \sup }\limits_{t\to \infty } \displaystyle{{f(t){f}^{\prime \prime}(t)} \over {{f}^{\prime}{(t)}^2}} \les 2,$$
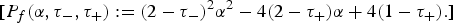 we show that the extremal solution (u*, v*) associated with the above system is smooth provided that N < (2α*(2 − τ+) + 2τ+)/(τ+)max{1, τ+}, where α* > 1 denotes the largest root of the second-order polynomial
$$[P_{f}(\alpha,\tau_{-},\tau_{+}):=(2-\tau_{-})^{2} \alpha^{2}- 4(2-\tau_{+})\alpha+4(1-\tau_{+}).]$$
 As a consequence, u*, v* ∈ L∞(Ω) for N < 5. Moreover, if τ− = τ+, then u*, v* ∈ L∞(Ω) for N < 10.

Keywords

extremal solutionstable solutionregularity of solutionselliptic systems

MSC classification

Primary: 35J47: Second-order elliptic systems
Secondary: 35J61: Semilinear elliptic equations
Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 149 , Issue 4 , August 2019 , pp. 1037 - 1046
Copyright
Copyright © Royal Society of Edinburgh 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

1Aghajani, A.. New a priori estimates for semistable solutions of semilinear elliptic equations. Potential Anal. 44 (2016), 729–744.Google Scholar
2Brezis, H. and Vazquez, L.. Blow-up solutions of some nonlinear elliptic problems. Rev. Mat. Univ. Complut. Madrid 10 (1997), 443–469.Google Scholar
3Cabré, X.. Regularity of minimizers of semilinear elliptic problems up to dimension 4. Comm. Pure Appl. Math. 63 (2010), 1362–1380.Google Scholar
4Cowan, C.. Regularity of the extremal solutions in a Gelfand systems problem. Adv. Nonlinear Stud. 11 (2011), 695–700.Google Scholar
5Cowan, C.. Regularity of stable solutions of a Lane-Emden type system. Methods Appl. Anal. 22(3) (2015), 301–311.Google Scholar
6Cowan, C. and Ghoussoub, N.. Regularity of semi-stable solutions to fourth order nonlinear eigenvalue problems on general domains, Calc. Var. Partial Differ. Equ., 49(1–2) (2014), 291–305.Google Scholar
7Dávila, J. and Goubet, O.. Partial regularity for a Liouville system. Dscrete Contin. Dyn. Syst. 34(6) (2014), 2495–2503.Google Scholar
8Dupaigne, L.. Stable solutions of elliptic partial differential equations. Chapman & Hall/CRC Monographs and Surveys in Pure and Applied Mathematics, 2011.Google Scholar
9Dupaigne, L., Farina, A. and Sirakov, B.. Regularity of the extremal solutions for the Liouville system, Geometric Partial Differential Equations proceedings CRM Series, vol. 15, Ed. Norm., Pisa, 2013, pp. 139–144.Google Scholar
10Hajlaoui, H.. On the regularity and partial regularity of extremal solutions of a Lane-Emden system, https://arxiv.org/pdf/1611.05488.pdf.Google Scholar
11Montenegro, M.. Minimal solutions for a class of elliptic systems. Bull. London Math. Soc. 37 (2005), 405–416.Google Scholar
12Nedev, G.. Regularity of the extremal solution of semilinear elliptic equations. C. R. Acad. Sci. Paris S‘er. I Math. 330 (2000), 997–1002.Google Scholar
13Serrin, J.. Local behavior of solutions of quasi-linear equations. Acta Math. 111 (1964), 247–302.Google Scholar
14Trudinger, N. S.. Linear elliptic operators with measurable coefficients. Ann. Scuola Norm. Sup. Pisa 27(3) (1973), 265–308.Google Scholar
15Villegas, S.. Boundedness of extremal solutions in dimension 4. Adv. Math. 235 (2013), 126–133.Google Scholar
16Ye, D. and Zhou, F.. Boundedness of the extremal solution for semilinear elliptic problems. Commun. Contemp. Math. 4 (2002), 547–558.Google Scholar