Hostname: page-component-669899f699-2mbcq Total loading time: 0 Render date: 2025-04-29T17:25:35.434Z Has data issue: false hasContentIssue false
  • English
  • Français

A note on right-nil and strong-nil skew braces

Part of: Hopf algebras, quantum groups and related topics Special aspects of infinite or finite groups Radicals and radical properties of rings

Published online by Cambridge University Press:  18 December 2024

A Ballester-Bolinches Open the ORCID record for A Ballester-Bolinches [Opens in a new window] ,
M Ferrara Open the ORCID record for M Ferrara [Opens in a new window] ,
V Pérez-Calabuig Open the ORCID record for V Pérez-Calabuig [Opens in a new window]  and
M Trombetti Open the ORCID record for M Trombetti [Opens in a new window]
A Ballester-Bolinches
Affiliation:
Departament de Matemàtiques, Universitat de València, Dr. Moliner, 50, 46100 Burjassot, València, Spain ([email protected])
M Ferrara
Affiliation:
Dipartimento di Matematica e Fisica, Università degli Studi della Campania “Luigi Vanvitelli”, viale Lincoln 5, Caserta, Italy ([email protected])
V Pérez-Calabuig
Affiliation:
Departament de Matemàtiques, Universitat de València, Dr. Moliner, 50, 46100 Burjassot, València, Spain ([email protected])
M Trombetti*
Affiliation:
Dipartimento di Matematica e Applicazioni “Renato Caccioppoli”, Università degli Studi di Napoli Federico II, Complesso Universitario Monte S. Angelo, Via Cintia, Napoli, Italy ([email protected]) (corresponding author)
*
*Corresponding author.
Get access Rights & Permissions [Opens in a new window]

Abstract

Nilpotency concepts for skew braces are among the main tools with which we are nowadays classifying certain special solutions of the Yang–Baxter equation, a consistency equation that plays a relevant role in quantum statistical mechanics and in many areas of mathematics. In this context, two relevant questions have been raised in F. Cedó, A. Smoktunowicz and L. Vendramin (Skew left braces of nilpotent type. Proc. Lond. Math. Soc. (3) 118 (2019), 1367–1392) (see questions 2.34 and 2.35) concerning right- and central nilpotency. The aim of this short note is to give a negative answer to both questions: thus, we show that a finite strong-nil brace B need not be right-nilpotent. On a positive note, we show that there is one (and only one, by our examples) special case of the previous questions that actually holds. In fact, we show that if B is a skew brace of nilpotent type and 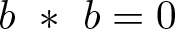$b\ \ast \ b=0$ for all 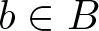$b\in B$, then B is centrally nilpotent.

Keywords

centrally nilpotent skew braceright nilpotent skew braceright-nil skew bracestrong-nilskew brace

MSC classification

Primary: 16T25: Yang-Baxter equations 20F18: Nilpotent groups 16N99: None of the above, but in this section
Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , First View , pp. 1 - 9
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press on behalf of The Royal Society of Edinburgh

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

The GAP Group: GAP – Groups, Algorithms, and Programming. 4 (2024) http://www.gap-system.org.Google Scholar
Ballester-Bolinches, A. and Esteban-Romero, R.. Triply factorised groups and the structure of skew left braces. Commun. Math. Stat. 10 (2022), 353–370.CrossRefGoogle Scholar
Ballester-Bolinches, A., Esteban-Romero, R., Ferrara, M., Perez-Calabuig, V. and Trombetti, M.. Central nilpotency of left skew braces and solutions of the Yang–Baxter equation. submitted; ArXiv:2310.07474.Google Scholar
Baxter, R. J.. Partition function of the eight-vertex lattice model. Ann. Physics 70 (1972), 193–228.CrossRefGoogle Scholar
Bonatto, M. and Jedlička, P.. Central nilpotency of skew braces. J. Algebra Appl (12) 22 (2022), . 10.1142/S0219498823502559Google Scholar
Cedó, F., Jespers, E., Kubat, L., Van Antwerpen, A. and Verwimp, C.. On various types of nilpotency of the structure monoid and group of a set-theoretic solution of the Yang–Baxter equation. J. Pure Appl. Algebra 227 (2023), .CrossRefGoogle Scholar
Cedó, F., Smoktunowicz, A. and Vendramin, L.. Skew left braces of nilpotent type. Proc. Lond. Math. Soc. (3) 118 (2019), 1367–1392.CrossRefGoogle Scholar
Drinfel’d, V.. Hopf algebras and the Yang–Baxter equation, Yang–Baxter Equation in Integrable Systems, (World Scientific, 1990).Google Scholar
Drinfel’d, V.. On some unsolved problems in quantum group theory, Quantum Groups, (Springer, Berlin, 1992).Google Scholar
Faddeev, L., Reshetikhin, N. and Takhtajan, L.. Quantum groups, Braid Group, Knot Theory and Statistical Mechanics, (World Scientific, Teaneck, NJ, 1989).Google Scholar
Gateva-Ivanova, T. and Cameron, P.. Multipermutation solutions of the Yang-Baxter equation. Comm. Math. Phys. 309 (2012), 583–621.CrossRefGoogle Scholar
Gateva-Ivanova, T.. Set-theoretic solutions of the Yang-Baxter equation, braces and symmetric groups. Adv. Math. 338 (2018), 649–701.CrossRefGoogle Scholar
Guarnieri, L. and Vendramin, L.. Skew-braces and the Yang-Baxter equation. Math. Comp. 86 (2017), 2519–2534.CrossRefGoogle Scholar
Jespers, E., Van Antwerpen, A. and Vendramin, L.. Nilpotency of skew braces and multipermutation solutions of the Yang-Baxter equation. Comm. Contemp. Math. 25, (2023), .CrossRefGoogle Scholar
Rump, W.. Braces, radical rings, and the quantum Yang-Baxter equation. J. Algebra 307 (2007), 153–170.CrossRefGoogle Scholar
Smoktunowicz, A.. A note on set-theoretic solutions of the Yang-Baxter equation. J. Algebra 500 (2018), 3–18.CrossRefGoogle Scholar
Vendramin, L. and Konovalov, O.. YangBaxter: combinatorial solutions for the Yang-Baxter equation, December 2022, version 0.10.2, https://gap-packages.github.io/YangBaxter/.Google Scholar
Yang, C. N.. Some exact results for the many-body problem in one dimension with repulsive delta-function interaction. Phys. Rev. Lett. 19, (1967), 1312–1315.CrossRefGoogle Scholar