Hostname: page-component-669899f699-ggqkh Total loading time: 0 Render date: 2025-04-29T23:52:55.168Z Has data issue: false hasContentIssue false
  • English
  • Français

Kolmogorov’s theorem for degenerate Hamiltonian systems with Hölder continuous parameters

Part of: Finite-dimensional Hamiltonian, Lagrangian, contact, and nonholonomic systems Hamiltonian and Lagrangian mechanics Nonlinear dynamics

Published online by Cambridge University Press:  26 November 2024

Jiayin Du ,
Yong Li  and
Hongkun Zhang
Jiayin Du
Affiliation:
College of Mathematics and Statistics, and Center for Mathematics and Interdisciplinary Sciences, Northeast Normal University, Changchun 130024, PR China ([email protected])
Yong Li
Affiliation:
College of Mathematics and Statistics, and Center for Mathematics and Interdisciplinary Sciences, Northeast Normal University, Changchun 130024, PR China College of Mathematics, Jilin University, Changchun 130012, PR China ([email protected]) (corresponding author)
Hongkun Zhang
Affiliation:
Department of Mathematics and Statistics, University of Massachusetts, Amherst 01003, United States Great Bay University, Dongguan, Guangdong 523000, PR China ([email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper, we investigate Kolmogorov-type theorems for small perturbations of degenerate Hamiltonian systems. These systems are index by a parameter ξ as 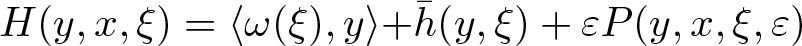$ H(y,x,\xi) = \langle\omega(\xi),y\rangle {+ \bar h(y,\xi)}+\varepsilon P(y,x,\xi,\varepsilon) $, where ɛ > 0. We assume that the frequency mapping 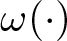$\omega(\cdot)$, 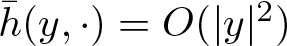$\bar h(y,\cdot)=O(|y|^2)$ and the perturbation 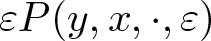$\varepsilon P(y,x,\cdot, \varepsilon)$ maintain Hölder continuity about ξ. We prove that the persistent invariant tori retain the same frequency as those of the unperturbed tori, under a certain topological degree condition and a weak convexity condition for the frequency mapping. Notably, this paper presents, to our understanding, pioneering results on the KAM theorem under such conditions with only assumption of Hölder continuous dependence of frequency mapping ω on the parameter.

Keywords

degeneracyfrequency-preservingHölder continuous parameterHamiltonian systeminvariant toriKolmogorov’s theorem

MSC classification

Primary: 37J40: Perturbations, normal forms, small divisors, KAM theory, Arnol'd diffusion
Secondary: 70H08: Nearly integrable Hamiltonian systems, KAM theory 70K43: Quasi-periodic motions and invariant tori
Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , First View , pp. 1 - 36
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press on behalf of The Royal Society of Edinburgh

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Arnold, V. I.. Proof of a theorem of A.N. Kolmogorov on the preservation of conditionally periodic motions under a small perturbation of the Hamiltonian. Uspehi Mat. Nauk. 18 (1963), 13–40. MR0163025.Google Scholar
Benettin, G., Galgant, L., Giorgilli, A. and Strelcyn, J.. A proof of Kolmogorov’s theorem on invariant tori using canonical transformations defined by the Lie method. Nuovo Cimento B 79 (1984), 201–223. MR0743977.CrossRefGoogle Scholar
Biasco, L., Chierchia, L. and Treschev, D.. Stability of nearly integrable, degenerate Hamiltonian systems with two degrees of freedom. J. Nonlinear Sci. 16 (2006), 79–107. MR2202903.CrossRefGoogle Scholar
Bounemoura, A.. Positive measure of KAM tori for finitely differentiable Hamiltonians. J. Éc. Polytech. Math. 7 (2020), 1113–1132. MR4167789.CrossRefGoogle Scholar
Bricmont, J., Gawedzki, K. and Kupiainen, A.. KAM theorem and quantum field theory. Commun. Math. Phys. 201 (1999), 699–727. MR1685894.CrossRefGoogle Scholar
Brjuno, A. D.. Nondegeneracy conditions in the Kolmogorov theorem. Sov. Math. Dokl. 45 (1992), 221–225. MR1171798.Google Scholar
Cheng, C. Q. and Sun, Y. S.. Existence of KAM tori in degenerate Hamiltonian systems. J. Differ. Equ. 114 (1994), 288–335. MR1302146.CrossRefGoogle Scholar
Chierchia, L.. Periodic solutions of the planetary N-body problem, XVIIth International Congress on Mathematical Physics, Hackensack, NJ: world scientific publishing, (2014), . MR3204477.Google Scholar
Chierchia, L. and Falcolini, C.. A direct proof of a theorem by Kolmogorov in Hamiltonian systems. Ann. Scuola Norm. Sup. Pisa Cl. Sci. 21 (1994), 541–593. MR1318772.Google Scholar
Chow, S. N., Li, Y. and Yi, Y. F.. Persistence of invariant tori on submanifolds in Hamiltonian systems. J. Nonlinear Sci. 12 (2002), 585–617. MR1938331.CrossRefGoogle Scholar
Cong, F. Z., Küpper, T., Li, Y. and You, J. G.. KAM-type theorem on resonant surfaces for nearly integrable Hamiltonian systems. J. Nonlinear Sci. 10 (2000), 49–68. MR1730569.CrossRefGoogle Scholar
de la Llave, R., González, A., Jorba, A. and Villanueva, J.. KAM theory without action-angle variables. Nonlinearity 18 (2005), 855–895. MR2122688.CrossRefGoogle Scholar
Eliasson, L. H.. Absolutely convergent series expansions for quasi-periodic motions. Math. Phys. Elect. J. 2 (1996), 1–33. MR1399458.Google Scholar
Féjoz, J.. Démonstration du ‘théorème d’Arnold’ sur la stabilité du système planétaire (d’après Herman). Ergod. Theory Dyn. Syst. 24 (2004), 1521–1582. MR2104595.CrossRefGoogle Scholar
Gallavotti, G.. Twistless KAM tori. Commun. Math. Phys. 164 (1994), 145–156. MR1288156.CrossRefGoogle Scholar
Gallavotti, G., Gentile, G. and Mastropietro, V.. Field theory and KAM tori. Math. Phys. Elect. J. 1 (1995), 1–13. MR1359460.Google Scholar
Han, Y. C., Li, Y. and Yi, Y. F.. Invariant tori in Hamiltonian systems with high order proper degeneracy. Ann. Henri Poincaré 10 (2010), 1419–1436. MR2639543.CrossRefGoogle Scholar
Heinz, H.. Non-degeneracy conditions in KAM theory. Indag. Math. (N.S.) 22 (2011), 241–256. MR2853608.Google Scholar
Herman, M. R.. Sur les courbes invariantes par les difféomorphismes de l’anneau. Vol. 1. (French) [On the curves invariant under diffeomorphisms of the annulus. Vol. 1] With an appendix by Albert Fathi. With an English summary. Astérisque (1983), . (Société Mathématique de France, Paris), 103–104. MR0728564.Google Scholar
Kolmogorov, A. N.. On conservation of conditionally periodic motions for a small change in Hamilton’s function. Dokl. Akad. Nauk SSSR 98 (1954), 527–530. MR0068687.Google Scholar
Koudjinan, C. E.. A KAM theorem for finitely differentiable Hamiltonian systems. J. Differ. Equ. 269 (2020), 4720–4750. MR4104457.CrossRefGoogle Scholar
Li, Y. and Yi, Y. F.. Persistence of invariant tori in generalized Hamiltonian systems. Ergod. Theory Dyn. Syst. 22 (2002), 1233–1261. MR1926285.CrossRefGoogle Scholar
Li, Y. and Yi, Y. F.. A quasi-periodic Poincaré’s theorem. Math. Ann. 326 (2003), 649–690. MR2003447.CrossRefGoogle Scholar
Meyer, K. R.. Periodic Solutions of the N-Body Problem. (Springer-Verlag, Berlin, 1999) MR1736548.CrossRefGoogle Scholar
Moser, J.. On invariant curves of area-preserving mapping of an annulus. Nachr. Akad. Wiss. Göttingen II (1962), 1–20. MR0147741.Google Scholar
Moser, J.. Convergent series expansions for quasi-periodic motions. Math. Ann. 169 (1967), 136–176. MR0208078.CrossRefGoogle Scholar
Motreanu, D., Motreanu, V. V. and Papageorgiou, N.. Topological and Variational Methods With Applications to Nonlinear Boundary Value Problems. (Springer Science+Business Media, LLC, 2014). MR3136201.CrossRefGoogle Scholar
Pöschel, J.. On elliptic lower-dimensional tori in Hamiltonian systems. Math. Z. 202 (1989), 559–608. MR1022821.CrossRefGoogle Scholar
Pöschel, J.. A KAM theorem for some nonlinear partial differential equations. Ann. Sc. Norm. Super. Pisa Cl. Sci. 23 (1996), 119–148. MR1401420.Google Scholar
Pöschel, J.. A lecture on the classical KAM theorem, Proc. Symp. Pure Math., Vol. 69, Providence, RI: American Mathematical Society, (2001). MR1858551CrossRefGoogle Scholar
Qian, W. C., Li, Y. and Yang, X.. Multiscale KAM theorem for Hamiltonian systems. J. Differ. Equ. 266 (2019), 70–86. MR3870557.CrossRefGoogle Scholar
Qian, W. C., Li, Y. and Yang, X.. Melnikov’s conditions in matrices. J. Dyn. Differ. Equ. 32 (2020), 1779–1795. MR4171876.CrossRefGoogle Scholar
Rüssmann, H. and Kleine Nenner, I.. Über invariante Kurven differenzierbarer Abbildungen eines Kreisringes. Nachr. Akad. Wiss. GöTtingen Math.-Phys. Kl. II (1970), 67–105. MR0273156.Google Scholar
Rüssmann, H.. Invariant tori in non-degenerate nearly integrable Hamiltonian systems. Regul. Chaotic Dyn. 6 (2001), 119–204. MR1843664.CrossRefGoogle Scholar
Salamon, D. A.. The Kolmogorov-Arnold-Moser theorem. Math. Phys. Electron. J. 10 (2004), 1–37. MR2111297.Google Scholar
Sevryuk, M. B.. KAM-stable Hamiltonians. J. Dyn. Control Syst. 1 (1995), 351–366. MR1354540.CrossRefGoogle Scholar
Sevryuk, M. B.. Partial perservation of frequencies in KAM theory. Nonlinearity 19 (2006), 1099–1140. MR2221801.CrossRefGoogle Scholar
Wayne, C. E.. An introduction to KAM theory. Lect. Appl. Math. 31 (1996), 3–29. MR1363023.Google Scholar
Xu, J. X. and Lu, X. Z.. General KAM theorems and their applications to invariant tori with prescribed frequencies. Regul. Chaotic Dyn. 21 (2016), 107–125. MR3457078.CrossRefGoogle Scholar
Xu, J. X., You, J. G. and Qiu, Q. J.. Invariant tori for nearly integrable Hamiltonian systems with degeneracy. Math. Z. 226 (1997), 375–387. MR1483538.CrossRefGoogle Scholar
Xu, J. X. and You, J. G.. Persistence of the non-twist torus in nearly integrable Hamiltonian systems. Proc. Amer. Math. Soc. 138 (2010), 2385–2395. MR2607868.CrossRefGoogle Scholar