Hostname: page-component-669899f699-tpknm Total loading time: 0 Render date: 2025-05-04T17:46:29.830Z Has data issue: false hasContentIssue false
  • English
  • Français

Finely quasiconformal mappings

Part of: Other generalizations Geometric function theory Linear function spaces and their duals

Published online by Cambridge University Press:  23 December 2024

Panu Lahti
Panu Lahti*
Affiliation:
Academy of Mathematics and Systems Science, Chinese Academy of Sciences, Beijing 100190, PR China ([email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

We introduce a relaxed version of the metric definition of quasiconformality that is natural also for mappings of low regularity, including 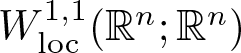$W_{\mathrm{loc}}^{1,1}({\mathbb R}^n;{\mathbb R}^n)$-mappings. Then we show on the plane that this relaxed definition can be used to prove Sobolev regularity, and that these ‘finely quasiconformal’ mappings are in fact quasiconformal.

Keywords

finely open setquasiconformal mappingSobolev mappingcapacityfine differentiability

MSC classification

Primary: 30C65: Quasiconformal mappings in $^n$, other generalizations
Secondary: 46E35: Sobolev spaces and other spaces of “smooth” functions, embedding theorems, trace theorems 31C40: Fine potential theory
Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , First View , pp. 1 - 25
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press on behalf of The Royal Society of Edinburgh

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Ambrosio, L., Fusco, N. and Pallara, D.. Functions of bounded variation and free discontinuity problems, Oxford Mathematical Monographs, (The Clarendon Press, Oxford University Press, New York, 2000).CrossRefGoogle Scholar
Balogh, Z. and Koskela, P.. Quasiconformality, quasisymmetry, and removability in Loewner spaces. Duke Math. J. 101 (2000), 554–577 With an appendix by Jussi Väisälä.CrossRefGoogle Scholar
Balogh, Z., Koskela, P. and Rogovin, S.. Absolute continuity of quasiconformal mappings on curves. Geom. Funct. Anal. 17 (2007), 645–664.CrossRefGoogle Scholar
Björn, A. and Björn, J.. Nonlinear potential theory on metric spaces. European Mathematical Society (EMS), ZüRich 17 (2011), EMS Tracts in Mathematics.Google Scholar
Carriero, M., Dal Maso, G., Leaci, A. and Pascali, E.. Relaxation of the nonparametric plateau problem with an obstacle. J. Math. Pures Appl. 9 (1988), 359–396.Google Scholar
Evans, L. C. and Gariepy, R. F.. Measure theory and fine properties of functions, Textbooks in Mathematics, Revised edition, (CRC Press, Boca Raton, FL, 2015).Google Scholar
Fang, A.. The ACL property of homeomorphisms under weak conditions. Acta Math. Sinica (N.S.) 14 (1998), 473–480.Google Scholar
Gehring, F. W.. Rings and quasiconformal mappings in space. Trans. Amer. Math. Soc. 103 (1962), 353–393.CrossRefGoogle Scholar
Gehring, F. W.. The Lp-integrability of the partial derivatives of a quasiconformal mapping. Acta Math. 130 (1973), 265–277.CrossRefGoogle Scholar
Heinonen, J., Koskela, P., Shanmugalingam, N. and Tyson, J.. Sobolev classes of Banach space-valued functions and quasiconformal mappings. J. Anal. Math. 85 (2001), 87–139.CrossRefGoogle Scholar
Heinonen, J., Koskela, P., Shanmugalingam, N. and Tyson, J.. Sobolev spaces on metric measure spaces. An approach based on upper gradients, New Mathematical Monographs, Vol. 27, (Cambridge University Press, Cambridge, 2015).Google Scholar
Kallunki, S. and Koskela, P.. Exceptional sets for the definition of quasiconformality. Amer. J. Math. 122 (2000), 735–743.CrossRefGoogle Scholar
Kallunki, S. and Martio, O.. ACL homeomorphisms and linear dilatation. Proc. Amer. Math. Soc. 130 (2002), 1073–1078.CrossRefGoogle Scholar
Kinnunen, J., Lehrbäck, J. and Vähäkangas, A.. Maximal function methods for Sobolev spaces, Mathematical Surveys and Monographs, Vol. 257, (American Mathematical Society, Providence, RI, 2021).Google Scholar
Koskela, P. and Rogovin, S.. Linear dilatation and absolute continuity. Ann. Acad. Sci. Fenn. Math. 30 (2005), 385–392.Google Scholar
Lahti, P.. A Federer-style characterization of sets of finite perimeter on metric spaces. Calc. Var. Partial Differential Equations 56 (2017), .CrossRefGoogle Scholar
Lahti, P.. A notion of fine continuity for BV functions on metric spaces. Potential Anal. 46 (2017), 279–294.CrossRefGoogle Scholar
Malý, J.. Absolutely continuous functions of several variables. J. Math. Anal. Appl. 231 (1999), 492–508.CrossRefGoogle Scholar
Malý, J. and Martio, O.. Lusin’s condition (N) and mappings of the class $W^{1,n}$. J. Reine Angew. Math. 458 (1995), 19–36.Google Scholar
Margulis, G. A. and Mostow, G. D.. The differential of a quasi-conformal mapping of a Carnot-Carathéodory space. Geom. Funct. Anal. 5 (1995), 402–433.CrossRefGoogle Scholar
Väisälä, J.. Lectures on n-dimensional quasiconformal mappings, Lecture Notes in Mathematics, Vol. 229, (Springer-Verlag, Berlin-New York, 1971).Google Scholar
Williams, M.. Dilatation, pointwise Lipschitz constants, and condition N on curves. Michigan Math. J. 63 (2014), 687–700.CrossRefGoogle Scholar