Hostname: page-component-669899f699-cf6xr Total loading time: 0 Render date: 2025-05-02T00:34:32.449Z Has data issue: false hasContentIssue false
  • English
  • Français

A pointwise characterisation of the PDE system of vectorial calculus of variations in L∞

Part of: Elliptic equations and systems Representations of solutions

Published online by Cambridge University Press:  01 February 2019

Birzhan Ayanbayev  and
Nikos Katzourakis
Birzhan Ayanbayev
Affiliation:
Department of Mathematics and Statistics, University of Reading, Whiteknights, PO Box 220, ReadingRG6 6AXBerkshire, UK ([email protected]; [email protected])
Nikos Katzourakis
Affiliation:
Department of Mathematics and Statistics, University of Reading, Whiteknights, PO Box 220, ReadingRG6 6AXBerkshire, UK ([email protected]; [email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

Let n, 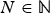$N \in {\open N}$ with 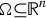$\Omega \subseteq {\open R}^n$ open. Given 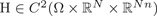${\rm H} \in C^2(\Omega \times {\open R}^N \times {\open R}^{Nn})$, we consider the functional 1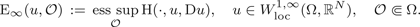

$${\rm E}_\infty (u,{\rm {\cal O}})\, : = \, \mathop {{\rm ess}\,\sup}\limits_{\rm {\cal O}} {\rm H}(\cdot, u,{\rm D}u),\quad u\in W_{{\rm loc}}^{1,\infty} (\Omega, {\open R}^N),\quad {\rm {\cal O}}{\Subset}\Omega.$$
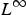The associated PDE system which plays the role of Euler–Lagrange equations in $L^\infty $ is 2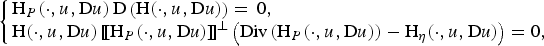
$$\left\{\matrix{{\rm H}_{P}(\cdot, u, {\rm D}u)\, {\rm D}\left({\rm H}(\cdot, u, {\rm D} u)\right) = \, 0, \hfill \cr {\rm H}(\cdot, u, {\rm D} u) \, [\![{\rm H}_{P}(\cdot, u, {\rm D} u)]\!]^\bot \left({\rm Div}\left({\rm H}_{P}(\cdot, u, {\rm D} u)\right)- {\rm H}_{\eta}(\cdot, u, {\rm D} u)\right) = 0,\hfill}\right.$$
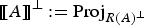 where $[\![A]\!]^\bot := {\rm Proj}_{R(A)^\bot }$. Herein we establish that generalised solutions to (2) can be characterised as local minimisers of (1) for appropriate classes of affine variations of the energy. Generalised solutions to (2) are understood as 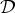${\cal D}$-solutions, a general framework recently introduced by one of the authors.

Keywords

∞-Laplaciangeneralised solutionscalculus of variations in L∞young measuresfully non-linear systems35J47

MSC classification

Primary: 35D99: None of the above, but in this section
Secondary: 35D40: Viscosity solutions 35J47: Second-order elliptic systems 35J92: Quasilinear elliptic equations with $p$-Laplacian 35J70: Degenerate elliptic equations 35J99: None of the above, but in this section
Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 150 , Issue 4 , August 2020 , pp. 1653 - 1669
Check for updates
Copyright
Copyright © Royal Society of Edinburgh 2019

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

1Abugirda, H. and Katzourakis, N.. 1D vectorial absolute minimisers in L ∞ under minimal assumptions. Proc. AMS 145 (2017), 2567–2575 (doi: https://doi.org/10.1090/proc/13421.CrossRefGoogle Scholar
2Aronsson, G.. Extension of functions satisfying Lipschitz conditions. Arkiv Mat. 6 (1967), 551–561.CrossRefGoogle Scholar
3Aronsson, G.. On the partial differential equation $u_x^2 u_{xx} + 2u_x u_y u_{xy} + u_y^2 u_{yy} = 0$. Arkiv Mat. 7 (1968), 395–425.CrossRefGoogle Scholar
4Barron, E. N., Jensen, R. and Wang, C.. The Euler equation and absolute minimizers of L ∞ functionals. Arch. Ration. Mech. Anal. 157 (2001a), 255–283.CrossRefGoogle Scholar
5Barron, E. N., Jensen, R. and Wang, C.. Lower semicontinuity of L ∞ functionals. Ann. I. H. Poincaré AN 18 (2001b), 495–517.CrossRefGoogle Scholar
6Castaing, C., de Fitte, P. R. and Valadier, M.. Young measures on topological spaces with applications in control theory and probability theory. Mathematics and its applications (Kluwer Academic Publishers, 2004).Google Scholar
7Crandall, M. G.. A visit with the ∞-Laplacian. In Calculus of variations and non-linear partial differential equations. Springer Lecture notes in Mathematics 1927 (Cetraro, Italy: CIME, 2005).Google Scholar
8Crandall, M. G., Ishii, H. and Lions, P.-L.. User's guide to viscosity solutions of 2nd order partial differential equations. Bull. AMS 27 (1992), 1–67.CrossRefGoogle Scholar
9Croce, G., Katzourakis, N. and Pisante, G.. ${\cal D}$-solutions to the system of vectorial calculus of variations in L ∞ via the singular value problem. Discrete Contin. Dyn. Syst. 37 (2017).CrossRefGoogle Scholar
10Danskin, J. M.. The theory of min-max with application. SIAM J. Appl. Math. 14 (1966), 641–664.CrossRefGoogle Scholar
11Edwards, R. E.. Functional analysis: theory and applications. Dover Books on Mathematics (2003).Google Scholar
12Evans, L. C.. Weak convergence methods for nonlinear partial differential equations. Regional conference series in mathematics vol. 74 (AMS, 1990).Google Scholar
13Florescu, L. C. and Godet-Thobie, C.. Young measures and compactness in metric spaces (De Gruyter, 2012).CrossRefGoogle Scholar
14Fonseca, I. and Leoni, G.. Modern methods in the calculus of variations: L p spaces, Springer Monographs in Mathematics (2007).Google Scholar
15Katzourakis, N.. L ∞-variational problems for maps and the Aronsson PDE system. J. Differ. Equat. 253 (2012), 2123–2139.CrossRefGoogle Scholar
16Katzourakis, N.. Explicit 2D ∞-Harmonic maps whose interfaces have junctions and corners. Comptes Rendus Acad. Sci. Paris, Ser. I 351 (2013), 677–680.CrossRefGoogle Scholar
17Katzourakis, N.. ∞-Minimal submanifolds. Proc. Am. Math. Soc. 142 (2014b), 2797–2811.CrossRefGoogle Scholar
18Katzourakis, N.. Optimal ∞-Quasiconformal immersions. ESAIM Control Optim. Calc. Var. 21 (2015b), 561–582.CrossRefGoogle Scholar
19Katzourakis, N.. An introduction to viscosity solutions for fully nonlinear PDE with applications to calculus of variations in L ∞, Springer Briefs in Mathematics (2015c), (doi: 10.1007/978-3-319-12829-0).CrossRefGoogle Scholar
20Katzourakis, N.. Generalised solutions for fully nonlinear PDE systems and existence-uniqueness theorems. J. Differ. Equat. 23 (2017a), 641–686 (doi: 10.1016/j.jde. 2017.02.048).CrossRefGoogle Scholar
21Katzourakis, N.. Absolutely minimising generalised solutions to the equations of vectorial calculus of variations in L ∞. Calc. Var. PDE 56 (2017b), 1–25 (doi: 10.1007/s00526-016-1099-z).CrossRefGoogle Scholar
22Katzourakis, N.. A new characterisation of ∞-harmonic and p-harmonic maps via affine variations in L ∞. Electron. J. Differ. Equat. 2017 (2017c), 1–19.Google Scholar
23Katzourakis, N. and Pryer, T.. On the numerical approximation of ∞-Harmonic mappings. Nonlin. Differ. Equ. Appl. 23 (2016), 1–23.CrossRefGoogle Scholar
24Katzourakis, N. and Pryer, T.. 2nd order L ∞ variational problems and the ∞-Polylaplacian, ArXiv preprint, http://arxiv.org/pdf/1605.07880.pdf.Google Scholar
25Kristensen, J. and Rindler, F.. Characterization of generalized gradient Young measures generated by sequences in W 1,1 and BV. Arch. Ration. Mech. Anal. 197 (2010), 539–598, and erratum Arch. Ration. Mech. Anal. 203, 693 - 700 (2012).CrossRefGoogle Scholar
26Pedregal, P.. Parametrized measures and variational principles (Birkhäuser, 1997).CrossRefGoogle Scholar
27Valadier, M.. Young measures, in ‘Methods of nonconvex analysis’. Lecture Notes in Mathematics, vol. 1446 pp. 152–188 (Springer, 1990).CrossRefGoogle Scholar