No CrossRef data available.
Published online by Cambridge University Press: 15 May 2023
We study anti-symmetric solutions about the hyperplane $\{x_n=0\}$ for the following fractional Hardy–Hénon system:
for the following fractional Hardy–Hénon system:
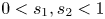 , $n>2\max \{s_1,s_2\}$
, $n>2\max \{s_1,s_2\}$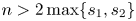 . Nonexistence of anti-symmetric solutions are obtained in some appropriate domains of $(p,q)$
. Nonexistence of anti-symmetric solutions are obtained in some appropriate domains of $(p,q)$ under some corresponding assumptions of $\alpha,\beta$
under some corresponding assumptions of $\alpha,\beta$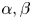 via the methods of moving spheres and moving planes. Particularly, for the case $s_1=s_2$
via the methods of moving spheres and moving planes. Particularly, for the case $s_1=s_2$ , one of our results shows that one domain of $(p,q)$
, one of our results shows that one domain of $(p,q)$ , where nonexistence of anti-symmetric solutions with appropriate decay conditions at infinity hold true, locates at above the fractional Sobolev's hyperbola under appropriate condition of $\alpha, \beta$
, where nonexistence of anti-symmetric solutions with appropriate decay conditions at infinity hold true, locates at above the fractional Sobolev's hyperbola under appropriate condition of $\alpha, \beta$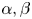 .
.