Hostname: page-component-669899f699-7tmb6 Total loading time: 0 Render date: 2025-04-27T13:53:28.986Z Has data issue: false hasContentIssue false
  • English
  • Français

Rigidity of capillary surfaces in compact 3-manifolds with strictly convex boundary

Part of: Classical differential geometry Global differential geometry

Published online by Cambridge University Press:  03 April 2023

Paulo Alexandre Sousa Open the ORCID record for Paulo Alexandre Sousa [Opens in a new window] ,
Rondinelle Marcolino Batista ,
Barnabé Pessoa Lima  and
Bruno Vasconcelos Mendes Vieira
Paulo Alexandre Sousa
Affiliation:
Departamento de Matemática, Universidade Federal do Piauí, Ininga - Teresina - PI 64049-550, Brazil ([email protected]; [email protected]; [email protected]; [email protected])
Rondinelle Marcolino Batista
Affiliation:
Departamento de Matemática, Universidade Federal do Piauí, Ininga - Teresina - PI 64049-550, Brazil ([email protected]; [email protected]; [email protected]; [email protected])
Barnabé Pessoa Lima
Affiliation:
Departamento de Matemática, Universidade Federal do Piauí, Ininga - Teresina - PI 64049-550, Brazil ([email protected]; [email protected]; [email protected]; [email protected])
Bruno Vasconcelos Mendes Vieira
Affiliation:
Departamento de Matemática, Universidade Federal do Piauí, Ininga - Teresina - PI 64049-550, Brazil ([email protected]; [email protected]; [email protected]; [email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper, we obtain one sharp estimate for the length 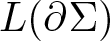$L(\partial\Sigma)$ of the boundary 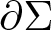$\partial\Sigma$ of a capillary minimal surface Σ2 in M3, where M is a compact three-manifolds with strictly convex boundary, assuming Σ has index one. The estimate is in term of the genus of Σ, the number of connected components of 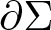$\partial\Sigma$ and the constant contact angle θ. Making an extra assumption on the geometry of M along 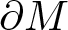$\partial M$, we characterize the global geometry of M, which is saturated only by the Euclidean three-balls. For capillary stable CMC surfaces, we also obtain similar results.

Keywords

capillary surfacesminimal surfacesconstant mean curvature surfacescompact three-manifoldsstrictly convex boundary

MSC classification

Primary: 53A10: Minimal surfaces, surfaces with prescribed mean curvature 53C42: Immersions (minimal, prescribed curvature, tight, etc.) 53C24: Rigidity results
Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 66 , Issue 1 , February 2023 , pp. 231 - 240
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press on Behalf of The Edinburgh Mathematical Society.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Brendle, S., A sharp bound for the area of minimal surfaces in the unit ball, Geom. Funct. Anal. 22(3) (2012), 621–626.10.1007/s00039-012-0167-6CrossRefGoogle Scholar
Fraser, A. and Li., M. M.-C., Compactness of the space of embedded minimal surfaces with free boundary in three-manifolds with nonnegative Ricci curvature and convex boundary, J. Differential Geom. 96(2) (2014), 183–200.10.4310/jdg/1393424916CrossRefGoogle Scholar
Gabard, A., Sur la représentation conforme des surfaces de Riemann à bord et une caractérisation des courbes séparantes, Comment. Math. Helv. 81(4) (2006), 945–964.10.4171/CMH/82CrossRefGoogle Scholar
Hang, F. and Wang, X., Rigidity theorems for compact manifolds with boundary and positive Ricci curvature, J. Geom. Anal. 19 (2009), 628–642.10.1007/s12220-009-9074-yCrossRefGoogle Scholar
Li, P., Schoen, R. and Yau, S.-T., On the isoperimetric inequality for minimal surfaces, Ann. Sc. Norm. Super. Pisa Cl. Sci. 11(2) (1984), 237–244.Google Scholar
Mendes, A., Rigidity of free boundary surfaces in compact 3-manifolds with strictly convex boundary, J. Geom. Anal. 28 (2018), 1245–1257.10.1007/s12220-017-9861-9CrossRefGoogle Scholar
Nitsche, J. C. C., Stationary partitioning of convex bodies, Arch. Ration. Mech. Anal. 89 (1985), 1–19.10.1007/BF00281743CrossRefGoogle Scholar
Nunes, I., On stable constant mean curvature surfaces with free boundary, Math. Z. 287 (2016), 473–479.10.1007/s00209-016-1832-5CrossRefGoogle Scholar
Ros, A., One-sided complete stable minimal surfaces, J. Differential Geom. 74(1) (2006), 69–92.10.4310/jdg/1175266182CrossRefGoogle Scholar
Ros, A., Stability of minimal and constant mean curvature surfaces with free boundary, Mat. Contemp. 35 (2008), 221–240.Google Scholar
Ros, A. and Souam, R., On stability of capillary surfaces in a ball, Pacific J. Math. 178(2) (1997), 345–361.10.2140/pjm.1997.178.345CrossRefGoogle Scholar
Ros, A. and Vergasta, E., Stability for hypersurfaces of constant mean curvature with free boundary, Geom. Dedicata 56 (1995), 19–33.10.1007/BF01263611CrossRefGoogle Scholar
Wang, G. and Xia, C., Uniqueness of stable capillary hypersurfaces in a ball, Math. Ann. 374 (2019), 1845–1882.10.1007/s00208-019-01845-0CrossRefGoogle Scholar
Xia, C., Rigidity of compact manifolds with boundary and nonnegative Ricci curvature, Proc. Amer. Math. Soc. 125(6) (1997), 1801–1806.10.1090/S0002-9939-97-04078-1CrossRefGoogle Scholar