Hostname: page-component-669899f699-tzmfd Total loading time: 0 Render date: 2025-04-28T23:24:37.556Z Has data issue: false hasContentIssue false
  • English
  • Français

Projectively and affinely invariant PDEs on hypersurfaces

Part of: General theory of differentiable manifolds Partial differential equations on manifolds; differential operators Global differential geometry Partial differential equations

Published online by Cambridge University Press:  25 April 2024

Dmitri Alekseevsky Open the ORCID record for Dmitri Alekseevsky [Opens in a new window] ,
Gianni Manno Open the ORCID record for Gianni Manno [Opens in a new window]  and
Giovanni Moreno Open the ORCID record for Giovanni Moreno [Opens in a new window]
Dmitri Alekseevsky
Affiliation:
Department of Algebra and Number Theory, Institute for Information Transmission Problems, Moscow, Russia Faculty of Science, University of Hradec Kralove, Hradec Kralove, Czech Republic
Gianni Manno*
Affiliation:
Dipartimento di Matematica ‘G. L. Lagrange’, Politecnico di Torino, Torino, Italy
Giovanni Moreno
Affiliation:
Department of Mathematical Methods in Physics, Faculty of Physics, University of Warsaw, Warszawa, Poland
*
Corresponding author: Gianni Manno, email: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

In Communications in Contemporary Mathematics 24 3, (2022),the authors have developed a method for constructing G-invariant partial differential equations (PDEs) imposed on hypersurfaces of an 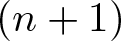$(n+1)$-dimensional homogeneous space 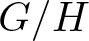$G/H$, under mild assumptions on the Lie group G. In the present paper, the method is applied to the case when 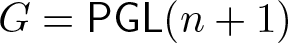$G=\mathsf{PGL}(n+1)$ (respectively, 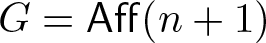$G=\mathsf{Aff}(n+1)$) and the homogeneous space 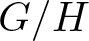$G/H$ is the 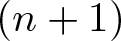$(n+1)$-dimensional projective 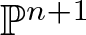$\mathbb{P}^{n+1}$ (respectively, affine 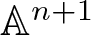$\mathbb{A}^{n+1}$) space, respectively. The main result of the paper is that projectively or affinely invariant PDEs with n independent and one unknown variables are in one-to-one correspondence with invariant hypersurfaces of the space of trace-free cubic forms in n variables with respect to the group 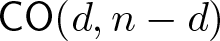$\mathsf{CO}(d,n-d)$ of conformal transformations of 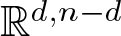$\mathbb{R}^{d,n-d}$.

Keywords

Homogeneous manifoldsLie symmetries of PDEsG-invariant PDEsJet spaces

MSC classification

Primary: 53C30: Homogeneous manifolds 58J70: Invariance and symmetry properties 35A30: Geometric theory, characteristics, transformations 58A20: Jets
Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 67 , Issue 3 , August 2024 , pp. 714 - 739
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press on Behalf of The Edinburgh Mathematical Society.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Alekseevsky, D. V., Gutt, J., Manno, G. and Moreno, G., A general method to construct invariant PDEs on homogeneous manifolds, Communications in Contemporary Mathematics 24(3) (2022), . doi:10.1142/s0219199720500893CrossRefGoogle Scholar
An-Min, L., Udo, S., Guosong, Z. and Zejun, H., Global Affine Differential Geometry of Hypersurfaces, Volume 11 of De Gruyter Expositions in Mathematics (Berlin: De Gruyter, 2015). doi:10.1515/9783110268898.Google Scholar
Blaschke, W., Vorlesungen über Differentialgeometrie und geometrische Grundlagen von Einsteins Relativitätstheorie II: Affine Differentialgeometrie (Grundlehren der mathematischen Wissenschaften) (German Edition), Volume 7 of Grundlehren der mathematischen Wissenschaften (Berlin - Heidelberg: Springer, 1923), https://www.xarg.org/ref/a/3642471250/.CrossRefGoogle Scholar
Cheng, S.-Y. and Yau, S.-T., Complete affine hypersurfaces. Part I. The completeness of affine metrics, Communications on Pure and Applied Mathematics 39(6) (1986), 839–866, doi:10.1002/cpa.3160390606.CrossRefGoogle Scholar
Ivey, T. A. and Landsberg, J. M., Cartan for Beginners: Differential Geometry via Moving Frames and Exterior Differential Systems, Volume 61 of Graduate Studies in Mathematics (American Mathematical Society, Providence, RI, 2003).Google Scholar
Krasil’shchik, I. S., Lychagin, V. V. and Vinogradov, A. M., Geometry of Jet Spaces and Nonlinear Partial Differential Equations, Volume 1 of Advanced studies in contemporary mathematics (New York- London- Paris - Montreux - Tokyo: Gordon and Breach, 1986).Google Scholar
Kushner, A., Lychagin, V. and Rubtsov, V., Contact Geometry and Non-Linear Differential Equations, Volume 101 of Encyclopedia of Mathematics and its Applications (Cambridge University Press, Cambridge, 2007).Google Scholar
Manno, D., Oliveri, F. and Vitolo, R., Differential equations uniquely determined by algebras of point symmetries, Teoret. Mat. Fiz. 151(3) (2007), 486–494. doi:10.1007/s11232-007-0069-1Google Scholar
Alekseevsky, D., Manno, G. and Moreno, G., Third-order affine and projective-invariant (systems of) PDEs in two independent variables as vanishing of the Fubini-Pick invariant, (2024), arXiv, https://arxiv.org/abs/2202.09894.Google Scholar
Onishchik, A. L. and Vinberg, E. B., Lie Group and Algebraic Groups, Springer Series in Soviet Mathematics (Springer, Berlin, Germany, 1990).CrossRefGoogle Scholar
Parshin, A. N. and Shafarevich, I. R., editors, Algebraic Geometry IV, Encyclopaedia of Mathematical Sciences, 1994 ed. (Springer, Berlin, Germany, 1994).CrossRefGoogle Scholar
Saunders, D. J., The Geometry of Jet Bundles, Volume 142 of London Mathematical Society Lecture Note Series (Cambridge University Press, Cambridge, 1989). doi:10.1017/CBO9780511526411CrossRefGoogle Scholar
Springer, T., Invariant Theory (Springer, Berlin, Germany, 1977).CrossRefGoogle Scholar
Yamaguchi, K., Contact geometry of higher order, Japan. J. Math. (N.S.) 8(1) (1982), 109–176.CrossRefGoogle Scholar