Hostname: page-component-669899f699-qzcqf Total loading time: 0 Render date: 2025-05-04T00:59:24.706Z Has data issue: false hasContentIssue false
  • English
  • Français

The planar 3-colorable subgroup ε of Thompson’s group F and its even part

Part of: Locally compact groups and their algebras Special aspects of infinite or finite groups

Published online by Cambridge University Press:  25 November 2024

Valeriano Aiello  and
Tatiana Nagnibeda
Valeriano Aiello*
Affiliation:
Dipartimento di Matematica, Università di Roma La Sapienza, Roma, Italy
Tatiana Nagnibeda
Affiliation:
Section de Mathématiques, Université de Genève, Genève, Switzerland
*
Corresponding author: Valeriano Aiello, email: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We study the planar 3-colorablesubgroup 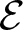$\mathcal{E}$ of Thompson’s group F and its even part 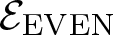${\mathcal{E}_{\rm EVEN}}$. The latter is obtained by cutting 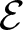$\mathcal{E}$ with a finite index subgroup of F isomorphic to F, namely the rectangular subgroup 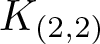$K_{(2,2)}$. We show that the even part 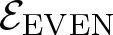${\mathcal{E}_{\rm EVEN}}$ of the planar 3-colorable subgroup admits a description in terms of stabilisers of suitable subsets of dyadic rationals. As a consequence 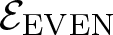${\mathcal{E}_{\rm EVEN}}$ is closed in the sense of Golan and Sapir. We then study three quasi-regular representations associated with 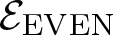${\mathcal{E}_{\rm EVEN}}$: two are shown to be irreducible and one to be reducible.

Keywords

Thompson groupstabiliser subgroupsquasi-regular representationsirreducible representationscoloringsJones’ actions

MSC classification

Primary: 20F65: Geometric group theory
Secondary: 22D10: Unitary representations of locally compact groups
Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 68 , Issue 1 , February 2025 , pp. 173 - 197
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press on Behalf of The Edinburgh Mathematical Society.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Aiello, V., On the Alexander theorem for the oriented Thompson group $\vec{F}$, Algebr. Geom. Topol. 20(1) (2020), 429–438, doi:10.2140/agt.2020.20.429.CrossRefGoogle Scholar
Aiello, V., An introduction to Thompson knot theory and to Jones subgroups, J. Knot Theory Ramifications (2022), preprint arXiv:2211.15461.Google Scholar
Aiello, V. and Baader, S., Arborescence of positive Thompson links, Pacific J. Math. 316(2) (2022), 237–248.CrossRefGoogle Scholar
Aiello, V. and Baader, S., Positive oriented Thompson links, Accepted for Publication in Communications in Analysis and Geometry. 32(6) (2024).Google Scholar
Aiello, V., Brothier, A. and Conti, R., Jones representations of Thompson’s group F arising from Temperley-Lieb-Jones algebras, Int. Math. Res. Not. 2021(15) (2021), 11209–11245. doi:10.1093/imrn/rnz240.CrossRefGoogle Scholar
Aiello, V. and Conti, R., Graph polynomials and link invariants as positive type functions on Thompson’s group F, J. Knot Theory Ramifications 28(2) (2019), . doi:10.1142/S0218216519500068.CrossRefGoogle Scholar
Aiello, V. and Conti, R., The Jones polynomial and functions of positive type on the oriented Jones-Thompson groups $\vec{F}$ and $\vec{T}$, Complex Anal. Oper. Theory 13(7) (2019), 3127–3149, doi:10.1007/s11785-018-0866-6.CrossRefGoogle Scholar
Aiello, V., Conti, R. and Jones, V. F. R., The Homflypt polynomial and the oriented Thompson group, Quantum Topol. 9(3) (2018), 461–472, doi:10.4171/QT/112.CrossRefGoogle Scholar
Aiello, V. and Jones, V. F. R., On spectral measures for certain unitary representations of R. Thompson’s group F, J. Funct. Anal. 280(1, 108777) (2021), , doi:10.1016/j.jfa.2020.108777.CrossRefGoogle Scholar
Aiello, V. and Nagnibeda, T., On the oriented Thompson subgroup $\vec{F}_3$ and its relatives in higher Brown-Thompson groups, J. Algebra Appl. 21(7) (2022), 1–21.CrossRefGoogle Scholar
Aiello, V. and Nagnibeda, T., On the 3-colorable subgroup $\mathcal{F}$ and maximal subgroups of Thompson’s group F, Annales l’Institut Fourier 73(2) (2023), 783–828, preprint arXiv:2103.07885.CrossRefGoogle Scholar
Araújo, F. and Pinto, P. R., Representations of Higman-Thompson groups from Cuntz algebras, J. Math. Anal. Appl. 509(2) (2022), .CrossRefGoogle Scholar
Barata, M. and Pinto, P. R., Representations of Thompson groups from Cuntz algebras, J. Math. Anal. Appl. 478(1) (2019), 212–228.CrossRefGoogle Scholar
Belk, J., Thompson’s group F, preprint arXiv:0708.3609, 2007.Google Scholar
Belk, J. and Matucci, F., Conjugacy and dynamics in Thompson’s groups, Geom. Dedicata 169 (2014), 239–261, doi:10.1007/s10711-013-9853-2.CrossRefGoogle Scholar
Bleak, C. and Wassink, B., Finite index subgroups of R, Thompson’s Group F (2007), 1–26.Google Scholar
Brothier, A. and Jones, V. F. R., Pythagorean representations of Thompson’s groups, J. Funct. Anal. 277(7) (2019), 2442–2469, doi:10.1016/j.jfa.2019.02.009.CrossRefGoogle Scholar
Brothier, A. and Jones, V. F. R., On the Haagerup and Kazhdan properties of R, Thompson’s groups, J. Group Theory 22(5) (2019), 795–807.CrossRefGoogle Scholar
Brothier, A. and Wijesena, D., Jones’ representations of R. Thompson’s groups not induced by finite-dimensional ones (2022), preprint arXiv:2211.08555.Google Scholar
Brown, K. S.. Finiteness properties of groups, J Pure Appl Algebra. 44(1–3) (1987), 45–75. doi:10.1016/0022-4049(87)90015-6.CrossRefGoogle Scholar
Burillo, J., Cleary, S. and Stein, M., Metrics and embeddings of generalizations of Thompson’s group F, Trans. Amer. Math. Soc. 353(4) (2001), 1677–1689.CrossRefGoogle Scholar
Cannon, J. W., Floyd, W. J. and Parry, W. R., Introductory notes on Richard Thompson’s groups, Enseign. Math. (2) 42(3–4) (1996), 215–256.Google Scholar
Francoeur, D., On the stabilisers of points in groups with micro-supported actions, J. Group Theory 24(3) (2021), 533–547.CrossRefGoogle Scholar
Golan Polak, G., Memoirs of the American Mathematical Society, (Providence, RI: American Mathematical Society (AMS), 2023).Google Scholar
Golan, G., On maximal subgroups of Thompson’s group F (2022), 1–62.Google Scholar
Golan, G. and Sapir, M., On Jones’ subgroup of R. Thompson group F, J. Algebra 470 (2017), 122–159, doi:10.1016/j.jalgebra.2016.09.001.CrossRefGoogle Scholar
Golan, G. and Sapir, M., On subgroups of R. Thompson’s group F, Trans. Amer. Math. Soc. 369(12) (2017), 8857–8878, doi:10.1090/tran/6982.CrossRefGoogle Scholar
Golan, G. and Sapir, M., On the stabilizers of finite sets of numbers in the R. Thompson group F, Algebra i Analiz, 29(1) (2017), 70–110, doi:10.1090/spmj/1482.Google Scholar
Golan, G. and Sapir, M., On Closed Subgroups of the R (Thompson group F, 2021), preprint arXiv:2105.00531.Google Scholar
Grymski, A. and Peters, E., Conway rational tangles and the Thompson group (2022), 1–23.Google Scholar
Jones, V. F. R., Some unitary representations of Thompson’s groups F and T, J. Comb. Algebra 1(1) (2017), 1–44, doi:10.4171/JCA/1-1-1.CrossRefGoogle Scholar
Jones, V. F. R., A no-go theorem for the continuum limit of a periodic quantum spin chain, Comm. Math. Phys. 357(1) (2018), 295–317, doi:10.1007/s00220-017-2945-3.CrossRefGoogle Scholar
Jones, V. F. R., Irreducibility of the Wysiwyg representations of Thompson’s groups, Representation Theory, Mathematical Physics, and Integrable Systems 340 (2021), 411–430.CrossRefGoogle Scholar
Jones, V. F. R., Planar algebras, New Zealand J. Math. 52 (2021), 1–107, preprint arXiv:9909027.CrossRefGoogle Scholar
Mackey, G. W., The Theory of Unitary Group Representations, (University of Chicago, Chicago Lectures in Mathematics, 1976) 1955.Google Scholar
Morrison, S., Peters, E. and Snyder, N., Categories generated by a trivalent vertex, Selecta Math. (N.S.) 23(2) (2017), 817–868, doi:10.1007/s00029-016-0240-3.CrossRefGoogle Scholar
Ren, Y., From skein theory to presentations for Thompson group, J. Algebra 498 (2018), 178–196, doi:10.1016/j.jalgebra.2017.11.018.CrossRefGoogle Scholar
Savchuk, D., Some Graphs Related to Thompson’s Group F, Combinatorial and Geometric Group Theory (, 2010). Basel: Birkhäuser. doi:10.1007/978-3-7643-9911-5_12.Google Scholar
Savchuk, D., Schreier graphs of actions of Thompson’s group F on the unit interval and on the Cantor set, Geom. Dedicata 175 (2015), 355–372, doi:10.1007/s10711-014-9951-9.CrossRefGoogle Scholar