Hostname: page-component-669899f699-chc8l Total loading time: 0 Render date: 2025-04-28T00:01:16.009Z Has data issue: false hasContentIssue false
  • English
  • Français

Model structures, n-Gorenstein flat modules and PGF dimensions

Part of: Harmonic analysis in several variables Homological methods

Published online by Cambridge University Press:  22 November 2024

Rachid El Maaouy Open the ORCID record for Rachid El Maaouy [Opens in a new window]
Rachid El Maaouy*
Affiliation:
CeReMaR Research Center, Faculty of Sciences, Mohammed V University in Rabat, Rabat, Morocco
*
Email: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Given a non-negative integer n and a ring R with identity, we construct a hereditary abelian model structure on the category of left R-modules where the class of cofibrant objects coincides with 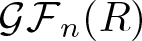$\mathcal{GF}_n(R)$ the class of left R-modules with Gorenstein flat dimension at most n, the class of fibrant objects coincides with 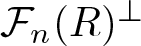$\mathcal{F}_n(R)^\perp$ the right ${\rm Ext}$-orthogonal class of left R-modules with flat dimension at most n, and the class of trivial objects coincides with 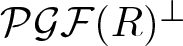$\mathcal{PGF}(R)^\perp$ the right ${\rm Ext}$-orthogonal class of PGF left R-modules recently introduced by Šaroch and . The homotopy category of this model structure is triangulated equivalent to the stable category 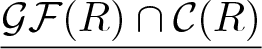$\underline{\mathcal{GF}(R)\cap\mathcal{C}(R)}$ modulo flat-cotorsion modules and it is compactly generated when R has finite global Gorenstein projective dimension.

The second part of this paper deals with the PGF dimension of modules and rings. Our results suggest that this dimension could serve as an alternative definition of the Gorenstein projective dimension. We show, among other things, that (n-)perfect rings can be characterized in terms of Gorenstein homological dimensions, similar to the classical ones, and the global Gorenstein projective dimension coincides with the global PGF dimension.

Keywords

abelian model structure(projectively coresolved) Gorenstein flat modules and dimensionsglobal Gorenstein projective dimensions

MSC classification

Primary: 42B25: Maximal functions, Littlewood-Paley theory 16E10: Homological dimension 16E65: Homological conditions on rings (generalizations of regular, Gorenstein, Cohen-Macaulay rings, etc.)
Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 67 , Issue 4 , November 2024 , pp. 1241 - 1264
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press on Behalf of The Edinburgh Mathematical Society.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Adámek, J. and Rosický, J., Locally presentable and accessible categories. Number 189 in London Mathematical Society Lecture Note Series (Cambridge University Press, 1994).Google Scholar
Bennis, D., El Maaouy, R., García Rozas, J. R. and Oyonarte, L., Relative Gorenstein flat modules and dimension, Comm. Alg. 126(2) (2025), 349–367.Google Scholar
Bennis, D., El Maaouy, R., García Rozas, J. R. and Oyonarte, L., Relative Gorenstein Flat Modules and Foxby Classes and Their Model Structures, J. Algebra Appl. (2024), . doi:10.1142/S0219498825501944CrossRefGoogle Scholar
Bennis, D., Hu, K. and Wang, F., Gorenstein analogue of Auslander’s theorem on the global dimension, Comm. Alg. 43(1) (2015), 174–181.CrossRefGoogle Scholar
Bennis, D. and Mahdou, N., Strongly Gorenstein projective, injective, and flat modules, J. Pure Appl. Algebra. 210(2) (2007), 437–445.CrossRefGoogle Scholar
Bennis, D. and Mahdou, N., Global Gorenstein dimensions, Proc. Am. Math. Soc. 138(2) (2010), 461–465.CrossRefGoogle Scholar
Bravo, D., Gillespie, J. and Hovey, M., (2014) https://arxiv.org/abs/1405.5768.Google Scholar
Bravo, D., Gillespie, J. and Hovey, M., The Stable Module Category of a General Ring (2014) https://arxiv.org/abs/1405.5768.Google Scholar
Cortés-Izurdiaga, M., Products of flat modules and global dimension relative to $\mathcal{F}$-Mittag-Leffler modules, Proc. Amer. Math. Soc. 144(11) (2016), 4557–4571.CrossRefGoogle Scholar
Cortés-Izurdiaga, M. and Saroch, J., Module classes induced by complexes and λ-pure-injective modules. arXiv:2104.08602 (2021).Google Scholar
Dalezios, G. and Emmanouil, I., Homological dimension based on a class of Gorenstein flat modules. (2022) arXiv: 2208.05692.Google Scholar
Ding, N., Li, Y. and Mao, L., Strongly Gorenstein flat modules, J. Aust. Math. Soc. 66(3) (2009), 323–338.CrossRefGoogle Scholar
Ding, N. and Mao, L., Envelopes and covers by modules of finite FP-injective and flat dimensions, Comm. Alg. 35(3) (2007), 833–849.Google Scholar
Emmanouil, I., On the finiteness of Gorenstein homological dimensions, J. Algebra. 372 (2012), 376–396.CrossRefGoogle Scholar
Enochs, E. and Jenda, O., Relative Homological Algebra. de Gruyter Expositions in Mathematics, Volume 30 (Walter de Gruyter, 2000).CrossRefGoogle Scholar
Enochs, E., Jenda, O. and López-Ramos, J. A., Dualizing modules and n-perfect rings, Proc. Edinburgh Math. Soc. 48(1) (2005), 75–90.CrossRefGoogle Scholar
Estrada, S. and Gillespie, J., The projective stable category of a coherent scheme, Proc. R. Soc. Edinb. Sect. A, Math. 149(1) (2019), 15–43.CrossRefGoogle Scholar
Estrada, S., Iacob, A. and Pérez, M. A., Model structures and relative Gorenstein flat modules and chain complexes. Categorical, Homological and Combinatorial Methods in Algebra, Volume 751 (2020), .Google Scholar
Göbel, R. and Trlifaj, J., Approximations and Endomorphism Algebras of Modules, 2nd revised and extended edition, 41 (Berlin, Boston: De Gruyter, 2012).CrossRefGoogle Scholar
Gillespie, J., Model structures on modules over Ding-Chen rings, Homology Homotopy Appl. 12(1) (2010), 61–73.CrossRefGoogle Scholar
Gillespie, J., Model structures on exact categories, J. Pure. Appl. Algebra. 215(12) (2011), 2892–2902.CrossRefGoogle Scholar
Gillespie, J., Hereditary abelian model categories, Bull. Lond. Math. Soc. 48(6) (2016), 895–922.CrossRefGoogle Scholar
Hovey, M., Model Categories, Volume 63 (American Mathematical Society, Providence, RI, 1999) Mathematical Surveys and Monographs.Google Scholar
Hovey, M., Cotorsion pairs, model category structures, and representation theory, Math. Z. 241(3) (2002), 553–592.CrossRefGoogle Scholar
Huang, Z., Homological dimensions relative to preresolving subcategories II, Forum Math. 34(2) (2022), 507–530.CrossRefGoogle Scholar
Huerta, M. Y., Mendoza, O. and Pérez, M. A., m-periodic Gorenstein objects, J. Algebra. 621 (2023), 1–40.CrossRefGoogle Scholar
Huerta, M. Y., Mendoza, O. and Pérez, M. A., Corrigendum to “m-Periodic Gorenstein objects” [J. Algebra 621 (2023) 1–40], J. Algebra 654 (2024), 70–81.CrossRefGoogle Scholar
Iacob, A., Projectively coresolved Gorenstein flat and ding projective modules, Comm. Alg. 48(7) (2020), 2883–2893.CrossRefGoogle Scholar
Liang, L. and Wang, J., Relative global dimensions and stable homotopy categories, C. R. Math. Acad. Sci. Paris. 358(3) (2020), 379–392.CrossRefGoogle Scholar
Pérez, M. A., Introduction to Abelian model structures and Gorenstein homological dimensions. Monographs and Research Notes in Mathematics (CRC Press, Boca Raton, FL, 2016).Google Scholar
Prest, M., Purity, spectra and localisation. Of Encyclopedia of Mathematics and its Applications, Volume 121 (Cambridge University Press, Cambridge, 2009).Google Scholar
Saroch, J. and Stovicek, J., Singular compactness and definability for Σ-cotorsion and Gorenstein modules, Selecta Math. 26(2) (2020), 23–40.CrossRefGoogle Scholar
Stergiopoulou, D. D., Strongly n-projectively coresolved Gorenstein flat modules. (2022), arXiv:2210.16816.Google Scholar
Wang, J., Yang, G., Shao, Q. and Zhang, Q., On Gorenstein global and Gorenstein weak global dimensions, Colloq. Math. 174 (2023), 45–67.CrossRefGoogle Scholar
Xu, A., Gorenstein modules and Gorenstein model structures, Glasg. Math. J. 59(3) (2017), 1–19.CrossRefGoogle Scholar
Yang, G. and Liu, Z., Gorenstein flat covers over GF-closed rings, Commun. Alg. 40(5) (2012), 1632–1640.Google Scholar