Hostname: page-component-669899f699-rg895 Total loading time: 0 Render date: 2025-04-28T19:23:42.015Z Has data issue: false hasContentIssue false
  • English
  • Français

Ideals of equations for elements in a free group and Stallings folding

Part of: Structure and classification of infinite or finite groups Special aspects of infinite or finite groups

Published online by Cambridge University Press:  19 December 2024

Dario Ascari Open the ORCID record for Dario Ascari [Opens in a new window]
Dario Ascari*
Affiliation:
Department of Mathematics, University of the Basque Country, Leioa, Biscay, Spain
*
Email: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 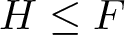$H\le F$ be two finitely generated free groups. Given 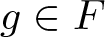$g\in F$, we study the ideal 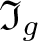$\mathfrak I_g$ of equations for g with coefficients in H, i.e. the elements 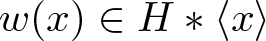$w(x)\in H*\langle x\rangle$ such that 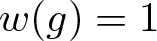$w(g)=1$ in F. The ideal 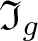$\mathfrak I_g$ is a normal subgroup of 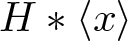$H*\langle x\rangle$, and it’s possible to algorithmically compute a finite normal generating set for 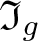$\mathfrak I_g$; we give a description of one such algorithm, based on Stallings folding operations. We provide an algorithm to find an equation in w(x)\in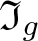$\mathfrak I_g$ with minimum degree, i.e.  such that its cyclic reduction contains the minimum possible number of occurrences of x and x−1; this answers a question of A. Rosenmann and E. Ventura. More generally, we show how to algorithmically compute the set Dg of all integers d such that 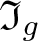$\mathfrak I_g$ contains equations of degree d; we show that Dg coincides, up to a finite set, with either 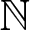$\mathbb N$ or 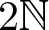$2\mathbb N$. Finally, we provide examples to illustrate the techniques introduced in this paper. We discuss the case where 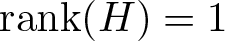${\text{rank}}(H)=1$. We prove that both kinds of sets Dg can actually occur. We show that the equations of minimum possible degree aren’t in general enough to generate the whole ideal 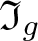$\mathfrak I_g$ as a normal subgroup.

Keywords

geometric group theoryfree groupsequations over groupsStallings automataalgorithms in group theory

MSC classification

Primary: 20F70: Algebraic geometry over groups; equations over groups
Secondary: 20E05: Free nonabelian groups 20F65: Geometric group theory
Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , First View , pp. 1 - 42
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press on Behalf of The Edinburgh Mathematical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Ascari, D.. Ideals of equations for elements in a free group and context-free languages, arXiv:2211.10276, (2022).CrossRefGoogle Scholar
Delgado, J. and Ventura, E.. A list of applications of Stallings automata, https://arxiv.org/abs/2109.01268, (2022).Google Scholar
Delgado, J. and Ventura, E.. Stallings automata, https://arxiv.org/abs/2403.10757, (2024).Google Scholar
Feighn, M. and Handel, M., Mapping tori of free group automorphisms are coherent, Ann. Math. 149(3) (1999), 1061–1077.CrossRefGoogle Scholar
Kapovich, I. and Myasnikov, A., Stallings foldings and subgroups of free groups, J. Algebra 248(2) (2002), 608–668.CrossRefGoogle Scholar
Kapovich, I., Myasnikov, A. and Weidmann, R., Foldings, graphs of groups and the membership problem, Internat. J. Algebra Comput. 15(1) (2005), 95–128.CrossRefGoogle Scholar
Lyndon, R. C. and Schupp, P. E., Combinatorial Group Theory. Classics in Mathematics, (Springer-Verlag, Berlin, 2001). Reprint of the 1977 edition.CrossRefGoogle Scholar
Magnus, W., Untersuchungen über einige unendliche diskontinuierliche Gruppen, Ann. Math. 105(1-3) (1931), 52–74.CrossRefGoogle Scholar
Margolis, S., Sapir, M. and Weil, P., Closed subgroups in pro-V topologies and the extension problem for inverse automata, Internat. J. Algebra Comput. 11(4) (2001), 405–445.CrossRefGoogle Scholar
Miasnikov, A., Ventura, E. and Weil, P., Algebraic extensions in free groups. In Geometric Group Theory, (Birkhäuser, Basel, 2007).Google Scholar
Muller, D. E. and Schupp, P. E., Groups, the theory of ends, and context-free languages, J. Comput. System Sci. 26(3) (1983), 295–310.CrossRefGoogle Scholar
Puder, D., Primitive words, free factors and measure preservation, Israel J. Math. 201(1) (2014), 25–73.CrossRefGoogle Scholar
Rosenmann, A., On rank, root and equations in free groups, Internat. J. Algebra Comput. 11(3) (2001), 375–390.CrossRefGoogle Scholar
Rosenmann, A. and Ventura, E.. Dependence over subgroups of free groups (version v2), 2023, https://arxiv.org/abs/2107.03154.Google Scholar
Serre, J.P.. Arbres, Amalgames, Sl2. Asterisque, Tome 46. Soc. Math. De France, 1977.Google Scholar
Silva, P. V. and Weil, P., On an algorithm to decide whether a free group is a free factor of another, RAIRO Theor. Inform. Appl. 42(2) (2007), 395–414.CrossRefGoogle Scholar
Silva, P. V. and Weil, P., On finite-index extensions of subgroups of free groups, J. Group Theory 13(3) (2010), 365–381.CrossRefGoogle Scholar
Stallings, J. R., Topology of finite graphs, Invent. Math. 71(3) (1983), 551–565.CrossRefGoogle Scholar
Takahasi, M., Note on chain conditions in free groups, Osaka J. Math. 3(2) (1951), 221–225.Google Scholar
Ventura, E., On fixed subgroups of maximal rank, Comm. Algebra 25(10) (1997), 3361–3375.CrossRefGoogle Scholar