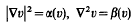Hostname: page-component-669899f699-b58lm Total loading time: 0 Render date: 2025-04-27T16:58:20.617Z Has data issue: false hasContentIssue false
  • English
  • Français

Geometrical aspects of the system and applications to the nonlinear wave equation

Published online by Cambridge University Press:  20 January 2009

G. Cieciura  and
A. M. Grundland
G. Cieciura
Affiliation:
Institute of Mathematical Methods in Physics, Warsaw Univeristy, HOZA 74 St, 00-682 Warsaw, Poland
A. M. Grundland
Affiliation:
Department of Mathematics and Statistics, Memorial University of Newfoundland, St John's, Newfoundland, Canada, A1C 5S7
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let E be n-dimensional (n≧2) real vector space with a nondegenerate symmetric scalar product (.|.):E × E → R1 with an arbitrary signature (p, n–p). Let us consider a second order partial differential equation (P.D.E.) of the form:

where φ is a given function of two variables, v is an unknown function (defined on an open subset 0 ⊂E), |∇ν|2: =(∇ν|∇ν) is the square of the gradient ∇ν of the function ν and ∇2, denotes the Laplace-Beltrami operator.

Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 30 , Issue 2 , June 1987 , pp. 247 - 256
Copyright
Copyright © Edinburgh Mathematical Society 1987

References

REFERENCES

1.Cieciura, G. and Grundland, A. M., A certain class of solutions of the non-linear wave equations, J. Math. Phys. 25 (1984), 3460–3469.CrossRefGoogle Scholar
2.Collins, C. B., All solutions to a nonlinear system of complex potential equations, J. Math. Phys. 21 (1980), 240–248.CrossRefGoogle Scholar
3.Collins, C. B., Complex equations, special relativity and complex Minkowski space-time, J. Math. Phys. 21 (1980), 249–255.CrossRefGoogle Scholar
4.Grundland, A. M., Harnad, J. and Winternitz, P., Solutions of the multidimensional Sine-Gordon equation obtained by symmetry reduction, Kinam. Rev. Fis. 4 (1982), 333–344.Google Scholar
5.Hermann, R., Differential Geometry and the Calculus of Variations (Math. Sci. Press, Brookline, Massachusetts, 1977).Google Scholar
6.Berestycki, H. and Lions, P. L., Existence of stationary states in nonlinear scalar field equation, in Bardos, C. and Bessis, D. (eds.), Bifurcation Phenomena in Mathematical Physics and Related Topics (D. Reidel Publ. Comp., New York, 1980).Google Scholar
7.Lang, S., Algebra (Addison-Wesley Publ. Comp., London, 1970).Google Scholar
8.Kobayashi, S. and Nomizu, K., Foundations of Differential Geometry, Vols. I and II (J. Wiley-Interscience, New York, 1962).Google Scholar
9.Sternberg, S., Lectures on Differential Geometry (Prentice-Hall, Englewood Cliffs, NY, 1964).Google Scholar
10.Peradzynski, Z., Riemann invariants for the nonplanar k-waves, Bull. Acad. Polon. Sci. Ser. Tech. 19 (1971), 67–74.Google Scholar
11.Emden, R., Gaskugeln (Berlin and Leipzig, 1907).Google Scholar
12.Davis, H., Introduction to Nonlinear Differential and Integral Equations (Dover, New York, 1960).Google Scholar