Hostname: page-component-669899f699-vbsjw Total loading time: 0 Render date: 2025-04-29T00:09:39.743Z Has data issue: false hasContentIssue false
  • English
  • Français

Existence and non-existence results for a class of systems under concave-convex nonlinearities

Part of: Partial differential equations Elliptic equations and systems

Published online by Cambridge University Press:  22 November 2024

João Pablo Pinheiro Da Silva Open the ORCID record for João Pablo Pinheiro Da Silva [Opens in a new window]
João Pablo Pinheiro Da Silva*
Affiliation:
Universidade Federal do Pará, Departamento de Matemática, Belém, Pará, Brazil
*
Email: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

In this work, we are interested in studying the following class of problems:(𝒫λμ)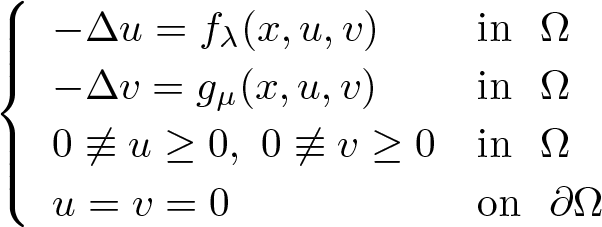

\begin{align}\left\{\begin{array}{ll}-\Delta u=f_\lambda(x,u,v)& \text{in}~~\Omega\\-\Delta v=g_\mu(x,u,v) & \text{in}~~\Omega\\0\not\equiv u\geq 0,\,\,0\not\equiv v\geq 0& \text{in}~~\Omega\\u=v=0&\text{on}~~\partial\Omega\end{array}\right.\end{align}
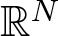where Ω is a bounded domain in $\mathbb{R}^N$, λ > 0, µ > 0, 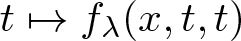$t\mapsto f_\lambda(x,t,t)$ and 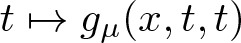$t\mapsto g_\mu(x,t,t)$ have concave-convex type nonlinearities. We present results related to the existence and non-existence of solutions for problem $(\mathcal{P}_{\lambda\mu})$.

Keywords

sub-super solutionnon-existence for systemsconcave-convex nonlinearities

MSC classification

Primary: 35A01: Existence problems 35B09: Positive solutions 35J47: Second-order elliptic systems
Secondary: 35A16: Topological and monotonicity methods
Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 68 , Issue 1 , February 2025 , pp. 128 - 156
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press on Behalf of The Edinburgh Mathematical Society.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Adriouch, K. and El Hamidi, A., The Nehari manifold for systems of nonlinear elliptic equations, Nonlinear Anal. 64(10) (2006), 2149–2167.CrossRefGoogle Scholar
Afrouzi, G. A. and Rasouli, S. H., A remark on the existence of multiple solutions to a multiparameter nonlinear elliptic system, Nonlinear Anal. 71(1–2) (2009), 445–455.CrossRefGoogle Scholar
Albalawi, W., Mercuri, C. and Moroz, V., Groundstate asymptotics for a class of singularly perturbed p-Laplacian problems in $\mathbb{R}^N$, Ann. Mat. Pura Appl. (4) 199(1) (2020), 23–63.CrossRefGoogle Scholar
Ambrosetti, A., Brézis, H. and Cerami, G., Combined effects of concave and convex nonlinearities in some elliptic problems, J. Funct. Anal. 122(2) (1994), 519–543.CrossRefGoogle Scholar
Arcoya, D., Boccardo, L. and Orsina, L., Critical points for functionals with quasilinear singular Euler-Lagrange equations, Calc. Var. Partial Differential Equations 47(1–2) (2013), 159–180.CrossRefGoogle Scholar
Barrios, B., Colorado, E., De Pablo, A. and Sánchez, U., On some critical problems for the fractional Laplacian operator, J. Differential Equations 252(11) (2012), 6133–6162.CrossRefGoogle Scholar
Barrios, B., Colorado, E., Servadei, R. and Soria, F., A critical fractional equation with concave-convex power nonlinearities, Ann. Inst. H. Poincaré Anal. Non LinéAire 32(4) (2015), 875–900.CrossRefGoogle Scholar
Bartsch, T. and Willem, M., On an elliptic equation with concave and convex nonlinearities, Proc. Amer. Math. Soc. 123(11) (1995), 3555–3561.CrossRefGoogle Scholar
Batkam, C. J. and Colin, F., The effects of concave and convex nonlinearities in some noncooperative elliptic systems, Ann. Mat. Pura Appl. (4) 193(6) (2014), 1565–1576.CrossRefGoogle Scholar
Brändle, C., Colorado, E., De Pablo, A. and Sánchez, U., A concave-convex elliptic problem involving the fractional Laplacian, Proc. Roy. Soc. Edinburgh Sect. A 143(1) (2013), 39–71CrossRefGoogle Scholar
Brézis, H., Functional Analysis, Sobolev Spaces and Partial Differential Equations, (Universitext. Springer, New York, 2011).CrossRefGoogle Scholar
Brézis, H. and Nirenberg, L., Positive solutions of nonlinear elliptic equations involving critical Sobolev exponents, Comm. Pure Appl. Math. 36 (4) (1983), 437–477.CrossRefGoogle Scholar
Brézis, H. and Oswald, L., Remarks on sublinear elliptic equations, Nonlinear Anal. 10(1) (1986), 55–64.CrossRefGoogle Scholar
Brown, K. J. and Wu, T. F., A semilinear elliptic system involving nonlinear boundary condition and sign-changing weight function, J. Math. Anal. Appl. 337(2) (2008), 1326–1336.CrossRefGoogle Scholar
Candela, A. M., Palmieri, G. and Salvatore, A., Multiple solutions for some symmetric supercritical problems, Commun. Contemp. Math. 22(8) (2020), , 1950075.CrossRefGoogle Scholar
Candela, A. M., Perera, K. and Sportelli, C., On a class of supercritical N-Laplacian problems, Nonlinear Anal. Real World Appl. 71 (2023), , Paper No. 103817.CrossRefGoogle Scholar
Candela, A. M. and Sportelli, C., Multiple solutions for coupled gradient-type quasilinear elliptic systems with supercritical growth, Ann. Mat. Pura Appl. (4) 201(5) (2022), 2341–2369.CrossRefGoogle Scholar
Chen, W. and Deng, S., Multiple solutions for a critical fractional elliptic system involving concave-convex nonlinearities, Proc. Roy. Soc. Edinburgh Sect. A 146(6) (2016), 1167–1193.CrossRefGoogle Scholar
Cheng, X., Feng, Z. and Wei, L., Nontrivial solutions for a quasilinear elliptic system with weight functions, Differential Integral Equations 33(11–12) (2020), 625–656.CrossRefGoogle Scholar
Chhetri, M., Raynor, S. and Robinson, S., On the existence of multiple positive solutions to some superlinear systems, Proc. Roy. Soc. Edinburgh Sect. A 142(1) (2012), 39–59.CrossRefGoogle Scholar
Clapp, M. and Tiwari, S., Multiple solutions to a pure supercritical problem for the p-Laplacian, Calc. Var. Partial Differ. Equ. 55(1) (2016), , Art. 7.CrossRefGoogle Scholar
Da Silva, J. P. P., Existence of non-negative solutions for a system with concave-convex nonlinearity, J. Elliptic Parabol. Equ. 9(2) (2023), 1319–1328.CrossRefGoogle Scholar
Da Silva, J. P. P., Global and local results for a gradient system with concave-convex nonlinearities. Preprint.Google Scholar
Da Silva, J. P. P., $W_0^{1,p}(\Omega)\times W_0^{1,p}(\Omega)$ versus $C_0^1 (\Omega)\times C_0^1(\Omega)$ local minimizers, Asymptotic Analysis 140(1–2), 59–76. doi: 10.3233/ASY-241911.Google Scholar
De Figueiredo, D. G., Gossez, J. P. and Ubilla, P., Local superlinearity and sublinearity for indefinite semilinear elliptic problems, J. Funct. Anal. 199(2) (2003), 452–467.CrossRefGoogle Scholar
De Figueiredo, D. G., Gossez, J. P. and Ubilla, P., Multiplicity results for a family of semilinear elliptic problems under local superlinearity and sublinearity, J. Eur. Math. Soc. (JEMS) 8(2) (2006), 269–286.CrossRefGoogle Scholar
De Paiva, F. O., Nonnegative solutions of elliptic problems with sublinear indefinite nonlinearity, J. Funct. Anal. 261(9) (2011), 2569–2586.CrossRefGoogle Scholar
García-Azorero, J. and Peral, I., Some results about the existence of a second positive solution in a quasilinear critical problem, Indiana Univ. Math. J. 43(3) (1994), 941–957.CrossRefGoogle Scholar
García-Azorero, J., Peral, I. and Manfredi, J. J., Sobolev versus Hölder local minimizers and global multiplicity for some quasilinear elliptic equations, Commun. Contemp. Math. 2(3) (2000), 385–404.CrossRefGoogle Scholar
García-Azorero, J., Peral, I. and Rossi, J. D., A convex-concave problem with a nonlinear boundary condition, J. Differential Equations 198(1) (2004), 91–128.CrossRefGoogle Scholar
Gilbarg, D. and Trudinger, N., Elliptic Partial Differential Equations of Second Order, Classics Math. (Springer-Verlag, Berlin, 2001) reprint of the 1998 edition.CrossRefGoogle Scholar
He, X., Squassina, M. and Zou, W., The Nehari manifold for fractional systems involving critical nonlinearities, Commun. Pure Appl. Anal. 15(4) (2016), 1285–1308.CrossRefGoogle Scholar
Hess, P. and Kato, T., On some linear and nonlinear eigenvalue problems with an indefinite weight function, Comm. Partial Differ. Equ. 5(10) (1980), 999–1030.CrossRefGoogle Scholar
Hirano, N., Saccon, C. and Shioji, N., Existence of multiple positive solutions for singular elliptic problems with concave and convex nonlinearities, Adv. Differ. Equ. 9(1–2) (2004), 197–220.Google Scholar
Hopf, E.. Elementare Bemerkungen über die Lösung partieller Differentialgleichungen zweiter Ordnung vom elliptischen Typus, Sitzungber. Preuss. Akad. Wiss. Phys. Math. Kl. 19: (1927), 147–152.Google Scholar
Hsu, T. S., Multiple positive solutions for a critical quasilinear elliptic system with concave-convex nonlinearities, Nonlinear Anal. 71(7–8) (2009), 2688–2698.CrossRefGoogle Scholar
Krein, M. G. and Rutman, M. A., Linear operators leaving invariant a cone in a Banach space, Uspekhi Mat. Nauk 3(1) (1948), 3–95.Google Scholar
Li, Q. and Yang, Z., Multiplicity of positive solutions for a p-q-Laplacian system with concave and critical nonlinearities, J. Math. Anal. Appl. 423(1) (2015), 660–680.CrossRefGoogle Scholar
Marano, S. A. and Papageorgiou, N. S., Positive solutions to a Dirichlet problem with p-Laplacian and concave-convex nonlinearity depending on a parameter, Commun. Pure Appl. Anal. 12(2) (2013), 815–829.CrossRefGoogle Scholar
Rabinowitz, P. H.Theorie du degré topologique et applications à des problèmes aux limites non linéaires. Lect. Notes, Analyse Numérique Fonctionnelle, Univ. Paris VI. (1975)Google Scholar
Rasouli, S. and Afrouzi, G. A., The Nehari manifold for a class of concave-convex elliptic systems involving the p-Laplacian and nonlinear boundary condition, Nonlinear Anal. 73(10) (2010), 3390–3401.CrossRefGoogle Scholar
Song, H., Chen, C. and Yan, Q., Existence of multiple solutions for a p-Laplacian system in RN with sign-changing weight functions, Canad. Math. Bull. 59(2) (2016), 417–434.CrossRefGoogle Scholar
Struwe, M., Variational methods. Applications to nonlinear partial differential equations and Hamiltonian systems. Ergebnisse der Mathematik und Ihrer Grenzgebiete (3) [Results in Mathematics and Related Areas (3)], 2nd edn, Volume 34, pp. (Springer-Verlag, Berlin, 1996).Google Scholar
Tang, M., Exact multiplicity for semilinear elliptic Dirichlet problems involving concave and convex nonlinearities, Proc. Roy. Soc. Edinburgh Sect. A 133(3) (2003), 705–717.CrossRefGoogle Scholar
Wang, Z. Q., Nonlinear boundary value problems with concave nonlinearities near the origin, NoDEA Nonlinear Differ. Equ. Appl. 8(1) (2001), 15–33.CrossRefGoogle Scholar
Wu, T. F., The Nehari manifold for a semilinear elliptic system involving sign-changing weight functions, Nonlinear Anal. 68(6) (2008), 1733–1745.CrossRefGoogle Scholar
Wu, T. F., Multiple positive solutions for a class of concave-convex elliptic problems in $\mathbb{R}^N$ involving sign-changing weight, J. Funct. Anal. 258(1) (2010), 99–131.CrossRefGoogle Scholar
Yin, H., Existence of multiple positive solutions for a p-q-Laplacian system with critical nonlinearities, J. Math. Anal. Appl. 403(1) (2013), 200–214.CrossRefGoogle Scholar