Hostname: page-component-669899f699-8p65j Total loading time: 0 Render date: 2025-05-05T15:27:28.350Z Has data issue: false hasContentIssue false
  • English
  • Français

Equisingularity in pencils of curves on germs of reduced complex surfaces

Part of: Local theory

Published online by Cambridge University Press:  04 June 2024

Gonzalo Barranco Mendoza  and
Jawad Snoussi
Gonzalo Barranco Mendoza*
Affiliation:
Universidad Nacional Autónoma de México, Instituto de Matemáticas, Unidad Cuernavaca, Morelos, Mexico
*
Corresponding author: Gonzalo Barranco Mendoza, email: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We study pencils of curves on a germ of complex reduced surface 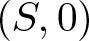$(S,0)$. These are families of curves parametrized by 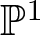$ \mathbb{P}^1 $ having 0 as the unique common point. We prove that for 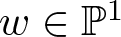$w\in \mathbb{P}^1$, the corresponding curve of the pencil does not have the generic topology if and only if either the corresponding curve of the pulled-back pencil to the normalized surface has a non generic topology or w is a limit value for the function 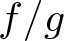$ f/g $ along the singular locus of 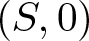$(S,0)$, where f and g are generators of the pencil.

Keywords

surface singularitiespencils of curvesequisingularitygenerically reduced curves

MSC classification

Primary: 14B05: Singularities
Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 67 , Issue 3 , August 2024 , pp. 990 - 1012
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press on Behalf of The Edinburgh Mathematical Society.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Bondil, R. and D. T., Lê, Caractérisations des éléments superficiels d’un idéal, C. R. Acad. Sci., Paris, Sér. I, Math. 332 (8) (2001), 717–722.CrossRefGoogle Scholar
Brücker, C. and G.-M., Greuel, Deformationen isolierter Kurvensingularitäten mit eingebetteten Komponenten. (Deformations of isolated curve singularities with embedded components), Manuscr. Math. 70 (1) (1990), 93–114.CrossRefGoogle Scholar
Buchweitz, R.-O. and G.-M., Greuel, The Milnor number and deformations of complex curve singularities, Invent. Math. 58 (1980), 241–281.CrossRefGoogle Scholar
Decker, W., Greuel, G.-M., Pfister, G. and Schönemann, H., Singular 4-2-0 – A Computer Algebra System for Polynomial Computations. 2020, http://www.singular.uni-kl.de.Google Scholar
Delgado, F. and H., Maugendre, Special fibres and critical locus for a pencil of plane curve singularities, Compositio Math. 136 (1) (2003), 69–87.CrossRefGoogle Scholar
Delgado, F. and Maugendre, H., Pencils and critical loci on normal surfaces, Rev. Mat. Complut. 34 (3) (2021), 691–714.CrossRefGoogle Scholar
Fernández de Bobadilla, J., Snoussi, J. and Spivakovsky, M., Equisingularity in one-parameter families of generically reduced curves, Int. Math. Res. Not. 2017 (5) (2017), 1589–1609.Google Scholar
Giles Flores, A., Silva, O. N. and Snoussi, J., On tangency in equisingular families of curves and surfaces, Q. J. Math. 71(2) (2020), 485–505.CrossRefGoogle Scholar
Greuel, G.-M., Equisingular and equinormalizable deformations of isolated non-normal singularities, Methods Appl. Anal. 24(2) (2017), 215–276.CrossRefGoogle Scholar
Greuel, G.-M., Lossen, C. and Shustin, E., Introduction to Singularities and Deformations, Springer, Berlin 2007.Google Scholar
Hartshorne, R., Algebraic Geometry. Corr. 3rd Printing, 52. Springer, Cham, 1983.Google Scholar
Laufer, H. B., Normal Two-dimensional Singularities, 71. Princeton University Press Princeton, NJ 1971.Google Scholar
Lê, D. T., and C., Weber, Équisingularité dans les pinceaux de germes de courbes planes et $C^0$-suffisance, Enseign. Math. 43 (3–4) (1997), 355–380.Google Scholar
Matsumura, H., Commutative Ring Theory. Transl. From the Japanese by M. Reid, 8. Cambridge University Press, Cambridge, 1986.Google Scholar
Mumford, D., The topology of normal singularities of an algebraic surface and a criterion for simplicity, Publ. Math., Inst. Hautes Étud. Sci. 9 (1961), 5–22.CrossRefGoogle Scholar
Ngô Viêt, T. and Ikeda, S., When is the Rees algebra Cohen-Macaulay? Commun. Algebra 17 (12) (1989), 2893–2922.Google Scholar
Silva, O. N. and J., Snoussi, Whitney equisingularity in families of generically reduced curves, Manuscr. Math. 163 (3–4) (2020), 463–479.CrossRefGoogle Scholar
Snoussi, J., Limites d’espaces tangents à une surface normale. PhD thesis, Université de Provence France, 1998.CrossRefGoogle Scholar
Snoussi, J., Limites d’espaces tangents à une surface normale, Comment. Math. Helv. 76(1) (2001), 61–88.CrossRefGoogle Scholar