Hostname: page-component-669899f699-8p65j Total loading time: 0 Render date: 2025-04-28T02:43:47.339Z Has data issue: false hasContentIssue false
  • English
  • Français

Derived functors and Hilbert polynomials over regular local rings

Part of: Commutative algebra: Homological methods General commutative ring theory

Published online by Cambridge University Press:  23 October 2024

Tony J. Puthenpurakal Open the ORCID record for Tony J. Puthenpurakal [Opens in a new window]
Tony J. Puthenpurakal*
Affiliation:
Department of Mathematics, IIT Bombay, Powai, Mumbai, India
*
Email: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 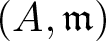$(A,\mathfrak{m})$ be a regular local ring of dimension 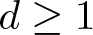$d \geq 1$, I an 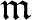$\mathfrak{m}$-primary ideal. Let N be a nonzero finitely generated A-module. Consider the functions

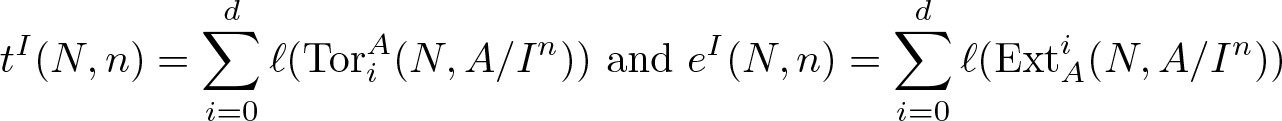\begin{equation*}t^I(N, n) = \sum_{i = 0}^{d}\ell(\text{Tor}^A_i(N, A/I^n)) \ \text{and}\ e^I(N, n) = \sum_{i = 0}^{d}\ell(\text{Ext}_A^i(N, A/I^n))\end{equation*}

of polynomial type and let their degrees be 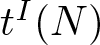$t^I(N) $ and 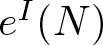$e^I(N)$. We prove that 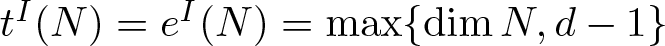$t^I(N) = e^I(N) = \max\{\dim N, d -1 \}$. A crucial ingredient in the proof is that 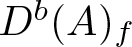$D^b(A)_f$, the bounded derived category of A with finite length cohomology, has no proper thick subcategories.

Keywords

torsion and extension functorsbounded homotopy category of projectives

MSC classification

Primary: 13D02: Syzygies, resolutions, complexes 13D07: Homological functors on modules (Tor, Ext, etc.)
Secondary: 13A30: Associated graded rings of ideals (Rees ring, form ring), analytic spread and related topics 13D40: Hilbert-Samuel and Hilbert-Kunz functions; Poincaré series 13D09: Derived categories
Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 67 , Issue 4 , November 2024 , pp. 1137 - 1147
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press on Behalf of The Edinburgh Mathematical Society.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Crabbe, A., Katz, D., Striuli, J. and Theodorescu, E., Hilbert-Samuel polynomials for the contravariant extension functor, Nagoya Math. J. 198 (2010), 1–22.CrossRefGoogle Scholar
Iyengar, S. and Puthenpurakal, T. J., Hilbert-Samuel functions of modules over Cohen-Macaulay rings, Proc. Amer. Math. Soc. 135(3) (2007), 637–648.CrossRefGoogle Scholar
Kadu, G. and Puthenpurakal, T. J., Bass and Betti numbers of $A/I^n$, J. Algebra 573 (2021), 620–640.CrossRefGoogle Scholar
Katz, D. and Theodorescu, E., On the degree of Hilbert polynomials associated to the torsion functor, Proc. Amer. Math. Soc. 135(10) (2007), 3073–3082.CrossRefGoogle Scholar
Neeman, A., The chromatic tower for $D(R$), With an appendix by Marcel Bökstedt, Topology 31(3) (1992), 519–532.CrossRefGoogle Scholar
Neeman, A., Triangulated categories, Annals of Mathematics Studies, 148, (Princeton University Press, Princeton, NJ, 2001).CrossRefGoogle Scholar
Puthenpurakal, T. J., Hilbert coefficients of a Cohen-Macaulay module, J. Algebra 264(1) (2003), 82–97.CrossRefGoogle Scholar
Sally, J. D., Numbers of Generators of Ideals in Local rings (Marcel Dekker, Inc., New York-Basel, 1978).Google Scholar
Theodorescu, E., Derived functors and Hilbert polynomials, Math. Proc. Cambridge Philos. Soc. 132(1) (2002), 75–88.CrossRefGoogle Scholar