Hostname: page-component-669899f699-ggqkh Total loading time: 0 Render date: 2025-04-28T00:13:24.986Z Has data issue: false hasContentIssue false
  • English
  • Français

Derived functors and Hilbert polynomials over hypersurface rings

Part of: Commutative algebra: Homological methods Local rings and semilocal rings

Published online by Cambridge University Press:  02 April 2025

Tony J. Puthenpurakal Open the ORCID record for Tony J. Puthenpurakal [Opens in a new window]
Tony J. Puthenpurakal*
Affiliation:
Department of Mathematics, IIT Bombay, Powai, Mumbai, Maharashtra, India
*
Email: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 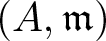$(A,\mathfrak{m} )$ be a hypersurface local ring of dimension 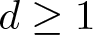$d \geq 1$ and let I be an 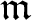$\mathfrak{m} $-primary ideal. We show that there is a integer rI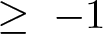$\geq\;-1$ (depending only on I) such that if M is any non-free maximal Cohen–Macaulay (= MCM) A-module the function 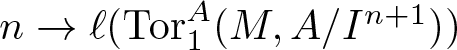$n \rightarrow \ell(\operatorname{Tor}^A_1(M, A/I^{n+1}))$ (which is of polynomial type) has degree rI. Analogous results hold for Hilbert polynomials associated to Ext-functors. Surprisingly, a key ingredient is the classification of thick subcategories of the stable category of MCM A-modules (obtained by Takahashi, see [11, 6.6]).

Keywords

functions of polynomial typederived functorshypersurface ringsstable category of MCM modules13D09

MSC classification

Primary: 13D09: Derived categories
Secondary: 13H10: Special types (Cohen-Macaulay, Gorenstein, Buchsbaum, etc.)
Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , First View , pp. 1 - 11
Check for updates
Copyright
© The Author(s), 2025. Published by Cambridge University Press on Behalf of The Edinburgh Mathematical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Avramov, L. L., Infinite free resolutions. Six Lectures on Commutative Algebra, Progr. Math., Vol. 166, pp. (Birkhäuser, Basel, 1996).Google Scholar
Avramov, L. L. and Buchweitz, R.-O., Support varieties and cohomology over complete intersections, Invent. Math. 142(2) (2000), 285–318.CrossRefGoogle Scholar
Buchweitz, R.-O., Maximal Cohen-Macaulay Modules and Tate Cohomology Over Gorenstein Rings, Mathematical Surveys and Monographs, Vol. 262 (American Mathematical Society, Providence, RI, 2021).Google Scholar
Eisenbud, D., Homological algebra on a complete intersection, with an application to group representations, Trans. Amer. Math. Soc. 260(1) (1980), 35–64.CrossRefGoogle Scholar
Huneke, C. and Wiegand, R., Tensor products of modules, rigidity and local cohomology, Math. Scand. 81(2) (1997), 161–183.CrossRefGoogle Scholar
Katz, D. and Theodorescu, E., On the degree of Hilbert polynomials associated to the torsion functor, Proc. Amer. Math. Soc. 135(10) (2007), 3073–3082.Google Scholar
Neeman, A., Triangulated Categories, Annals of Mathematics Studies, Vol. 148 (Princeton University Press, Princeton, NJ, 2001).Google Scholar
Puthenpurakal, T. J., Hilbert-coefficients of a Cohen-Macaulay module, J. Algebra 264(1) (2003), 82–97.CrossRefGoogle Scholar
Puthenpurakal, T. J., A sub-functor for Ext and Cohen-Macaulay associated graded modules with bounded multiplicity, Trans. Amer. Math. Soc. 373(4) (2020), 2567–2589.Google Scholar
Puthenpurakal, T. J., Derived functors and Hilbert polynomials over regular local rings, Proc. Edinb. Math. Soc. 67(4) (2024), 1137–1147.Google Scholar
Takahashi, R., Classifying thick subcategories of the stable category of Cohen-Macaulay modules, Adv. Math. 225(4) (2010), 2076–2116.Google Scholar
Theodorescu, E., Derived functors and Hilbert polynomials, Math. Proc. Camb. Phil. Soc. 132(1) (2002), 75–88.CrossRefGoogle Scholar