Hostname: page-component-669899f699-vbsjw Total loading time: 0 Render date: 2025-04-28T08:35:25.920Z Has data issue: false hasContentIssue false
  • English
  • Français

Defect relation for holomorphic maps from complex discs into projective varieties and hypersurfaces

Part of: Holomorphic functions of several complex variables Entire and meromorphic functions, and related topics Holomorphic mappings and correspondences

Published online by Cambridge University Press:  22 November 2024

Si Duc Quang Open the ORCID record for Si Duc Quang [Opens in a new window]
Si Duc Quang*
Affiliation:
Department of Mathematics, Hanoi National University of Education, 136-Xuan Thuy, Cau Giay, Hanoi, Vietnam
*
Email: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper, we establish a second main theorem for holomorphic maps with finite growth index on complex discs intersecting arbitrary families of hypersurfaces (fixed and moving) in projective varieties, which gives an above bound of the sum of truncated defects. Our result also generalizes and improves many previous second main theorems for holomorphic maps from 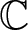${\mathbb{C}}$ intersecting hypersurfaces (moving and fixed) in projective varieties.

Keywords

second main theoremholomorphic maphypersurfacefinite growth index

MSC classification

Primary: 32H30: Value distribution theory in higher dimensions
Secondary: 30D35: Distribution of values, Nevanlinna theory 32A22: Nevanlinna theory (local); growth estimates; other inequalities
Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 68 , Issue 1 , February 2025 , pp. 157 - 172
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press on Behalf of The Edinburgh Mathematical Society.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Dethloff, G. and Tan, T. V., Holomorphic curves into algebraic varities intersecting moving hypersurfaces targets, Acta Math. Vietnamica, 45(1) (2020), 291–308.CrossRefGoogle Scholar
Evertse, J. and Ferretti, R., Diophantine inequalities on projective varieties, Int. Math. Res. Not., 2002(25) (2002), 1295–1330.CrossRefGoogle Scholar
Giang, L., An explicit estimate on multiplicity truncation in the degenerated second main theorem, Houston J. Math., 42(2) (2016), 447–462.Google Scholar
Quang, S. D., Generalizations of degeneracy second main theorem and Schmidt’s subspace theorem, Pacific J. Math., 318(1) (2022), 153–188.CrossRefGoogle Scholar
Quang, S. D., An effective function field version of Schmidt’s subspace theorem for projective varieties, with arbitrary families of homogenous polynomials, J. Number Theory, 241 (2022), 563–580.CrossRefGoogle Scholar
Quang, S. D., Meromorphic mappings into projective varieties with arbitrary families of moving hypersurfaces, J. Geom. Anal., 32 (2022), .Google Scholar
Ru, M., Holomorphic curves into algebraic varieties, Ann. Math., 169(1) (2009), 255–267.CrossRefGoogle Scholar
Ru, M. and Sibony, N., The second main theorem in the hyperbolic case, Math. Ann., 377(1–2) (2020), 759–795.CrossRefGoogle Scholar
Shi, L., Degenerated second main theorem for holomorphic curves into algebraic varieties, Int. J. Math. 31(06) (2020), .CrossRefGoogle Scholar
Thai, D. D. and Quang, S. D., Cartan-Nochka theorem with truncated counting functions for moving targets, Acta Math. Vietnamica, 35(1) (2010), 173–197.Google Scholar