Hostname: page-component-669899f699-vbsjw Total loading time: 0 Render date: 2025-04-25T23:14:50.724Z Has data issue: false hasContentIssue false
  • English
  • Français

Bounds on the Pythagoras number and indecomposables in biquadratic fields

Part of: Forms and linear algebraic groups Algebraic number theory: global fields

Published online by Cambridge University Press:  31 March 2025

Magdaléna Tinková Open the ORCID record for Magdaléna Tinková [Opens in a new window]
Magdaléna Tinková*
Affiliation:
Department of Algebra, Faculty of Mathematics and Physics, Charles University, Sokolovská 83, Praha 8, Czech Republic Faculty of Information Technology, Czech Technical University in Prague, Thákurova 9, Praha 6, Czech Republic TU Graz, Institute of Analysis and Number Theory, Kopernikusgasse 24/II, Graz, Austria
*
Email: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

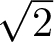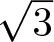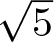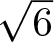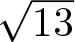We show that for all real biquadratic fields not containing $\sqrt{2}$, $\sqrt{3}$, $\sqrt{5}$, $\sqrt{6}$, $\sqrt{7}$ and $\sqrt{13}$, the Pythagoras number of the ring of algebraic integers is at least 6. We also provide an upper bound on the norm and the minimal (codifferent) trace of additively indecomposable integers in some families of these fields.

Keywords

Pythagoras numberbiquadratic fieldsadditively indecomposable integers

MSC classification

Primary: 11E25: Sums of squares and representations by other particular quadratic forms
Secondary: 11R16: Cubic and quartic extensions 11R80: Totally real fields
Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , First View , pp. 1 - 26
Check for updates
Copyright
© The Author(s), 2025. Published by Cambridge University Press on Behalf of The Edinburgh Mathematical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Blomer, V., and Kala, V., Number fields without n-ary universal quadratic forms, Math. Proc. Camb. Phil. Soc. 159(2) (2015), 239–252.CrossRefGoogle Scholar
Brunotte, H., Zur Zerlegung totalpositiver Zahlen in Ordnungen totalreeller algebraischer Zahlkörper, Arch. Math. 41 (1983), 502–503.CrossRefGoogle Scholar
Čech, M., Lachman, D., Svoboda, J., Tinková, M., and Zemková, K., Universal quadratic forms and indecomposables over biquadratic fields, Math. Nachr. 292(3) (2019), 540–555.CrossRefGoogle Scholar
Dress, A., and Scharlau, R., Indecomposable totally positive numbers in real quadratic orders, J. Number Theory 14(3) (1982), 292–306.CrossRefGoogle Scholar
Gil Muñoz, D., and Tinková, M., Additive structure of non-monogenic simplest cubic fields, Ramanujan J. 66(3) (2025), 47.CrossRefGoogle Scholar
He, Z. and Hu, Y., Pythagoras number of quartic orders containing $\sqrt{2}$. https://arxiv.org/abs/2204.10468.Google Scholar
Jang, S. W. and Kim, B. M., A refinement of the Dress-Scharlau theorem, J. Number Theory 158 (2016), 234–243.CrossRefGoogle Scholar
Jarvis, F., Algebraic Number Theory (Springer, 2007).Google Scholar
Kala, V., Universal quadratic forms and elements of small norm in real quadratic fields, Bull. Aust. Math. Soc. 94(1) (2016), 7–14.CrossRefGoogle Scholar
Kala, V., Norms of indecomposable integers in real quadratic fields, J. Number Theory 166 (2016), 193–207.CrossRefGoogle Scholar
Kala, V., Number fields without universal quadratic forms of small rank exist in most degrees, Math. Proc. Camb. Phil. Soc. 174(2) (2023), 225–231.CrossRefGoogle Scholar
Kala, V., Universal quadratic forms and indecomposables in number fields: A survey, Commun. Math. 31(2) (2023), 81–114.Google Scholar
Kala, V., and Man, S. H., Sails for universal quadratic forms, Sel. Math. 31(2) (2025), 26.CrossRefGoogle Scholar
Kala, V., Sgallová, E. and Tinková, M., Arithmetic of cubic number fields: Jacobi–Perron, Pythagoras, and indecomposables, J. Number Theory 273 (2025), 37–95.CrossRefGoogle Scholar
Kala, V., and Svoboda, J., Universal quadratic forms over multiquadratic fields, Ramanujan J. 48(1) (2019), 151–157.CrossRefGoogle Scholar
Kala, V., and Tinková, M., Universal quadratic forms, small norms and traces in families of number fields, Int. Math. Res. Not. 2023(9) (2023), 7541–7577.CrossRefGoogle Scholar
Kala, V. and Yatsyna, P., Lifting problem for universal quadratic forms, Adv. Math. 377 (2021), 107497.CrossRefGoogle Scholar
Kala, V., and Yatsyna, P., On Kitaoka’s conjecture and lifting problem for universal quadratic forms, Bull. London Math. Soc. 55(2) (2023), 854–864.CrossRefGoogle Scholar
Kim, D., and Lee, S. H., Lifting problem for universal quadratic forms over totally real cubic number fields, Bull. London Math. Soc. 56(3) (2024), 1192–1206.CrossRefGoogle Scholar
Krásenský, J., A cubic ring of integers with the smallest Pythagoras number, Arch. Math. 118(1) (2022), 39–48.CrossRefGoogle Scholar
Krásenský, J., Raška, M., and Sgallová, E., Pythagoras numbers of orders in biquadratic fields, Expo. Math. 40(4) (2022), 1181–1228.CrossRefGoogle Scholar
Krásenský, J., Tinková, M., and Zemková, K., There are no universal ternary quadratic forms over biquadratic fields, Proc. Edinb. Math. Soc. 63(3) (2020), 861–912.CrossRefGoogle Scholar
Man, S. H., Minimal rank of universal lattices and number of indecomposable elements in real multiquadratic fields, Adv. Math. 447 (2024), 109694.CrossRefGoogle Scholar
Narkiewicz, W., Elementary and Analytic Theory of Algebraic Numbers, 3rd edition (Springer-Verlag, Berlin, 2004).CrossRefGoogle Scholar
Perron, O., Die Lehre von den Kettenbrüchen (B. G. Teubner, 1913).Google Scholar
Peters, M., Quadratische Formen über Zahlringen, Acta Arith. 24 (1973), 157–164.CrossRefGoogle Scholar
Scharlau, R., On the Pythagoras number of orders in totally real number fields, J. Reine Angew. Math. 316 (1980), 208–210.Google Scholar
Tinková, M., Trace and norm of indecomposable integers in cubic orders, Ramanujan J. 61(4) (2023), 1121–1144.CrossRefGoogle Scholar
Tinková, M., On the Pythagoras number of the simplest cubic fields, Acta Arith. 208(4) (2023), 325–354.CrossRefGoogle Scholar
Tinková, M. and Voutier, P., Indecomposable integers in real quadratic fields, J. Number Theory 212 (2020), 458–482.CrossRefGoogle Scholar
Williams, K. S., Integers of biquadratic fields, Can. Math. Bull. 13(4) (1970), 519–526.CrossRefGoogle Scholar
Yatsyna, P., A lower bound for the rank of a universal quadratic form with integer coefficients in a totally real field, Comment. Math. Helvet. 94(2) (2019), 221–239.CrossRefGoogle Scholar