Hostname: page-component-669899f699-swprf Total loading time: 0 Render date: 2025-04-30T07:01:52.541Z Has data issue: false hasContentIssue false
  • English
  • Français

A REMARK ON THE N-INVARIANT GEOMETRY OF BOUNDED HOMOGENEOUS DOMAINS

Part of: Complex spaces with a group of automorphisms Genetics and population dynamics Pseudoconvex domains Analytic continuation Automorphic functions

Published online by Cambridge University Press:  23 May 2024

LAURA GEATTI Open the ORCID record for LAURA GEATTI [Opens in a new window]  and
ANDREA IANNUZZI Open the ORCID record for ANDREA IANNUZZI [Opens in a new window]
LAURA GEATTI*
Affiliation:
Dipartimento di Matematica Università di Roma Tor Vergata Via della Ricerca Scientifica 1 I-00133 Roma Italy
ANDREA IANNUZZI
Affiliation:
Dipartimento di Matematica Università di Roma Tor Vergata Via della Ricerca Scientifica 1 I-00133 Roma Italy [email protected]
*
[email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 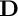$\mathbf {D}$ be a bounded homogeneous domain in 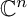${\mathbb {C}}^n$. In this note, we give a characterization of the Stein domains in 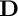$\mathbf {D}$ which are invariant under a maximal unipotent subgroup N of 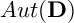$Aut(\mathbf {D})$. We also exhibit an N-invariant potential of the Bergman metric of 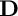$\mathbf {D}$, expressed in a Lie theoretical fashion. These results extend the ones previously obtained by the authors in the symmetric case.

Keywords

bounded homogeneous domainsunipotent groupStein subdomainsmoment map

MSC classification

Primary: 32M10: Homogeneous complex manifolds 32T05: Domains of holomorphy 32D10: Envelopes of holomorphy
Type
Article
Information
Nagoya Mathematical Journal , Volume 256 , December 2024 , pp. 928 - 937
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press on behalf of Foundation Nagoya Mathematical Journal

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

D’Atri, J. E., Holomorphic sectional curvatures of bounded domains and related questions , Trans. Amer. Math. Soc. 256 (1979), 405–413.CrossRefGoogle Scholar
Dorfmeister, J., Simply transitive groups and Kähler structures on homogeneous Siegel domains , Trans. Amer. Math. Soc. 288 (1985), 293–305.Google Scholar
Geatti, L. and Iannuzzi, A., Geometry of Hermitian symmetric spaces under the action of a maximal unipotent group , Int. J. Math. 35 (2024), 2350102, DOI 10.1142/S0129167X23501021 CrossRefGoogle Scholar
Gindikin, S., Pyatetskii-Shapiro, I. I. and Vinberg, E., “Kähler manifolds” in Geometry of bounded domains (C.I.M.E.), Edizioni Cremonese, Roma, 1968, pp. 3–87.Google Scholar
Gunning, R. C., Introduction to holomorphic functions of several variables, Function Theory (Wadsworth & Brooks/Cole Mathematics Series), Vol. 1, Wadsworth & Brooks/Cole, Pacific Grove, CA, 1990.Google Scholar
Hilgert, J., Neeb, K.-H. and Plank, W., Symplectic convexity theorems and coadjoint orbits , Comp. Math. (2) 94 (1994), 129–180.Google Scholar
Koszul, J. L., Sur la forme Hermitienne canonique des espaces homogènes complexes , Canad. J. Math. 7 (1955), 562–576.CrossRefGoogle Scholar
Pyatetskii-Shapiro, I. I., Automorphic functions and the geometry of classical domains, Gordon and Breach, New York, 1969.Google Scholar
Rossi, H., On envelopes of holomorphy , Comm. Pure Appl. Math. 16 (1963), 9–17.CrossRefGoogle Scholar
Rossi, H. and Vergne, M., Representations of certain solvable Lie groups on Hilbert spaces of holomorphic functions and the application to the holomorphic discrete series of a semisimple Lie group , J. Funct. Anal. 13 (1973), 324–389.CrossRefGoogle Scholar