Hostname: page-component-669899f699-rg895 Total loading time: 0 Render date: 2025-04-30T06:18:51.044Z Has data issue: false hasContentIssue false
  • English
  • Français

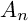BIRATIONAL GEOMETRY OF SEXTIC DOUBLE SOLIDS WITH A COMPOUND $A_n$ SINGULARITY

Part of: Birational geometry Surfaces and higher-dimensional varieties

Published online by Cambridge University Press:  18 September 2024

ERIK PAEMURRU Open the ORCID record for ERIK PAEMURRU [Opens in a new window]
ERIK PAEMURRU*
Affiliation:
Mathematik und Informatik Universität des Saarlandes Saarbrücken 66123 Germany
*
[email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Sextic double solids, double covers of 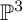$\mathbb P^3$ branched along a sextic surface, are the lowest degree Gorenstein terminal Fano 3-folds, hence are expected to behave very rigidly in terms of birational geometry. Smooth sextic double solids, and those which are 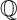$\mathbb Q$-factorial with ordinary double points, are known to be birationally rigid. In this paper, we study sextic double solids with an isolated compound 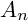$A_n$ singularity. We prove a sharp bound 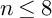$n \leq 8$, describe models for each n explicitly, and prove that sextic double solids with 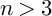$n> 3$ are birationally nonrigid.

Keywords

Fano 3-foldsSarkisov programbirational rigidity

MSC classification

Primary: 14J45: Fano varieties
Secondary: 14J30: $3$-folds 14J17: Singularities 14E30: Minimal model program (Mori theory, extremal rays) 14E05: Rational and birational maps
Type
Article
Information
Nagoya Mathematical Journal , Volume 256 , December 2024 , pp. 970 - 1021
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press on behalf of Foundation Nagoya Mathematical Journal

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

Footnotes

The author was supported by the Engineering and Physical Sciences Research Council (Grant No. 1820497) while in Loughborough University and the London Mathematical Society Early Career Fellowship (Grant No. ECF-1920-24) while in Imperial College London.

References

Ahmadinezhad, H., On pliability of del Pezzo fibrations and Cox rings , J. Reine Angew. Math. 723 (2017), 101–125.CrossRefGoogle Scholar
Ahmadinezhad, H. and Kaloghiros, A.-S., Non-rigid quartic 3-folds , Compos. Math. 152 (2016), no. 5, 955–983.CrossRefGoogle Scholar
Ahmadinezhad, H. and Okada, T., Birationally rigid Pfaffian Fano 3-folds , Algebr. Geom. 5 (2018), no. 2, 160–199.CrossRefGoogle Scholar
Ahmadinezhad, H. and Zucconi, F., Mori dream spaces and birational rigidity of Fano 3-folds , Adv. Math. 292 (2016), 410–445.CrossRefGoogle Scholar
Barth, W., Two projective surfaces with many nodes, admitting the symmetries of the icosahedron , J. Algebraic Geom. 5 (1996), no. 1, 173–186.Google Scholar
Basset, A. B., The maximum number of double points on a surface , Nature. 73 (1906), no. 1889, 246.CrossRefGoogle Scholar
Birkar, C., Cascini, P., Hacon, C. D. and McKernan, J., Existence of minimal models for varieties of log general type , J. Amer. Math. Soc. 23 (2010), no. 2, 405–468.CrossRefGoogle Scholar
Brown, G., Flips arising as quotients of hypersurfaces . Math. Proc. Camb. Philos. Soc. 127 (1999), no. 1, 13–31.CrossRefGoogle Scholar
Brown, G. and Buczyński, J., Maps of toric varieties in Cox coordinates . Fundam. Math. 222 (2013), no. 3, 213–267.CrossRefGoogle Scholar
Brown, G. and Zucconi, F., Graded rings of rank 2 Sarkisov links , Nagoya Math. J. 197 (2010), 1–44.CrossRefGoogle Scholar
Campana, F., Dethloff, G., Grauert, H., Petemell, Th. and Remmert, R., Several complex variables VII: Sheaf-theoretical methods in complex analysis, Encyclopaedia of Mathematical Sciences, Vol. 74, Springer, Berlin, 1994. A reprint of Current problems in mathematics. Fundamental directions (in Russian), Vol. 74, Vseross. Inst. Nauchn. i Tekhn. Inform. (VINITI), Moscow.Google Scholar
Catanese, F. and Ceresa, G., Constructing sextic surfaces with a given number $d$ of nodes , J. Pure Appl. Algebra. 23 (1982), no. 1, 1–12.CrossRefGoogle Scholar
Cheltsov, I. and Grinenko, M., Birational rigidity is not an open property , Bull. Korean Math. Soc. 54 (2017), no. 5, 1485–1526.Google Scholar
Cheltsov, I. and Park, J., “Sextic double solids” in Bogomolov, F. and Tschinkel, Y. (eds.), Cohomological and geometric approaches to rationality problems: New perspectives, Birkhäuser, Boston, 2010, pp. 75–132.CrossRefGoogle Scholar
Cheltsov, I. and Park, J., Birationally rigid Fano threefold hypersurfaces, Memoirs of the American Mathematical Society, Vol. 246(1167), American Mathematical Society, Providence, RI, 2017, v + 117.Google Scholar
Cheltsov, I. and Shramov, C., Finite collineation groups and birational rigidity , Sel. Math. New Ser. 25 (2019), no. 5, Article No. 71.CrossRefGoogle Scholar
Corti, A., Factoring birational maps of threefolds after Sarkisov , J. Algebraic Geom. 4 (1995), no. 2, 223–254.Google Scholar
Corti, A. and Mella, M., Birational geometry of terminal quartic 3-folds. I , Amer. J. Math. 126 (2004), no. 4, 739–761.CrossRefGoogle Scholar
Corti, A., Pukhlikov, A. and Reid, M., “Fano 3-fold hypersurfaces” in Explicit birational geometry of 3-folds, London Mathematical Society Lecture Note Series, Vol. 281, Cambridge University Press, Cambridge, 2000, pp. 175–258.CrossRefGoogle Scholar
Cox, D. A., The homogeneous coordinate ring of a toric variety , J. Algebraic Geom. 4 (1995), no. 1, 17–50.Google Scholar
Cox, D. A., Little, J. B. and Schenck, H. K., Toric varieties, Graduate Studies in Mathematics, Vol. 124, American Mathematical Society, Providence, RI, 2011.CrossRefGoogle Scholar
de Fernex, T., Birational rigidity of singular Fano hypersurfaces , Ann. Sc. Norm. Super. Pisa Cl. Sci. (5). 17 (2017), no. 3, 911–929.Google Scholar
Eckl, T. and Pukhlikov, A., Effective birational rigidity of Fano double hypersurfaces , Arnold Math. J. 4 (2018), nos. 3–4, 505–521.CrossRefGoogle Scholar
Eisenbud, D., Commutative algebra: With a view toward algebraic geometry, Graduate Texts in Mathematics, Springer, New York, 1995.CrossRefGoogle Scholar
Greuel, G.-M., Lossen, C. and Shustin, E., Introduction to singularities and deformations, Springer Monographs in Mathematics, Springer, Berlin, 2007.Google Scholar
Hacon, C. D. and McKernan, J., The Sarkisov program , J. Algebraic Geom. 22 (2013), no. 2, 389–405.CrossRefGoogle Scholar
Hu, Y. and Keel, S., Mori dream spaces and GIT , Michigan Math. J. 48 (2000), no. 1, 331–348.CrossRefGoogle Scholar
Iskovskih, V. A. and Manin, J. I., Three-dimensional quartics and counterexamples to the Lüroth problem , Mat. Sb. (N.S.). 86 (1971), no. 128, 140–166.Google Scholar
Iskovskikh, V. A., Birational automorphisms of three-dimensional algebraic varieties , J. Sov. Math. 13 (1980), no. 6, 815–868.CrossRefGoogle Scholar
Iskovskikh, V. A. and Prokhorov, Y. G., Algebraic geometry V: Fano varieties, Springer, Berlin–Heidelberg, 1999.Google Scholar
Jaffe, D. B. and Ruberman, D., A sextic surface cannot have $66$ nodes , J. Algebraic Geom. 6 (1997), no. 1, 151–168.Google Scholar
Kawakita, M., General elephants of three-fold divisorial contractions , J. Amer. Math. Soc. 16 (2003), no. 2, 331–362.CrossRefGoogle Scholar
Kawamata, Y., Crepant blowing-up of $3$ -dimensional canonical singularities and its application to degenerations of surfaces , Ann. Math. 127 (1988), no. 1, 93–163.CrossRefGoogle Scholar
Kawamata, Y., “Divisorial contractions to 3-dimensional terminal quotient singularities” in Higher-dimensional complex varieties (Trento, 1994), de Gruyter, Berlin, 1996, pp. 241–246.Google Scholar
Kollár, J., Real algebraic threefolds. I. Terminal singularities , Collect. Math. 49 (1998), nos. (2–3, 335–360. Dedicated to the memory of Fernando Serrano.Google Scholar
Kollár, J. and Mori, S., Classification of three-dimensional flips , J. Amer. Math. Soc. 5 (1992), no. 3, 533–703.CrossRefGoogle Scholar
Kollár, J. and Mori, S., Birational geometry of algebraic varieties, Tracts in Mathematics, Vol. 134, Cambridge University Press, Cambridge, 1998. With the collaboration of C. H. Clemens and A. Corti, Translated from the 1998 Japanese original.CrossRefGoogle Scholar
Krylov, I., Birational geometry of del Pezzo fibrations with terminal quotient singularities , J. Lond. Math. Soc. (2). 97 (2018), no. 2, 222–246.CrossRefGoogle Scholar
Liu, Q., Algebraic geometry and arithmetic curves, Translated by Reinie Erné, Oxford Graduate Texts in Mathematics, Vol. 6, Oxford University Press, Oxford, 2006.Google Scholar
Mather, J. N. and Yau, S. S. T., Classification of isolated hypersurface singularities by their moduli algebras , Invent. Math. 69 (1982), no. 2, 243–251.CrossRefGoogle Scholar
Mavlyutov, A. R., Cohomology of complete intersections in toric varieties , Pacific J. Math. 191 (1999), no. 1, 133–144.CrossRefGoogle Scholar
Namikawa, Y., Smoothing Fano $3$ -folds , J. Algebraic Geom. 6 (1997), no. 2, 307–324.Google Scholar
Okada, T., Birational Mori fiber structures of $\mathbb{Q}$ -Fano 3-fold weighted complete intersections , Proc. Lond. Math. Soc. (3). 109 (2014), no. 6, 1549–1600.CrossRefGoogle Scholar
Papadakis, S. A. and Reid, M., Kustin–Miller unprojection without complexes , J. Algebraic Geom. 13 (2004), no. 3, 563–577.CrossRefGoogle Scholar
Prokhorov, Y. G., The rationality problem for conic bundles , Uspekhi Mat. Nauk. 73 (2018), no. 3(441), 3–88.CrossRefGoogle Scholar
Pukhlikov, A. V., Birational automorphisms of double spaces with singularities , J. Math. Sci. (New York). 85 (1997), no. 4, 2128–2141.CrossRefGoogle Scholar
Reid, M., “Canonical 3-folds” in Journées de géometrie algébrique d’Angers, Juillet 1979/algebraic geometry, Angers, 1979, Sijthoff & Noordhoff, Alphen aan den Rijn, Germantown, MD, 1980, pp. 273–310.Google Scholar
Reid, M., “Minimal models of canonical 3-folds” in Algebraic varieties and analytic varieties (Tokyo, 1981), Advanced Studies in Pure Mathematics, Vol. 1, North-Holland, Amsterdam, 1983, pp. 131–180.CrossRefGoogle Scholar
Reid, M., “Graded rings and birational geometry” in K. Ohno (ed.), Proceedings of algebraic geometry symposium (Kinosaki, October 2000), pp. 1–72. https://repository.kulib.kyoto-u.ac.jp/dspace/handle/2433/214728.Google Scholar
Thom, R., Stabilité structurelle et morphogénèse: Essai d’une théorie générale des modèles, Mathematical Physics Monograph Series, W. A. Benjamin, Inc., Reading, MA, 1972.Google Scholar
Wahl, J., Nodes on sextic hypersurfaces in ${\mathbb{P}}^3$ , J. Differ. Geom. 48 (1998), no. 3, 439–444.CrossRefGoogle Scholar
Yamamoto, Y., Divisorial contractions to $cDV$ points with discrepancy greater than 1 , Kyoto J. Math. 58 (2018), no. 3, 529–567.CrossRefGoogle Scholar
Zhang, Q., Rational connectedness of log $\mathbb{Q}$ -Fano varieties , J. Reine Angew. Math. 590 (2006), 131–142.Google Scholar