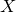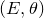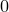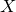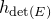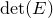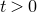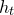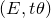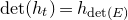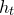1. Introduction
1.1 Background
Let
![]() $X$
be a Riemann surface. Let
$X$
be a Riemann surface. Let
![]() $(E,\overline{\partial }_E,\theta )$
be a Higgs bundle of rank
$(E,\overline{\partial }_E,\theta )$
be a Higgs bundle of rank
![]() $r$
on
$r$
on
![]() $X$
. Let
$X$
. Let
![]() $h$
be a Hermitian metric of
$h$
be a Hermitian metric of
![]() $E$
. We obtain the Chern connection
$E$
. We obtain the Chern connection
![]() $\nabla _h$
of
$\nabla _h$
of
![]() $(E,\overline{\partial }_E,h)$
and the adjoint
$(E,\overline{\partial }_E,h)$
and the adjoint
![]() $\theta ^{\dagger }_h$
of
$\theta ^{\dagger }_h$
of
![]() $\theta$
with respect to
$\theta$
with respect to
![]() $h$
. Let
$h$
. Let
![]() $R(h)$
denote the curvature of
$R(h)$
denote the curvature of
![]() $\nabla _h$
. The metric
$\nabla _h$
. The metric
![]() $h$
is called a harmonic metric of
$h$
is called a harmonic metric of
![]() $(E,\overline{\partial }_E,\theta )$
if
$(E,\overline{\partial }_E,\theta )$
if
The metric
![]() $h$
is called a decoupled harmonic metric of
$h$
is called a decoupled harmonic metric of
![]() $(E,\overline{\partial }_E,\theta )$
if
$(E,\overline{\partial }_E,\theta )$
if
Suppose that
![]() $X$
is compact and that
$X$
is compact and that
![]() $(E,\overline{\partial }_E,\theta )$
is stable of degree
$(E,\overline{\partial }_E,\theta )$
is stable of degree
![]() $0$
. Let
$0$
. Let
![]() $\Sigma _{E,\theta }$
denote the spectral curve of
$\Sigma _{E,\theta }$
denote the spectral curve of
![]() $(E,\theta )$
. We assume that
$(E,\theta )$
. We assume that
![]() $(E,\overline{\partial }_E,\theta )$
is generically regular semisimple, i.e.
$(E,\overline{\partial }_E,\theta )$
is generically regular semisimple, i.e.
![]() $D(E,\theta )=\bigl \{ P\in X\,\big |\,|T^{\ast }_PX\cap \Sigma _{E,\theta }|\lt r \bigr \}$
is a finite subset of
$D(E,\theta )=\bigl \{ P\in X\,\big |\,|T^{\ast }_PX\cap \Sigma _{E,\theta }|\lt r \bigr \}$
is a finite subset of
![]() $X$
.
$X$
.
Let
![]() $h_{\det (E)}$
be a flat metric of
$h_{\det (E)}$
be a flat metric of
![]() $\det (E)$
. According to Hitchin [Reference HitchinHit87] and Simpson [Reference SimpsonSim88],
$\det (E)$
. According to Hitchin [Reference HitchinHit87] and Simpson [Reference SimpsonSim88],
![]() $(E,\overline{\partial }_E,\theta )$
has a unique harmonic metric
$(E,\overline{\partial }_E,\theta )$
has a unique harmonic metric
![]() $h$
such that
$h$
such that
![]() $\det (h)=h_{\det (E)}$
. Because
$\det (h)=h_{\det (E)}$
. Because
![]() $(E,\overline{\partial }_E,t\theta )$
is stable of degree
$(E,\overline{\partial }_E,t\theta )$
is stable of degree
![]() $0$
for any
$0$
for any
![]() $t\gt 0$
, there exists a unique harmonic metric
$t\gt 0$
, there exists a unique harmonic metric
![]() $h_t$
of
$h_t$
of
![]() $(E,\overline{\partial }_E,t\theta )$
for any
$(E,\overline{\partial }_E,t\theta )$
for any
![]() $t\gt 0$
such that
$t\gt 0$
such that
![]() $\det (h_t)=h_{\det (E)}$
. We are interested in the behaviour of
$\det (h_t)=h_{\det (E)}$
. We are interested in the behaviour of
![]() $h_t$
as
$h_t$
as
![]() $t\to \infty$
. See [Reference Gaiotto, Moore and NeitzkeGMN10], [Reference Katzarkov, Noll, Pandit and SimpsonKNP15] and [Reference Mazzeo, Swoboda, Weiss and WittMSW16] for the motivation for this study. It is related to the geometric P=W conjecture [Reference SzabóSza21, Reference SzabóSza22]. See also helpful survey papers [Reference LiLi19, Reference SwobodaSwo21].
$t\to \infty$
. See [Reference Gaiotto, Moore and NeitzkeGMN10], [Reference Katzarkov, Noll, Pandit and SimpsonKNP15] and [Reference Mazzeo, Swoboda, Weiss and WittMSW16] for the motivation for this study. It is related to the geometric P=W conjecture [Reference SzabóSza21, Reference SzabóSza22]. See also helpful survey papers [Reference LiLi19, Reference SwobodaSwo21].
For any simply connected relatively compact open subset
![]() $K$
of
$K$
of
![]() $X\setminus D(E,\theta )$
, there exists a decomposition of the Higgs bundle
$X\setminus D(E,\theta )$
, there exists a decomposition of the Higgs bundle
 \begin{align} (E,\overline{\partial }_E,\theta )_{|K} =\bigoplus _{i=1}^{r} (E_{K,i},\overline{\partial }_{E_{K,i}},\theta _{K,i}) \end{align}
\begin{align} (E,\overline{\partial }_E,\theta )_{|K} =\bigoplus _{i=1}^{r} (E_{K,i},\overline{\partial }_{E_{K,i}},\theta _{K,i}) \end{align}
such that
![]() $\mathop{\textrm{rank}}\nolimits E_{K,i}=1$
. According to [Reference MochizukiMoc16], there exist
$\mathop{\textrm{rank}}\nolimits E_{K,i}=1$
. According to [Reference MochizukiMoc16], there exist
![]() $C(K)\gt 0,\epsilon (K)\gt 0$
such that
$C(K)\gt 0,\epsilon (K)\gt 0$
such that
for any local sections
![]() $u$
and
$u$
and
![]() $v$
of
$v$
of
![]() $E_{K,i}$
and
$E_{K,i}$
and
![]() $E_{K,j}$
$E_{K,j}$
![]() $(i\neq j)$
in the decomposition (1). This implies that there exist
$(i\neq j)$
in the decomposition (1). This implies that there exist
![]() $C'(K)\gt 0$
and
$C'(K)\gt 0$
and
![]() $\epsilon '(K)\gt 0$
such that
$\epsilon '(K)\gt 0$
such that
As a result, for any sequence
![]() $t(i)\to \infty$
, there exist a subsequence
$t(i)\to \infty$
, there exist a subsequence
![]() $t'(j)\to \infty$
and gauge transformations
$t'(j)\to \infty$
and gauge transformations
![]() $g_{t'(j)}$
such that the sequence
$g_{t'(j)}$
such that the sequence
![]() $g_{t'(j)}^{\ast }h_{t'(j)}$
is convergent to a decoupled harmonic metric of
$g_{t'(j)}^{\ast }h_{t'(j)}$
is convergent to a decoupled harmonic metric of
![]() $(E,\overline{\partial }_E,\theta )_{|X\setminus D(E,\theta )}$
in the
$(E,\overline{\partial }_E,\theta )_{|X\setminus D(E,\theta )}$
in the
![]() $C^{\infty }$
-sense locally on
$C^{\infty }$
-sense locally on
![]() $X\setminus D(E,\theta )$
.
$X\setminus D(E,\theta )$
.
We may ask the following questions under appropriate assumptions.
-
Q1 Is there a sequence of gauge transformations
 $g_t$
such that
$g_t$
such that
 $g_t^{\ast }h_t$
is convergent as
$g_t^{\ast }h_t$
is convergent as
 $t\to \infty$
locally on
$t\to \infty$
locally on
 $X\setminus D(E,\theta )$
. In other words, is the limit independent of the choice of a subsequence?
$X\setminus D(E,\theta )$
. In other words, is the limit independent of the choice of a subsequence? -
Q2 Let
 $K\subset X\setminus D(E,\theta )$
be any relatively compact open subset. Then, is the order of the convergence on
$K\subset X\setminus D(E,\theta )$
be any relatively compact open subset. Then, is the order of the convergence on
 $K$
dominated by
$K$
dominated by
 $e^{-\delta (K) t}$
for some
$e^{-\delta (K) t}$
for some
 $\delta (K)\gt 0$
?
$\delta (K)\gt 0$
?
In the rank two case, under the assumption that
![]() $\Sigma _{E,\theta }$
is smooth, Mazzeo et al. [Reference Mazzeo, Swoboda, Weiss and WittMSW16] solved the both questions completely. In [Reference MochizukiMoc16], the question Q1 was solved without assuming the smoothness of the spectral curve. In the higher rank case, Collier and Li [Reference Collier and LiCL17] solved both questions for cyclic Higgs bundles. Fredrickson [Reference FredricksonFred] studied both questions when the spectral curve is smooth, under a mild assumption on the ramification of the spectral curve over
$\Sigma _{E,\theta }$
is smooth, Mazzeo et al. [Reference Mazzeo, Swoboda, Weiss and WittMSW16] solved the both questions completely. In [Reference MochizukiMoc16], the question Q1 was solved without assuming the smoothness of the spectral curve. In the higher rank case, Collier and Li [Reference Collier and LiCL17] solved both questions for cyclic Higgs bundles. Fredrickson [Reference FredricksonFred] studied both questions when the spectral curve is smooth, under a mild assumption on the ramification of the spectral curve over
![]() $X$
(see Remark 1.2 and [Reference FredricksonFred, Proposition 2.2, (2.9)]).
$X$
(see Remark 1.2 and [Reference FredricksonFred, Proposition 2.2, (2.9)]).
Remark 1.1. Chronologically, the study [Reference MochizukiMoc16] was inspired by the previous research in [Reference Collier and LiCL17], [Reference Katzarkov, Noll, Pandit and SimpsonKNP15] and [Reference Mazzeo, Swoboda, Weiss and WittMSW16].
Remark 1.2. Let
![]() $Q\in \Sigma _{E,\theta }$
be a critical point of
$Q\in \Sigma _{E,\theta }$
be a critical point of
![]() $\pi :\Sigma _{E,\theta }\to X$
. Put
$\pi :\Sigma _{E,\theta }\to X$
. Put
![]() $P=\pi (Q)$
. Let
$P=\pi (Q)$
. Let
![]() $(X_P,z)$
be a coordinate neighbourhood around
$(X_P,z)$
be a coordinate neighbourhood around
![]() $P$
. By using the holomorphic
$P$
. By using the holomorphic
![]() $1$
-form
$1$
-form
![]() $dz$
, we obtain the trivialization
$dz$
, we obtain the trivialization
![]() $T^{\ast }X_P\simeq \mathbb{C}\times X_P$
. Let
$T^{\ast }X_P\simeq \mathbb{C}\times X_P$
. Let
![]() $\Sigma _{E,\theta, Q}$
denote the connected component of
$\Sigma _{E,\theta, Q}$
denote the connected component of
![]() $T^{\ast }X_P\cap \Sigma _{E,\theta }$
which contains
$T^{\ast }X_P\cap \Sigma _{E,\theta }$
which contains
![]() $Q$
. We may assume that
$Q$
. We may assume that
![]() $\Sigma _{E,\theta, Q}\cap T_P^{\ast }X_P=\{Q\}$
and that
$\Sigma _{E,\theta, Q}\cap T_P^{\ast }X_P=\{Q\}$
and that
![]() $\Sigma _{E,\theta, Q}$
is holomorphically isomorphic to a disc. Let
$\Sigma _{E,\theta, Q}$
is holomorphically isomorphic to a disc. Let
![]() $r(Q)$
denote the degree of
$r(Q)$
denote the degree of
![]() $\Sigma _{E,\theta, Q}\to X_P$
. There exist holomorphic functions
$\Sigma _{E,\theta, Q}\to X_P$
. There exist holomorphic functions
![]() $a_j$
$a_j$
![]() $(j=0,\ldots, r(Q)-1)$
on
$(j=0,\ldots, r(Q)-1)$
on
![]() $X_P$
such that
$X_P$
such that
 \begin{align*} \Sigma _{E,\theta, Q} =\left \{ (y,z)\in \mathbb {C}\times X_P\,\left |\, y^{r(Q)}+\sum _{j=0}^{r(Q)-1} a_j(z)y^{j}=0 \right . \right \}. \end{align*}
\begin{align*} \Sigma _{E,\theta, Q} =\left \{ (y,z)\in \mathbb {C}\times X_P\,\left |\, y^{r(Q)}+\sum _{j=0}^{r(Q)-1} a_j(z)y^{j}=0 \right . \right \}. \end{align*}
Because
![]() $T^{\ast }X_P\cap \Sigma _{E,\theta, Q}=\{Q\}$
, there exists
$T^{\ast }X_P\cap \Sigma _{E,\theta, Q}=\{Q\}$
, there exists
![]() $\alpha \in \mathbb{C}$
such that
$\alpha \in \mathbb{C}$
such that
 \begin{align} y^{r(Q)}+\sum _{j=0}^{r(Q)-1} a_j(0)y^j =(y-\alpha )^{r(Q)}. \end{align}
\begin{align} y^{r(Q)}+\sum _{j=0}^{r(Q)-1} a_j(0)y^j =(y-\alpha )^{r(Q)}. \end{align}
The smoothness of
![]() $\Sigma _{E,\theta, Q}$
is equivalent to the condition that
$\Sigma _{E,\theta, Q}$
is equivalent to the condition that
![]() $a_0(z)-(-\alpha )^{r(Q)}$
has a simple
$a_0(z)-(-\alpha )^{r(Q)}$
has a simple
![]() $0$
at
$0$
at
![]() $z=0$
. To study the local property of
$z=0$
. To study the local property of
![]() $\Sigma _{E,\theta, Q}$
around
$\Sigma _{E,\theta, Q}$
around
![]() $Q$
and
$Q$
and
![]() $\theta$
around
$\theta$
around
![]() $P$
, we may assume that
$P$
, we may assume that
![]() $\alpha=0$
by considering
$\alpha=0$
by considering
![]() $\theta _{|X_P}-\alpha dz\,\cdot{\mathop{\textrm{id}}\nolimits }_{E_{|X_P}}$
. Moreover, we may assume that
$\theta _{|X_P}-\alpha dz\,\cdot{\mathop{\textrm{id}}\nolimits }_{E_{|X_P}}$
. Moreover, we may assume that
![]() $a_{r(Q)-1}$
is constantly
$a_{r(Q)-1}$
is constantly
![]() $0$
by considering
$0$
by considering
![]() $\theta _{|X_P}-r(Q)^{-1}a_{r(Q)-1}\,dz\cdot{\mathop{\textrm{id}}\nolimits }_{E_{|X_P}}$
. By changing the coordinate
$\theta _{|X_P}-r(Q)^{-1}a_{r(Q)-1}\,dz\cdot{\mathop{\textrm{id}}\nolimits }_{E_{|X_P}}$
. By changing the coordinate
![]() $z$
to
$z$
to
![]() $w(z)$
satisfying
$w(z)$
satisfying
![]() $w(0)=0$
and
$w(0)=0$
and
![]() $w({\partial }_zw)^{r(Q)}=-a_0(z)$
, we may assume that
$w({\partial }_zw)^{r(Q)}=-a_0(z)$
, we may assume that
![]() $a_0(z)=-z$
. In general,
$a_0(z)=-z$
. In general,
![]() $a_j$
$a_j$
![]() $(1\leqslant j\leqslant r(Q)-2)$
are not constantly
$(1\leqslant j\leqslant r(Q)-2)$
are not constantly
![]() $0$
.
$0$
.
1.2 Main results
1.2.1 The symmetric case
As a first main result, let us mention that if
![]() $(E,\overline{\partial }_E,\theta )$
has a non-degenerate symmetric pairing
$(E,\overline{\partial }_E,\theta )$
has a non-degenerate symmetric pairing
![]() $C$
, then both questions Q1 and Q2 are extremely easy to answer. As explained in [Reference Li and MochizukiLM10b], there exists a unique decoupled harmonic metric
$C$
, then both questions Q1 and Q2 are extremely easy to answer. As explained in [Reference Li and MochizukiLM10b], there exists a unique decoupled harmonic metric
![]() $h^{C}$
of
$h^{C}$
of
![]() $(E,\theta )_{|X\setminus D(E,\theta )}$
which is compatible with
$(E,\theta )_{|X\setminus D(E,\theta )}$
which is compatible with
![]() $C$
. By using a variant of Simpson’s main estimate and an elementary linear algebraic argument in §3.1, we can answer both questions Q1 and Q2, and the limit is
$C$
. By using a variant of Simpson’s main estimate and an elementary linear algebraic argument in §3.1, we can answer both questions Q1 and Q2, and the limit is
![]() $h^{C}$
in this case. The following theorem is a special case of Corollary 3.5.
$h^{C}$
in this case. The following theorem is a special case of Corollary 3.5.
Theorem 1.3.
Let
![]() $K$
be any relatively compact open subset of
$K$
be any relatively compact open subset of
![]() $X\setminus D(E,\theta )$
. Let
$X\setminus D(E,\theta )$
. Let
![]() $s(h^C,h_t)$
denote the automorphism of
$s(h^C,h_t)$
denote the automorphism of
![]() $E_{|X\setminus D(E,\theta )}$
determined by
$E_{|X\setminus D(E,\theta )}$
determined by
![]() $h_t=h^C\cdot s(h^C,h_t)$
. For any
$h_t=h^C\cdot s(h^C,h_t)$
. For any
![]() $\ell \in \mathbb{Z}_{\geqslant 0}$
, there exist positive constants
$\ell \in \mathbb{Z}_{\geqslant 0}$
, there exist positive constants
![]() $C(\ell, K)$
and
$C(\ell, K)$
and
![]() $\epsilon (\ell, K)$
such that the
$\epsilon (\ell, K)$
such that the
![]() $L_{\ell }^2$
-norm of
$L_{\ell }^2$
-norm of
![]() $s(h^C,h_t)-{\mathop{\textrm{id}}\nolimits }$
on
$s(h^C,h_t)-{\mathop{\textrm{id}}\nolimits }$
on
![]() $K$
is dominated by
$K$
is dominated by
![]() $C(\ell, K)\exp (-\epsilon (\ell, K)t)$
as
$C(\ell, K)\exp (-\epsilon (\ell, K)t)$
as
![]() $t\to \infty$
.
$t\to \infty$
.
For example, we may apply this theorem to a Higgs bundle contained in the Hitchin section because it has a canonical non-degenerate symmetric pairing.
Indeed, in Theorem1.3, we do not need to assume that
![]() $X$
is compact. See Theorem3.4 and Corollary 3.5 for the precise statements. These results are also technically useful, which will be applied to the third main result (see §1.2.3 and 1.2.4).
$X$
is compact. See Theorem3.4 and Corollary 3.5 for the precise statements. These results are also technically useful, which will be applied to the third main result (see §1.2.3 and 1.2.4).
1.2.2 The irreducible case
The second main result in this paper is an affirmative answer to question Q1 in the case that the spectral curve is locally and globally irreducible.
We obtain the ideal sheaf
![]() $\mathcal{I}(\Sigma _{E,\theta })\subset \mathcal{O}_{T^{\ast }X}$
of
$\mathcal{I}(\Sigma _{E,\theta })\subset \mathcal{O}_{T^{\ast }X}$
of
![]() $\Sigma _{E,\theta }$
. We say that
$\Sigma _{E,\theta }$
. We say that
![]() $\Sigma _{E,\theta }$
is locally irreducible if the stalks
$\Sigma _{E,\theta }$
is locally irreducible if the stalks
![]() $\mathcal{I}(\Sigma _{E,\theta })_P$
$\mathcal{I}(\Sigma _{E,\theta })_P$
![]() $(P\in \Sigma _{E,\theta })$
are prime ideals. It is equivalent to the condition that for any
$(P\in \Sigma _{E,\theta })$
are prime ideals. It is equivalent to the condition that for any
![]() $P\in \Sigma _{E,\theta }$
the germ of
$P\in \Sigma _{E,\theta }$
the germ of
![]() $\Sigma _{E,\theta }$
at
$\Sigma _{E,\theta }$
at
![]() $P$
cannot be expressed as the union of two distinct germs of non-empty complex analytic subsets. (See [Reference Grauert and RemmertGR84, §4.1].) We say that
$P$
cannot be expressed as the union of two distinct germs of non-empty complex analytic subsets. (See [Reference Grauert and RemmertGR84, §4.1].) We say that
![]() $\Sigma _{E,\theta }$
is globally irreducible if it cannot be expressed as the union of two distinct closed analytic non-empty subsets. The two conditions are independent, in general. Under the assumption that
$\Sigma _{E,\theta }$
is globally irreducible if it cannot be expressed as the union of two distinct closed analytic non-empty subsets. The two conditions are independent, in general. Under the assumption that
![]() $(E,\theta )$
is stable,
$(E,\theta )$
is stable,
![]() $\Sigma _{E,\theta }$
is locally irreducible if and only if it is globally irreducible.
$\Sigma _{E,\theta }$
is locally irreducible if and only if it is globally irreducible.
Theorem 1.4 (Corollary 7.7). Suppose that
![]() $\Sigma _{E,\theta }$
is locally irreducible. Then, the sequence
$\Sigma _{E,\theta }$
is locally irreducible. Then, the sequence
![]() $h_t$
is convergent to a decoupled harmonic metric
$h_t$
is convergent to a decoupled harmonic metric
![]() $h_{\infty }$
in the
$h_{\infty }$
in the
![]() $C^{\infty }$
-sense locally on
$C^{\infty }$
-sense locally on
![]() $X\setminus D(E,\theta )$
.
$X\setminus D(E,\theta )$
.
See Theorem7.5 for the more general statement.
More precisely, we canonically construct a filtered bundle
![]() $\mathcal{P}^{\star }_{\ast }(\mathcal{V})$
over
$\mathcal{P}^{\star }_{\ast }(\mathcal{V})$
over
![]() $\mathcal{V}=E(\ast D(E,\theta ))$
in an algebraic way from
$\mathcal{V}=E(\ast D(E,\theta ))$
in an algebraic way from
![]() $(E,\theta )$
such that (i)
$(E,\theta )$
such that (i)
![]() $(\mathcal{P}^{\star }_{\ast }(\mathcal{V}),\theta )$
is a decomposable filtered Higgs bundle in the sense of Definition 5.10, (ii)
$(\mathcal{P}^{\star }_{\ast }(\mathcal{V}),\theta )$
is a decomposable filtered Higgs bundle in the sense of Definition 5.10, (ii)
![]() $(\mathcal{P}^{\star }_{\ast }(\mathcal{V}),\theta )$
is stable of degree
$(\mathcal{P}^{\star }_{\ast }(\mathcal{V}),\theta )$
is stable of degree
![]() $0$
and (iii)
$0$
and (iii)
![]() $\det (\mathcal{P}^{\star }_{\ast }\mathcal{V})$
equals the filtered bundle naturally induced by
$\det (\mathcal{P}^{\star }_{\ast }\mathcal{V})$
equals the filtered bundle naturally induced by
![]() $\det (E)$
. There exists a unique decoupled harmonic metric
$\det (E)$
. There exists a unique decoupled harmonic metric
![]() $h_{\infty }$
of
$h_{\infty }$
of
![]() $(E,\theta )_{|X\setminus D(E,\theta )}$
adapted to
$(E,\theta )_{|X\setminus D(E,\theta )}$
adapted to
![]() $\mathcal{P}^{\star }_{\ast }(\mathcal{V})$
such that
$\mathcal{P}^{\star }_{\ast }(\mathcal{V})$
such that
![]() $\det (h_{\infty })=h_{\det (E)}$
. We shall prove that the sequence
$\det (h_{\infty })=h_{\det (E)}$
. We shall prove that the sequence
![]() $h_t$
is convergent to
$h_t$
is convergent to
![]() $h_{\infty }$
as
$h_{\infty }$
as
![]() $t\to \infty$
on
$t\to \infty$
on
![]() $X\setminus D(E,\theta )$
.
$X\setminus D(E,\theta )$
.
An outline of the proof is as follows. Let
![]() $P\in D(E,\theta )$
. Let
$P\in D(E,\theta )$
. Let
![]() $X_P$
be a small neighbourhood of
$X_P$
be a small neighbourhood of
![]() $P$
in
$P$
in
![]() $X$
. By a theorem of Donaldson [Reference DonaldsonDon92], there exists a harmonic metric
$X$
. By a theorem of Donaldson [Reference DonaldsonDon92], there exists a harmonic metric
![]() $h_{P,t}$
of
$h_{P,t}$
of
![]() $(E,\overline{\partial },t\theta )_{|X_P}$
such that
$(E,\overline{\partial },t\theta )_{|X_P}$
such that
![]() $h_{P,t|{\partial } X_P}=h_{\infty |{\partial } X_P}$
. According to Proposition 6.6, the sequence
$h_{P,t|{\partial } X_P}=h_{\infty |{\partial } X_P}$
. According to Proposition 6.6, the sequence
![]() $h_{P,t}$
is convergent to
$h_{P,t}$
is convergent to
![]() $h_{\infty |X_P\setminus \{P\}}$
in the
$h_{\infty |X_P\setminus \{P\}}$
in the
![]() $C^{\infty }$
-sense locally on
$C^{\infty }$
-sense locally on
![]() $X_P\setminus \{P\}$
as
$X_P\setminus \{P\}$
as
![]() $t\to \infty$
. As in [Reference Mazzeo, Swoboda, Weiss and WittMSW16], by patching
$t\to \infty$
. As in [Reference Mazzeo, Swoboda, Weiss and WittMSW16], by patching
![]() $h_{P,t}$
and
$h_{P,t}$
and
![]() $h_{\infty }$
, we construct a family of Hermitian metrics
$h_{\infty }$
, we construct a family of Hermitian metrics
![]() $\widetilde{h}_t$
$\widetilde{h}_t$
![]() $(t\gt 0)$
of
$(t\gt 0)$
of
![]() $E$
such that (i)
$E$
such that (i)
![]() $\det (\widetilde{h}_t)=h_{\det (E)}$
, (ii)
$\det (\widetilde{h}_t)=h_{\det (E)}$
, (ii)
![]() $\lim _{t\to \infty }\widetilde{h}_t=h_{\infty }$
on
$\lim _{t\to \infty }\widetilde{h}_t=h_{\infty }$
on
![]() $X\setminus D(E,\theta )$
and (iii)
$X\setminus D(E,\theta )$
and (iii)
![]() $\int _X \bigl | R(\widetilde{h}_t) +\bigl [ t\theta, (t\theta )^{\dagger }_{\widetilde{h}_t} \bigr ]\bigr |\to 0$
. Let
$\int _X \bigl | R(\widetilde{h}_t) +\bigl [ t\theta, (t\theta )^{\dagger }_{\widetilde{h}_t} \bigr ]\bigr |\to 0$
. Let
![]() $s(\widetilde{h}_t,h_t)$
denote the automorphism of
$s(\widetilde{h}_t,h_t)$
denote the automorphism of
![]() $E$
determined by
$E$
determined by
![]() $h_t=\widetilde{h}_t\cdot s(\widetilde{h}_t,h_t)$
. Then, we shall prove that
$h_t=\widetilde{h}_t\cdot s(\widetilde{h}_t,h_t)$
. Then, we shall prove that
![]() $\sup _X(s(\widetilde{h}_t,h_t)-{\mathop{\textrm{id}}\nolimits }_E)\to 0$
by essentially the same argument as that in [Reference MochizukiMoc16].
$\sup _X(s(\widetilde{h}_t,h_t)-{\mathop{\textrm{id}}\nolimits }_E)\to 0$
by essentially the same argument as that in [Reference MochizukiMoc16].
Because of the assumption of the local irreducibility of
![]() $\Sigma _{E,\theta }$
, it is easy to find the candidate of ‘the limiting configuration’
$\Sigma _{E,\theta }$
, it is easy to find the candidate of ‘the limiting configuration’
![]() $h_{\infty }$
. In the rank two case, the Higgs bundle
$h_{\infty }$
. In the rank two case, the Higgs bundle
![]() $(E,\theta )_{|X_P}$
is easy to understand. There is a homogeneous wild harmonic bundle
$(E,\theta )_{|X_P}$
is easy to understand. There is a homogeneous wild harmonic bundle
![]() $(E'_P,\theta '_P,h'_P)$
on
$(E'_P,\theta '_P,h'_P)$
on
![]() $(\mathbb{P}^1,\infty )$
such that the restriction of
$(\mathbb{P}^1,\infty )$
such that the restriction of
![]() $(E'_P,\theta '_P)$
to a neighbourhood of
$(E'_P,\theta '_P)$
to a neighbourhood of
![]() $0$
is isomorphic to
$0$
is isomorphic to
![]() $(E,\theta )_{|X_P}$
, where we consider an
$(E,\theta )_{|X_P}$
, where we consider an
![]() $S^1$
-action on
$S^1$
-action on
![]() $\mathbb{P}^1$
induced by
$\mathbb{P}^1$
induced by
![]() $(a,z)\mapsto a^mz$
for some
$(a,z)\mapsto a^mz$
for some
![]() $m\in \mathbb{Z}_{\gt 0}$
. (See [Reference MochizukiMoc21, §8] for homogeneity of harmonic bundles with respect to an
$m\in \mathbb{Z}_{\gt 0}$
. (See [Reference MochizukiMoc21, §8] for homogeneity of harmonic bundles with respect to an
![]() $S^1$
-action.) The special case is a fiducial solution in [Reference Mazzeo, Swoboda, Weiss and WittMSW16]. In [Reference MochizukiMoc16], the restriction of
$S^1$
-action.) The special case is a fiducial solution in [Reference Mazzeo, Swoboda, Weiss and WittMSW16]. In [Reference MochizukiMoc16], the restriction of
![]() $h'_P$
was useful in the construction of approximate solutions
$h'_P$
was useful in the construction of approximate solutions
![]() $\widetilde{h}_t$
. In the higher rank case, the Higgs bundle
$\widetilde{h}_t$
. In the higher rank case, the Higgs bundle
![]() $(E,\theta )_{|X_P}$
is more complicated even under the assumption of local irreducibility. It does not seem that the approximation by a homogeneous wild harmonic bundle can work well. Therefore, we develop a way to use the solutions of the boundary-value problem in the construction of approximate solutions.
$(E,\theta )_{|X_P}$
is more complicated even under the assumption of local irreducibility. It does not seem that the approximation by a homogeneous wild harmonic bundle can work well. Therefore, we develop a way to use the solutions of the boundary-value problem in the construction of approximate solutions.
Remark 1.5. Because we also study the question
![]() $\textbf{Q1}$
for wild harmonic bundles under a similar assumption on the spectral curve, we also study the Dirichlet problem for wild harmonic bundles (Theorem 2.8).
$\textbf{Q1}$
for wild harmonic bundles under a similar assumption on the spectral curve, we also study the Dirichlet problem for wild harmonic bundles (Theorem 2.8).
1.2.3 The order of convergence in the smooth case
We study question Q2 under the following additional condition.
Condition 1.6.
Let
![]() $\rho :\widetilde{\Sigma }_{E,\theta }\to \Sigma _{E,\theta }$
be the normalization. There exists a holomorphic line bundle
$\rho :\widetilde{\Sigma }_{E,\theta }\to \Sigma _{E,\theta }$
be the normalization. There exists a holomorphic line bundle
![]() $L$
with an isomorphism
$L$
with an isomorphism
![]() $E\simeq (\pi \circ \rho )_{\ast }L$
such that
$E\simeq (\pi \circ \rho )_{\ast }L$
such that
![]() $\theta$
is induced by the
$\theta$
is induced by the
![]() $\mathcal{O}_{T^{\ast }X}$
-action on
$\mathcal{O}_{T^{\ast }X}$
-action on
![]() $\rho _{\ast }L$
.
$\rho _{\ast }L$
.
For example, this condition is satisfied if
![]() $\Sigma _{E,\theta }$
is smooth according to [Reference Beauville, Narasimhan and RamananBNR89, Reference HitchinHit87]. We shall prove the following theorem.
$\Sigma _{E,\theta }$
is smooth according to [Reference Beauville, Narasimhan and RamananBNR89, Reference HitchinHit87]. We shall prove the following theorem.
Theorem 1.7 (Theorem7.14). Suppose that Condition 1.6 is satisfied. Let
![]() $s(h_{\infty },h_{t})$
be the automorphism of
$s(h_{\infty },h_{t})$
be the automorphism of
![]() $(E,\theta )_{|X\setminus D(E,\theta )}$
determined by
$(E,\theta )_{|X\setminus D(E,\theta )}$
determined by
![]() $h_t=h_{\infty }\cdot s(h_{\infty },h_t)$
. Let
$h_t=h_{\infty }\cdot s(h_{\infty },h_t)$
. Let
![]() $K\subset X\setminus D(E,\theta )$
be any relatively compact open subset. For any
$K\subset X\setminus D(E,\theta )$
be any relatively compact open subset. For any
![]() $\ell \in \mathbb{Z}_{\geqslant 0}$
, there exist
$\ell \in \mathbb{Z}_{\geqslant 0}$
, there exist
![]() $C(\ell, K)\gt 0$
and
$C(\ell, K)\gt 0$
and
![]() $\epsilon (\ell, K)\gt 0$
such that the following holds as
$\epsilon (\ell, K)\gt 0$
such that the following holds as
![]() $t\to \infty$
:
$t\to \infty$
:
To prove Theorem1.7, we refine the construction of
![]() $\widetilde{h}_t$
in §1.2.2. For each
$\widetilde{h}_t$
in §1.2.2. For each
![]() $P\in D(E,\theta )$
, there exists a non-degenerate symmetric pairing
$P\in D(E,\theta )$
, there exists a non-degenerate symmetric pairing
![]() $C_P$
of
$C_P$
of
![]() $(E,\overline{\partial }_E,\theta )_{|X_P}$
such that
$(E,\overline{\partial }_E,\theta )_{|X_P}$
such that
![]() $C_{P|X_P\setminus \{P\}}$
is compatible with
$C_{P|X_P\setminus \{P\}}$
is compatible with
![]() $h_{\infty |X_P\setminus \{P\}}$
. It is easy to see that the harmonic metric
$h_{\infty |X_P\setminus \{P\}}$
. It is easy to see that the harmonic metric
![]() $h_{P,t}$
of
$h_{P,t}$
of
![]() $(E,\theta )_{|X_P}$
satisfying
$(E,\theta )_{|X_P}$
satisfying
![]() $h_{P,t|{\partial } X_P}=h_{\infty |{\partial } X_P}$
is compatible with
$h_{P,t|{\partial } X_P}=h_{\infty |{\partial } X_P}$
is compatible with
![]() $C_{P}$
. Let
$C_{P}$
. Let
![]() $s(h_{\infty },h_{P,t})$
be the automorphism of
$s(h_{\infty },h_{P,t})$
be the automorphism of
![]() $E_{|X_P\setminus \{P\}}$
determined by
$E_{|X_P\setminus \{P\}}$
determined by
![]() $h_{P,t}=h_{\infty |X_P\setminus \{P\}}\cdot s(h_{\infty },h_{P,t})$
. By the result in the symmetric case mentioned in §1.2.1, on any relatively compact open subset
$h_{P,t}=h_{\infty |X_P\setminus \{P\}}\cdot s(h_{\infty },h_{P,t})$
. By the result in the symmetric case mentioned in §1.2.1, on any relatively compact open subset
![]() $K$
of
$K$
of
![]() $X_P\setminus \{P\}$
,
$X_P\setminus \{P\}$
,
![]() $s(h_{\infty },h_{P,t})-{\mathop{\textrm{id}}\nolimits }$
converges to
$s(h_{\infty },h_{P,t})-{\mathop{\textrm{id}}\nolimits }$
converges to
![]() $0$
at a speed of the order of
$0$
at a speed of the order of
![]() $e^{-\delta (K)t}$
. Then, the following stronger condition is satisfied:
$e^{-\delta (K)t}$
. Then, the following stronger condition is satisfied:
Then, we can obtain the estimate of
![]() $\sup |s(\widetilde{h}_t,h_t)-{\mathop{\textrm{id}}\nolimits }|$
on any relatively compact open subset in
$\sup |s(\widetilde{h}_t,h_t)-{\mathop{\textrm{id}}\nolimits }|$
on any relatively compact open subset in
![]() $X\setminus D(E,\theta )$
. By a general argument in §4.2, we can obtain the desired estimate of the norms of
$X\setminus D(E,\theta )$
. By a general argument in §4.2, we can obtain the desired estimate of the norms of
![]() $s(\widetilde{h}_t,h_t)-{\mathop{\textrm{id}}\nolimits }$
and its higher derivatives on
$s(\widetilde{h}_t,h_t)-{\mathop{\textrm{id}}\nolimits }$
and its higher derivatives on
![]() $X$
even around
$X$
even around
![]() $D(E,\theta )$
.
$D(E,\theta )$
.
1.2.4 A family case
The result and the method in §1.2.3 can be generalized to the following family case. Let
![]() $p_1:\widetilde{\mathcal{X}}\to \mathcal{S}$
be a smooth proper morphism of complex manifolds such that each fiber is connected and
$p_1:\widetilde{\mathcal{X}}\to \mathcal{S}$
be a smooth proper morphism of complex manifolds such that each fiber is connected and
![]() $1$
-dimensional. We also assume that
$1$
-dimensional. We also assume that
![]() $\mathcal{S}$
is connected. Let
$\mathcal{S}$
is connected. Let
![]() $\pi :\mathcal{S}\times T^{\ast }X\to \mathcal{S}\times X$
and
$\pi :\mathcal{S}\times T^{\ast }X\to \mathcal{S}\times X$
and
![]() $p_2:\mathcal{S}\times X\to \mathcal{S}$
denote the projections. Let
$p_2:\mathcal{S}\times X\to \mathcal{S}$
denote the projections. Let
![]() $\Phi _0:\widetilde{\mathcal{X}}\to \mathcal{S}\times T^{\ast }X$
be a morphism of complex manifolds such that
$\Phi _0:\widetilde{\mathcal{X}}\to \mathcal{S}\times T^{\ast }X$
be a morphism of complex manifolds such that
![]() $p_2\circ \pi \circ \Phi _0=p_1$
. We set
$p_2\circ \pi \circ \Phi _0=p_1$
. We set
![]() $\Phi _1:=\pi \circ \Phi _0:\widetilde{\mathcal{X}}\to \mathcal{S}\times X$
. We assume the following.
$\Phi _1:=\pi \circ \Phi _0:\widetilde{\mathcal{X}}\to \mathcal{S}\times X$
. We assume the following.
-
–
 $\Phi _1$
is proper and finite.
$\Phi _1$
is proper and finite. -
– There exists a closed complex analytic hypersurface
 $\mathcal{D}\subset \mathcal{S}\times X$
such that (i)
$\mathcal{D}\subset \mathcal{S}\times X$
such that (i)
 $\mathcal{D}$
is finite over
$\mathcal{D}$
is finite over
 $\mathcal{S}$
, (ii) the induced map
$\mathcal{S}$
, (ii) the induced map
 $\widetilde{\mathcal{X}}\setminus \Phi _1^{-1}(\mathcal{D}) \longrightarrow (\mathcal{S}\times X)\setminus \mathcal{D}$
is a covering map, and (iii)
$\widetilde{\mathcal{X}}\setminus \Phi _1^{-1}(\mathcal{D}) \longrightarrow (\mathcal{S}\times X)\setminus \mathcal{D}$
is a covering map, and (iii)
 $\Phi _0$
induces an injection
$\Phi _0$
induces an injection
 $\widetilde{\mathcal{X}}\setminus \Phi _1^{-1}(\mathcal{D}) \longrightarrow \mathcal{S}\times T^{\ast }X$
.
$\widetilde{\mathcal{X}}\setminus \Phi _1^{-1}(\mathcal{D}) \longrightarrow \mathcal{S}\times T^{\ast }X$
.
We set
![]() $r:=|\Phi _1^{-1}(P)|$
for any
$r:=|\Phi _1^{-1}(P)|$
for any
![]() $P\in (\mathcal{S}\times X)\setminus \mathcal{D}$
. Let
$P\in (\mathcal{S}\times X)\setminus \mathcal{D}$
. Let
![]() $g(X)$
and
$g(X)$
and
![]() $\widetilde{g}$
denote the genus of
$\widetilde{g}$
denote the genus of
![]() $X$
and
$X$
and
![]() $p_1^{-1}(x)$
$p_1^{-1}(x)$
![]() $(x\in \mathcal{S})$
, respectively. We set
$(x\in \mathcal{S})$
, respectively. We set
![]() $X_x=\{x\}\times X$
and
$X_x=\{x\}\times X$
and
![]() $\mathcal{D}_{x}=\mathcal{D}\cap X_x$
. There exists a natural isomorphism
$\mathcal{D}_{x}=\mathcal{D}\cap X_x$
. There exists a natural isomorphism
![]() $X_x\simeq X$
. We note that
$X_x\simeq X$
. We note that
![]() $\mathcal{D}\to \mathcal{S}$
is not assumed to be a covering map, and hence
$\mathcal{D}\to \mathcal{S}$
is not assumed to be a covering map, and hence
![]() $|\mathcal{D}_{x}|$
is not necessarily constant on
$|\mathcal{D}_{x}|$
is not necessarily constant on
![]() $\mathcal{S}$
.
$\mathcal{S}$
.
Let
![]() $\mathcal{L}$
be a holomorphic line bundle on
$\mathcal{L}$
be a holomorphic line bundle on
![]() $\widetilde{\mathcal{X}}$
such that
$\widetilde{\mathcal{X}}$
such that
![]() $\deg (\mathcal{L}_{|p_1^{-1}(x)})= \widetilde{g}-rg(X)+r-1$
. We obtain a locally free
$\deg (\mathcal{L}_{|p_1^{-1}(x)})= \widetilde{g}-rg(X)+r-1$
. We obtain a locally free
![]() $\mathcal{O}_{\mathcal{S}\times X}$
-module
$\mathcal{O}_{\mathcal{S}\times X}$
-module
![]() $\mathcal{E}=\Phi _{1\ast }(\mathcal{L})$
. It is equipped with the morphism
$\mathcal{E}=\Phi _{1\ast }(\mathcal{L})$
. It is equipped with the morphism
![]() $\theta : \mathcal{E}\to \mathcal{E}\otimes \Omega^1_{\mathcal{S}\times X/\mathcal{S}}$
induced by the
$\theta : \mathcal{E}\to \mathcal{E}\otimes \Omega^1_{\mathcal{S}\times X/\mathcal{S}}$
induced by the
![]() $\mathcal{O}_{\mathcal{S}\times T^{\ast }X}$
-action on
$\mathcal{O}_{\mathcal{S}\times T^{\ast }X}$
-action on
![]() $\Phi _{0\ast }\mathcal{L}$
. For each
$\Phi _{0\ast }\mathcal{L}$
. For each
![]() $x\in \mathcal{S}$
, we obtain the Higgs bundle
$x\in \mathcal{S}$
, we obtain the Higgs bundle
![]() $(\mathcal{E}_x,\theta _x)=(\mathcal{E},\theta )_{|X_x}$
, which is stable of degree
$(\mathcal{E}_x,\theta _x)=(\mathcal{E},\theta )_{|X_x}$
, which is stable of degree
![]() $0$
.
$0$
.
There exists a Hermitian metric
![]() $h_{\det \mathcal{E}}$
of
$h_{\det \mathcal{E}}$
of
![]() $\det (\mathcal{E})$
such that
$\det (\mathcal{E})$
such that
![]() $h_{\det \mathcal{E}|X_x}$
are flat for any
$h_{\det \mathcal{E}|X_x}$
are flat for any
![]() $x\in \mathcal{S}$
. There exist harmonic metrics
$x\in \mathcal{S}$
. There exist harmonic metrics
![]() $h_{t,x}$
of
$h_{t,x}$
of
![]() $(\mathcal{E}_x,t\theta _x)$
$(\mathcal{E}_x,t\theta _x)$
![]() $(x\in \mathcal{S})$
such that
$(x\in \mathcal{S})$
such that
![]() $\det (h_{t,x})=h_{\det \mathcal{E}|X_x}$
. There also exist decoupled harmonic metrics
$\det (h_{t,x})=h_{\det \mathcal{E}|X_x}$
. There also exist decoupled harmonic metrics
![]() $h_{\infty, x}$
$h_{\infty, x}$
![]() $(x\in \mathcal{S})$
of
$(x\in \mathcal{S})$
of
![]() $(\mathcal{E}_x,\theta _x)_{|X_x\setminus \mathcal{D}_{x}}$
such that
$(\mathcal{E}_x,\theta _x)_{|X_x\setminus \mathcal{D}_{x}}$
such that
![]() $\det (h_{\infty, x})=h_{\det (\mathcal{E})|X_x\setminus \mathcal{D}_x}$
.
$\det (h_{\infty, x})=h_{\det (\mathcal{E})|X_x\setminus \mathcal{D}_x}$
.
Theorem 1.8 (Theorem7.22). Let
![]() $x_0\in \mathcal{S}$
. Let
$x_0\in \mathcal{S}$
. Let
![]() $K$
be a relatively compact open subset of
$K$
be a relatively compact open subset of
![]() $X_{x_0}\setminus \mathcal{D}_{x_0}$
. Let
$X_{x_0}\setminus \mathcal{D}_{x_0}$
. Let
![]() $\mathcal{S}_0$
be a neighbourhood of
$\mathcal{S}_0$
be a neighbourhood of
![]() $x_0$
in
$x_0$
in
![]() $\mathcal{S}$
such that
$\mathcal{S}$
such that
![]() $\mathcal{S}_0\times K$
is relatively compact in
$\mathcal{S}_0\times K$
is relatively compact in
![]() $(\mathcal{S}\times X)\setminus \mathcal{D}$
. For any
$(\mathcal{S}\times X)\setminus \mathcal{D}$
. For any
![]() $\ell \in \mathbb{Z}_{\geqslant 0}$
, there exist
$\ell \in \mathbb{Z}_{\geqslant 0}$
, there exist
![]() $C(\ell ),\epsilon (\ell )\gt 0$
such that the
$C(\ell ),\epsilon (\ell )\gt 0$
such that the
![]() $L_{\ell }^2$
-norm of
$L_{\ell }^2$
-norm of
![]() $s(h_{\infty, x},h_{t,x})-{\mathop{\textrm{id}}\nolimits }$
$s(h_{\infty, x},h_{t,x})-{\mathop{\textrm{id}}\nolimits }$
![]() $(x\in \mathcal{S}_0,t\geqslant 1)$
on
$(x\in \mathcal{S}_0,t\geqslant 1)$
on
![]() $K$
are dominated by
$K$
are dominated by
![]() $C(\ell )\exp (-\epsilon (\ell )t)$
.
$C(\ell )\exp (-\epsilon (\ell )t)$
.
Remark 1.9. Note that for another Hermitian metric
![]() $h'_{\det \mathcal{E}}$
of
$h'_{\det \mathcal{E}}$
of
![]() $\det (\mathcal{E})$
such that
$\det (\mathcal{E})$
such that
![]() $h'_{\det \mathcal{E}|X_x}$
are flat for any
$h'_{\det \mathcal{E}|X_x}$
are flat for any
![]() $x\in \mathcal{S}$
, we obtain an
$x\in \mathcal{S}$
, we obtain an
![]() $\mathbb{R}_{\gt 0}$
-valued
$\mathbb{R}_{\gt 0}$
-valued
![]() $C^{\infty }$
-function
$C^{\infty }$
-function
![]() $\beta$
on
$\beta$
on
![]() $\mathcal{S}$
determined by
$\mathcal{S}$
determined by
![]() $h'_{\det (\mathcal{E})}=\beta h_{\det (\mathcal{E})}$
, and
$h'_{\det (\mathcal{E})}=\beta h_{\det (\mathcal{E})}$
, and
![]() $\beta ^{1/r}h_{t,x}$
(respectively
$\beta ^{1/r}h_{t,x}$
(respectively
![]() $\beta ^{1/r}h_{\infty, x}$
) are harmonic metrics (respectively decoupled harmonic metrics) of
$\beta ^{1/r}h_{\infty, x}$
) are harmonic metrics (respectively decoupled harmonic metrics) of
![]() $(\mathcal{E}_x,t\theta _x)$
(respectively
$(\mathcal{E}_x,t\theta _x)$
(respectively
![]() $(\mathcal{E}_x,\theta _x)_{|X_x\setminus \mathcal{D}_x}$
) such that
$(\mathcal{E}_x,\theta _x)_{|X_x\setminus \mathcal{D}_x}$
) such that
![]() $\det (\beta ^{1/r}h_{t,x})=h'_{\det \mathcal{E}|X_x}$
(respectively
$\det (\beta ^{1/r}h_{t,x})=h'_{\det \mathcal{E}|X_x}$
(respectively
![]() $\det (\beta ^{1/r}h_{\infty, x})= h'_{\det (\mathcal{E})|X_x\setminus \mathcal{D}_x}$
). Hence, the claim of Theorem 1.8 is independent of the choice of
$\det (\beta ^{1/r}h_{\infty, x})= h'_{\det (\mathcal{E})|X_x\setminus \mathcal{D}_x}$
). Hence, the claim of Theorem 1.8 is independent of the choice of
![]() $h_{\det \mathcal{E}}$
.
$h_{\det \mathcal{E}}$
.
Remark 1.10. We may apply Theorem 1.8 to obtain a locally uniform estimate for large-scale solutions of the Hitchin equation for a family of stable Higgs bundles of degree
![]() $0$
whose spectral curves are smooth.
$0$
whose spectral curves are smooth.
2. Preliminaries
2.1 Some definitions
2.1.1 Decoupled harmonic bundles
Let
![]() $Y$
be a Riemann surface. Let
$Y$
be a Riemann surface. Let
![]() $(V,\theta )$
be a Higgs bundle on
$(V,\theta )$
be a Higgs bundle on
![]() $Y$
.
$Y$
.
Definition 2.1. A Hermitian metric
![]() $h$
of
$h$
of
![]() $V$
is called a decoupled harmonic metric of
$V$
is called a decoupled harmonic metric of
![]() $(V,\theta )$
if the following conditions are satisfied.
$(V,\theta )$
if the following conditions are satisfied.
-
(A1)
 $h$
is a harmonic metric of the Higgs bundle
$h$
is a harmonic metric of the Higgs bundle
 $(V,\overline{\partial }_V,\theta )$
.
$(V,\overline{\partial }_V,\theta )$
. -
(A2)
 $h$
is flat, i.e. the Chern connection
$h$
is flat, i.e. the Chern connection
 $\nabla _h$
of
$\nabla _h$
of
 $(V,\overline{\partial }_V,h)$
is flat.
$(V,\overline{\partial }_V,h)$
is flat.
Such a
![]() $(V,\theta, h)$
is called a decoupled harmonic bundle.
$(V,\theta, h)$
is called a decoupled harmonic bundle.
Note that the conditions (A1) and (A2) imply that
![]() $\theta$
and
$\theta$
and
![]() $\theta ^{\dagger }_h$
are commuting.
$\theta ^{\dagger }_h$
are commuting.
2.1.2 Symmetric Higgs bundles
Let
![]() $C$
be a non-degenerate symmetric product of
$C$
be a non-degenerate symmetric product of
![]() $V$
. It is called a non-degenerate symmetric product of the Higgs bundle
$V$
. It is called a non-degenerate symmetric product of the Higgs bundle
![]() $(V,\theta )$
if
$(V,\theta )$
if
![]() $\theta$
is self-adjoint with respect to
$\theta$
is self-adjoint with respect to
![]() $C$
. Such a tuple
$C$
. Such a tuple
![]() $(V,\theta, C)$
is called a symmetric Higgs bundle. Let
$(V,\theta, C)$
is called a symmetric Higgs bundle. Let
![]() $V^{\lor }$
denote the dual bundle of
$V^{\lor }$
denote the dual bundle of
![]() $V$
. Let
$V$
. Let
![]() $\Psi _C:V\to V^{\lor }$
be the isomorphism induced by
$\Psi _C:V\to V^{\lor }$
be the isomorphism induced by
![]() $C$
. Let
$C$
. Let
![]() $\theta ^{\lor }$
be the induced Higgs field of
$\theta ^{\lor }$
be the induced Higgs field of
![]() $V^{\lor }$
. The condition is equivalent to
$V^{\lor }$
. The condition is equivalent to
![]() $\Psi _C$
inducing an isomorphism of the Higgs bundles
$\Psi _C$
inducing an isomorphism of the Higgs bundles
![]() $(V,\theta )\simeq (V^{\lor },\theta ^{\lor })$
.
$(V,\theta )\simeq (V^{\lor },\theta ^{\lor })$
.
A Hermitian metric
![]() $h$
of
$h$
of
![]() $V$
is said to be compatible with
$V$
is said to be compatible with
![]() $C$
if
$C$
if
![]() $\Psi _C$
is isometric with respect to
$\Psi _C$
is isometric with respect to
![]() $h$
and its dual Hermitian metric
$h$
and its dual Hermitian metric
![]() $h^{\lor }$
of
$h^{\lor }$
of
![]() $V^{\lor }$
.
$V^{\lor }$
.
2.1.3 Generically regular semisimple Higgs bundles
Let
![]() $\Sigma _{V,\theta }\subset T^{\ast }Y$
denote the spectral curve of
$\Sigma _{V,\theta }\subset T^{\ast }Y$
denote the spectral curve of
![]() $(V,\theta )$
. We say that
$(V,\theta )$
. We say that
![]() $(V,\theta )$
is regular semisimple if the projection
$(V,\theta )$
is regular semisimple if the projection
![]() $\Sigma _{V,\theta }\to Y$
is a covering map. We say that
$\Sigma _{V,\theta }\to Y$
is a covering map. We say that
![]() $(V,\theta )$
is generically regular semisimple if there exists a discrete subset
$(V,\theta )$
is generically regular semisimple if there exists a discrete subset
![]() $D\subset Y$
such that
$D\subset Y$
such that
![]() $(V,\theta )_{|Y\setminus D}$
is regular semisimple.
$(V,\theta )_{|Y\setminus D}$
is regular semisimple.
Let
![]() $\pi :\Sigma _{V,\theta }\to Y$
denote the projection. If
$\pi :\Sigma _{V,\theta }\to Y$
denote the projection. If
![]() $(V,\theta )$
is regular semisimple, there exists a line bundle
$(V,\theta )$
is regular semisimple, there exists a line bundle
![]() $L_V$
on
$L_V$
on
![]() $\Sigma _{V,\theta }$
with an isomorphism
$\Sigma _{V,\theta }$
with an isomorphism
![]() $\pi _{\ast }L_V\simeq V$
such that
$\pi _{\ast }L_V\simeq V$
such that
![]() $\theta$
is induced by
$\theta$
is induced by
![]() $\mathcal{O}_{T^{\ast }Y}$
-action on
$\mathcal{O}_{T^{\ast }Y}$
-action on
![]() $L_V$
.
$L_V$
.
2.2 Regular semisimple case
2.2.1 Decoupled harmonic metrics
Suppose that
![]() $(V,\theta )$
is regular semisimple. We consider the following condition for a Hermitian metric
$(V,\theta )$
is regular semisimple. We consider the following condition for a Hermitian metric
![]() $h$
of
$h$
of
![]() $V$
.
$V$
.
-
(A3) For any
 $P\in Y$
, the eigen decomposition of
$P\in Y$
, the eigen decomposition of
 $\theta$
at
$\theta$
at
 $P$
is orthogonal with respect to
$P$
is orthogonal with respect to
 $h$
.
$h$
.
Note that (A3) holds if and only if
![]() $\theta$
and
$\theta$
and
![]() $\theta ^{\dagger }_h$
are commuting. The following lemma is easy to see.
$\theta ^{\dagger }_h$
are commuting. The following lemma is easy to see.
Lemma 2.2.
If two of the conditions (A1), (A2), and (A3) are satisfied for a Hermitian metric
![]() $h$
of
$h$
of
![]() $V$
, then
$V$
, then
![]() $h$
is a decoupled harmonic metric of
$h$
is a decoupled harmonic metric of
![]() $(V,\theta )$
.
$(V,\theta )$
.
A flat metric
![]() $h_{L_V}$
of
$h_{L_V}$
of
![]() $L_V$
induces a Hermitian metric
$L_V$
induces a Hermitian metric
![]() $\pi _{\ast }(h_{L_V})$
of
$\pi _{\ast }(h_{L_V})$
of
![]() $V$
. It is easy to check that
$V$
. It is easy to check that
![]() $\pi _{\ast }(h_{L_V})$
is a decoupled harmonic metric of
$\pi _{\ast }(h_{L_V})$
is a decoupled harmonic metric of
![]() $(V,\theta )$
.
$(V,\theta )$
.
Proposition 2.3.
This procedure induces an equivalence between flat metrics of
![]() $L_V$
and decoupled harmonic metrics of
$L_V$
and decoupled harmonic metrics of
![]() $(V,\theta )$
.
$(V,\theta )$
.
Remark 2.4. Let
![]() $(V,\theta, h)$
be a decoupled harmonic bundle. Let
$(V,\theta, h)$
be a decoupled harmonic bundle. Let
![]() $\Sigma _{V,\theta }=\coprod _{i\in \Lambda }\Sigma _{V,\theta, i}$
be the decomposition into connected components. There exists the corresponding decomposition of the Higgs bundle
$\Sigma _{V,\theta }=\coprod _{i\in \Lambda }\Sigma _{V,\theta, i}$
be the decomposition into connected components. There exists the corresponding decomposition of the Higgs bundle
![]() $(V,\theta )=\bigoplus _{i\in \Lambda }(V_i,\theta _i)$
such that
$(V,\theta )=\bigoplus _{i\in \Lambda }(V_i,\theta _i)$
such that
![]() $\Sigma _{V_i,\theta _i}=\Sigma _{V,\theta, i}$
. Because
$\Sigma _{V_i,\theta _i}=\Sigma _{V,\theta, i}$
. Because
![]() $h$
is a decoupled harmonic metric, the decomposition is orthogonal with respect to
$h$
is a decoupled harmonic metric, the decomposition is orthogonal with respect to
![]() $h$
. Hence, we obtain the decomposition of a decoupled harmonic bundle
$h$
. Hence, we obtain the decomposition of a decoupled harmonic bundle
![]() $(V,\theta, h)=\bigoplus (V_i,\theta _i,h_i)$
.
$(V,\theta, h)=\bigoplus (V_i,\theta _i,h_i)$
.
2.2.2 Symmetric products
The multiplication of
![]() $\mathcal{O}_{\Sigma _{V,\theta }}$
induces a multiplication
$\mathcal{O}_{\Sigma _{V,\theta }}$
induces a multiplication
Any local section
![]() $f$
of
$f$
of
![]() $\pi _{\ast }\mathcal{O}_{\Sigma _{V,\theta }}$
induces an endomorphism
$\pi _{\ast }\mathcal{O}_{\Sigma _{V,\theta }}$
induces an endomorphism
![]() $F_f$
of the locally free
$F_f$
of the locally free
![]() $\mathcal{O}_Y$
-module
$\mathcal{O}_Y$
-module
![]() $\pi _{\ast }\mathcal{O}_{\Sigma _{V,\theta }}$
. We obtain the local section
$\pi _{\ast }\mathcal{O}_{\Sigma _{V,\theta }}$
. We obtain the local section
![]() ${\mathop{\textrm{tr}}\nolimits }(f):={\mathop{\textrm{tr}}\nolimits }(F_f)$
of
${\mathop{\textrm{tr}}\nolimits }(f):={\mathop{\textrm{tr}}\nolimits }(F_f)$
of
![]() $\mathcal{O}_Y$
.
$\mathcal{O}_Y$
.
Let
![]() $C_{L_V}$
be a non-degenerate symmetric pairing of
$C_{L_V}$
be a non-degenerate symmetric pairing of
![]() $L_V$
. We obtain the non-degenerate pairing
$L_V$
. We obtain the non-degenerate pairing
![]() $C$
of
$C$
of
![]() $V=\pi _{\ast }L_V$
:
$V=\pi _{\ast }L_V$
:
Proposition 2.5.
This procedure induces an equivalence between non-degenerate symmetric pairings of
![]() $L_V$
and non-degenerate symmetric pairings of
$L_V$
and non-degenerate symmetric pairings of
![]() $(V,\theta )$
.
$(V,\theta )$
.
We recall the following proposition.
Proposition 2.6 [Reference Li and MochizukiLM10b, Proposition 2.30]. For any non-degenerate symmetric pairing
![]() $C$
of
$C$
of
![]() $(V,\theta )$
, there exists a unique decoupled harmonic metric
$(V,\theta )$
, there exists a unique decoupled harmonic metric
![]() $h^C$
of
$h^C$
of
![]() $(V,\theta )$
which is compatible with
$(V,\theta )$
which is compatible with
![]() $C$
.
$C$
.
Indeed, let
![]() $C_{L_V}$
be the non-degenerate symmetric pairing of
$C_{L_V}$
be the non-degenerate symmetric pairing of
![]() $L_V$
corresponding to
$L_V$
corresponding to
![]() $C$
. Let
$C$
. Let
![]() $h_{L_V}$
be the unique Hermitian metric of
$h_{L_V}$
be the unique Hermitian metric of
![]() $L_V$
satisfying
$L_V$
satisfying
![]() $h_{L_V}(s,s)=|C_{L_V}(s,s)|$
. We obtain the Hermitian metric
$h_{L_V}(s,s)=|C_{L_V}(s,s)|$
. We obtain the Hermitian metric
![]() $h^C$
corresponding to
$h^C$
corresponding to
![]() $h_{L_V}$
. Then,
$h_{L_V}$
. Then,
![]() $h^C$
is the decoupled harmonic metric compatible with
$h^C$
is the decoupled harmonic metric compatible with
![]() $C$
.
$C$
.
As for the converse, the following holds.
Lemma 2.7.
Let
![]() $h$
be a decoupled harmonic metric of
$h$
be a decoupled harmonic metric of
![]() $(V,\theta )$
. There exists a non-degenerate symmetric pairing of
$(V,\theta )$
. There exists a non-degenerate symmetric pairing of
![]() $(V,\theta )$
compatible with
$(V,\theta )$
compatible with
![]() $h$
if and only if the following condition is satisfied.
$h$
if and only if the following condition is satisfied.
-
– Let
 $h_{L_V}$
be the corresponding Hermitian metric of
$h_{L_V}$
be the corresponding Hermitian metric of
 $L_V$
, whose Chern connection is flat. Let
$L_V$
, whose Chern connection is flat. Let
 $\Sigma _{V,\theta, i}$
be any connected component of
$\Sigma _{V,\theta, i}$
be any connected component of
 $\Sigma _{V,\theta }$
. Let
$\Sigma _{V,\theta }$
. Let
 $\rho _i:\pi _1(\Sigma _{V,\theta, i})\to S^1$
be the homomorphism obtained as the monodromy of
$\rho _i:\pi _1(\Sigma _{V,\theta, i})\to S^1$
be the homomorphism obtained as the monodromy of
 $(L_V,h_{L_V})_{|\Sigma _{V,\theta, i}}$
. Then, the image of
$(L_V,h_{L_V})_{|\Sigma _{V,\theta, i}}$
. Then, the image of
 $\rho _i$
is contained in
$\rho _i$
is contained in
 $\{\pm 1\}$
.
$\{\pm 1\}$
.
Proof.
There exists a non-degenerate symmetric pairing of
![]() $(V,\theta )$
compatible with
$(V,\theta )$
compatible with
![]() $h$
if and only if there exists a non-degenerate symmetric pairing
$h$
if and only if there exists a non-degenerate symmetric pairing
![]() $C_{L_V}$
of
$C_{L_V}$
of
![]() $L_V$
compatible with
$L_V$
compatible with
![]() $h_{L_V}$
. If such a
$h_{L_V}$
. If such a
![]() $C_{L_V}$
exists, then each
$C_{L_V}$
exists, then each
![]() $\rho _i$
comes from an
$\rho _i$
comes from an
![]() $\mathbb{R}$
-representation. (See [Reference Li and MochizukiLM10b, §2].) Hence, the image is contained in
$\mathbb{R}$
-representation. (See [Reference Li and MochizukiLM10b, §2].) Hence, the image is contained in
![]() $\{\pm 1\}$
. Conversely, if the image of each
$\{\pm 1\}$
. Conversely, if the image of each
![]() $\rho _i$
is contained in
$\rho _i$
is contained in
![]() $\{\pm 1\}$
, then it is easy to construct such a pairing
$\{\pm 1\}$
, then it is easy to construct such a pairing
![]() $C_{L_V}$
.
$C_{L_V}$
.
2.3 Dirichlet problem for wild harmonic bundles on curves
Let
![]() $Y$
be a Riemann surface equipped with a Kähler metric
$Y$
be a Riemann surface equipped with a Kähler metric
![]() $g_Y$
. Let
$g_Y$
. Let
![]() $X\subset Y$
be a connected relatively compact connected open subset whose boundary
$X\subset Y$
be a connected relatively compact connected open subset whose boundary
![]() ${\partial } X$
is smooth and non-empty. Let
${\partial } X$
is smooth and non-empty. Let
![]() $D\subset X$
be a finite subset.
$D\subset X$
be a finite subset.
Let
![]() $(\mathcal{P}_{\ast }\mathcal{V},\theta )$
be a good filtered Higgs bundle on
$(\mathcal{P}_{\ast }\mathcal{V},\theta )$
be a good filtered Higgs bundle on
![]() $(Y,D)$
of rank
$(Y,D)$
of rank
![]() $r$
. (See [Reference MochizukiMoc21, §2.4] for the notion of good filtered Higgs bundles.) We obtain
$r$
. (See [Reference MochizukiMoc21, §2.4] for the notion of good filtered Higgs bundles.) We obtain
![]() $(\det (\mathcal{P}_{\ast }\mathcal{V}),{\mathop{\textrm{tr}}\nolimits }(\theta ))$
. We set
$(\det (\mathcal{P}_{\ast }\mathcal{V}),{\mathop{\textrm{tr}}\nolimits }(\theta ))$
. We set
![]() $(V,\theta )=(\mathcal{V},\theta )_{|Y\setminus D}$
. Let
$(V,\theta )=(\mathcal{V},\theta )_{|Y\setminus D}$
. Let
![]() $h_{{\partial } X}$
be a Hermitian metric of
$h_{{\partial } X}$
be a Hermitian metric of
![]() $V_{|{\partial } X}$
.
$V_{|{\partial } X}$
.
Theorem 2.8.
There exists a unique harmonic metric
![]() $h$
of
$h$
of
![]() $(V,\overline{\partial }_V,\theta )_{|X\setminus D}$
such that (i)
$(V,\overline{\partial }_V,\theta )_{|X\setminus D}$
such that (i)
![]() $h_{|{\partial } X}=h_{{\partial } X}$
and (ii)
$h_{|{\partial } X}=h_{{\partial } X}$
and (ii)
![]() $\mathcal{P}^h_{\ast }(V)=\mathcal{P}_{\ast }\mathcal{V}$
. (See [Reference MochizukiMoc21
, §2.5] for the filtered sheaf
$\mathcal{P}^h_{\ast }(V)=\mathcal{P}_{\ast }\mathcal{V}$
. (See [Reference MochizukiMoc21
, §2.5] for the filtered sheaf
![]() $\mathcal{P}^h_{\ast }(V)$
.)
$\mathcal{P}^h_{\ast }(V)$
.)
Proof.
Let us study the case
![]() $r=1$
. There exists a Hermitian metric
$r=1$
. There exists a Hermitian metric
![]() $h_0$
of
$h_0$
of
![]() $V$
such that (i)
$V$
such that (i)
![]() $h_{0|{\partial } X}=h_{{\partial } X}$
, (ii)
$h_{0|{\partial } X}=h_{{\partial } X}$
, (ii)
![]() $h_0$
is flat around any point of
$h_0$
is flat around any point of
![]() $D$
, and (iii)
$D$
, and (iii)
![]() $\mathcal{P}^{h_0}_{\ast }(V)=\mathcal{P}_{\ast }V$
. There exists a
$\mathcal{P}^{h_0}_{\ast }(V)=\mathcal{P}_{\ast }V$
. There exists a
![]() $C^{\infty }$
-function
$C^{\infty }$
-function
![]() $\alpha :X\to \mathbb{R}$
such that
$\alpha :X\to \mathbb{R}$
such that
![]() $\alpha _{|{\partial } X}=0$
and that
$\alpha _{|{\partial } X}=0$
and that
![]() $\overline{\partial }{\partial }\alpha =R(h_0)$
. Then,
$\overline{\partial }{\partial }\alpha =R(h_0)$
. Then,
![]() $h=e^{-\alpha }h_0$
is a flat metric of
$h=e^{-\alpha }h_0$
is a flat metric of
![]() $V$
satisfying the desired conditions. Let
$V$
satisfying the desired conditions. Let
![]() $h'$
be another flat metric satisfying the same condition. We obtain the
$h'$
be another flat metric satisfying the same condition. We obtain the
![]() $C^{\infty }$
-function
$C^{\infty }$
-function
![]() $s$
on
$s$
on
![]() $X$
determined by
$X$
determined by
![]() $h'=e^sh$
. Because
$h'=e^sh$
. Because
![]() $\Delta _{g_Y}s=0$
and
$\Delta _{g_Y}s=0$
and
![]() $s_{|{\partial } X}=0$
, we obtain that
$s_{|{\partial } X}=0$
, we obtain that
![]() $s=0$
on
$s=0$
on
![]() $X$
, and hence
$X$
, and hence
![]() $h'=h$
.
$h'=h$
.
Let us study the case
![]() $r\geqslant 2$
. At each point
$r\geqslant 2$
. At each point
![]() $P\in D$
, let
$P\in D$
, let
![]() $(X_P,z_P)$
be a holomorphic coordinate neighbourhood around
$(X_P,z_P)$
be a holomorphic coordinate neighbourhood around
![]() $P$
such that (i)
$P$
such that (i)
![]() $X_P$
is relatively compact in
$X_P$
is relatively compact in
![]() $X\setminus (D\setminus \{P\})$
, (ii)
$X\setminus (D\setminus \{P\})$
, (ii)
![]() $\overline{X}_{P}\cap \overline{X}_{P'}=\emptyset$
for any
$\overline{X}_{P}\cap \overline{X}_{P'}=\emptyset$
for any
![]() $P,P'\in D$
, and (iii) the coordinate
$P,P'\in D$
, and (iii) the coordinate
![]() $z_P$
induces
$z_P$
induces
![]() $(X_P,P)\simeq (\{|z|\lt 1\},0)$
. Let
$(X_P,P)\simeq (\{|z|\lt 1\},0)$
. Let
![]() $h_{\det (V)}$
be a flat metric of
$h_{\det (V)}$
be a flat metric of
![]() $\det (V)$
adapted to
$\det (V)$
adapted to
![]() $\det (\mathcal{P}_{\ast }V)$
such that
$\det (\mathcal{P}_{\ast }V)$
such that
![]() $h_{\det (V)|{\partial } X}=\det (h_{{\partial } X})$
. Let
$h_{\det (V)|{\partial } X}=\det (h_{{\partial } X})$
. Let
![]() $h_0$
be a Hermitian metric of
$h_0$
be a Hermitian metric of
![]() $V$
such that (i)
$V$
such that (i)
![]() $h_{0|{\partial } X}=h_{{\partial } X}$
, (ii)
$h_{0|{\partial } X}=h_{{\partial } X}$
, (ii)
![]() $\det (h_0)=h_{\det (V)}$
, (iii)
$\det (h_0)=h_{\det (V)}$
, (iii)
![]() $\mathcal{P}^{h_0}_{\ast }(V)=\mathcal{P}_{\ast }\mathcal{V}$
, and (iv) around
$\mathcal{P}^{h_0}_{\ast }(V)=\mathcal{P}_{\ast }\mathcal{V}$
, and (iv) around
![]() $P\in D$
, we have
$P\in D$
, we have
![]() $\bigl | R(h_0)+[\theta, \theta ^{\dagger }_{h_0}] \bigr |_{h,g_Y} =O(|z_P|^{-2+\epsilon })$
for some
$\bigl | R(h_0)+[\theta, \theta ^{\dagger }_{h_0}] \bigr |_{h,g_Y} =O(|z_P|^{-2+\epsilon })$
for some
![]() $\epsilon \gt 0$
. (For example, see [Reference MochizukiMoc21] for the construction.) We set
$\epsilon \gt 0$
. (For example, see [Reference MochizukiMoc21] for the construction.) We set
![]() $F(h_0)=R(h_0)+[\theta, \theta ^{\dagger }_{h_0}]$
. There exists
$F(h_0)=R(h_0)+[\theta, \theta ^{\dagger }_{h_0}]$
. There exists
![]() $p\gt 1$
such that
$p\gt 1$
such that
![]() $F(h_0)$
is
$F(h_0)$
is
![]() $L^p$
on
$L^p$
on
![]() $X$
. There exists an
$X$
. There exists an
![]() $L_2^p$
-function
$L_2^p$
-function
![]() $\alpha$
on
$\alpha$
on
![]() $X$
such that (i)
$X$
such that (i)
![]() $\Delta _{g_Y}(\alpha )=|F(h_0)_{|X}|_{h_0,g_Y}$
and (ii)
$\Delta _{g_Y}(\alpha )=|F(h_0)_{|X}|_{h_0,g_Y}$
and (ii)
![]() $\alpha _{|{\partial } X}=0$
. There exists
$\alpha _{|{\partial } X}=0$
. There exists
![]() $C_0\gt 0$
such that
$C_0\gt 0$
such that
![]() $|\alpha |\lt C_0$
on
$|\alpha |\lt C_0$
on
![]() $X$
.
$X$
.
For
![]() $0\lt \delta \lt 1$
, we set
$0\lt \delta \lt 1$
, we set
![]() $X_P(\delta )=\{|z_P|\lt \delta \}$
and
$X_P(\delta )=\{|z_P|\lt \delta \}$
and
![]() $Z(\delta ):=X\setminus \bigcup _{P\in D}X_P(\delta )$
. We have
$Z(\delta ):=X\setminus \bigcup _{P\in D}X_P(\delta )$
. We have
![]() ${\partial } Z(\delta )={\partial } X\cup \bigcup _{P\in D}{\partial } X_P(\delta )$
. By the Dirichlet problem for harmonic metrics [Reference DonaldsonDon92, Reference Li and MochizukiLM10a], there exists a harmonic metric
${\partial } Z(\delta )={\partial } X\cup \bigcup _{P\in D}{\partial } X_P(\delta )$
. By the Dirichlet problem for harmonic metrics [Reference DonaldsonDon92, Reference Li and MochizukiLM10a], there exists a harmonic metric
![]() $h_{Z(\delta )}$
of
$h_{Z(\delta )}$
of
![]() $(V,\overline{\partial }_V,\theta )_{|Z(\delta )}$
such that (i)
$(V,\overline{\partial }_V,\theta )_{|Z(\delta )}$
such that (i)
![]() $\det (h_{Z(\delta )})=h_{\det (V)|Z(\delta )}$
and (ii)
$\det (h_{Z(\delta )})=h_{\det (V)|Z(\delta )}$
and (ii)
![]() $h_{Z(\delta )|{\partial } Z(\delta )}=h_{0|{\partial } Z(\delta )}$
. Let
$h_{Z(\delta )|{\partial } Z(\delta )}=h_{0|{\partial } Z(\delta )}$
. Let
![]() $s_{Z(\delta )}$
be the automorphism of
$s_{Z(\delta )}$
be the automorphism of
![]() $V_{|Z(\delta )}$
determined by
$V_{|Z(\delta )}$
determined by
![]() $h_{Z(\delta )}=h_{0|Z(\delta )}\cdot s_{Z(\delta )}$
. According to [Reference SimpsonSim88, Lemma 3.1], the following holds on
$h_{Z(\delta )}=h_{0|Z(\delta )}\cdot s_{Z(\delta )}$
. According to [Reference SimpsonSim88, Lemma 3.1], the following holds on
![]() $Z(\delta )$
:
$Z(\delta )$
:
Because
![]() $\Delta _{g_Y}\bigl ( \log{\mathop{\textrm{Tr}}\nolimits }(s_{Z(\delta )})-\alpha \bigr ) \leqslant 0$
, we obtain
$\Delta _{g_Y}\bigl ( \log{\mathop{\textrm{Tr}}\nolimits }(s_{Z(\delta )})-\alpha \bigr ) \leqslant 0$
, we obtain
Because
![]() $\det (s_{Z(\delta )})=1$
, there exists
$\det (s_{Z(\delta )})=1$
, there exists
![]() $C_1\gt 0$
, which depends only on
$C_1\gt 0$
, which depends only on
![]() $C_0$
and
$C_0$
and
![]() $r$
, such that
$r$
, such that
Then, there exists a sequence
![]() $\delta (i)\to 0$
$\delta (i)\to 0$
![]() $(i=1,2,\ldots)$
such that the following hold (see [Reference Li and MochizukiLM10a, Proposition 2.6]).
$(i=1,2,\ldots)$
such that the following hold (see [Reference Li and MochizukiLM10a, Proposition 2.6]).
-
– The sequence
 $h_{Z(\delta (i))}$
is convergent in the
$h_{Z(\delta (i))}$
is convergent in the
 $C^{\infty }$
-sense on any relatively compact open subset of
$C^{\infty }$
-sense on any relatively compact open subset of
 $X\setminus D$
. Let
$X\setminus D$
. Let
 $h_{\infty }$
denote the limit, which is a harmonic metric.
$h_{\infty }$
denote the limit, which is a harmonic metric. -
–
 $h_{\infty }$
is mutually bounded with
$h_{\infty }$
is mutually bounded with
 $h_0$
. As a result,
$h_0$
. As a result,
 $\mathcal{P}^{h_{\infty }}_{\ast }(V)=\mathcal{P}_{\ast }\mathcal{V}_{|X}$
.
$\mathcal{P}^{h_{\infty }}_{\ast }(V)=\mathcal{P}_{\ast }\mathcal{V}_{|X}$
. -
–
 $\det (h_{\infty })=h_{\det (V)}$
.
$\det (h_{\infty })=h_{\det (V)}$
.
Let
![]() $Z:=Z(1/2)$
. There exists a harmonic metric
$Z:=Z(1/2)$
. There exists a harmonic metric
![]() $h_{1,Z}$
of
$h_{1,Z}$
of
![]() $(V,\overline{\partial }_V,\theta )_{|Z}$
such that (i)
$(V,\overline{\partial }_V,\theta )_{|Z}$
such that (i)
![]() $\det (h_{1,Z})=h_{\det (V)|Z}$
, (ii)
$\det (h_{1,Z})=h_{\det (V)|Z}$
, (ii)
![]() $h_{1,Z|{\partial } X_P(1/2)}=h_{\infty |{\partial } X_P(1/2)}$
for any
$h_{1,Z|{\partial } X_P(1/2)}=h_{\infty |{\partial } X_P(1/2)}$
for any
![]() $P\in D$
, and (iii)
$P\in D$
, and (iii)
![]() $h_{1,Z|{\partial } X}=h_{0|{\partial } X}$
. Let
$h_{1,Z|{\partial } X}=h_{0|{\partial } X}$
. Let
![]() $i_0$
such that
$i_0$
such that
![]() $\delta (i_0)\lt 1/2$
. Let
$\delta (i_0)\lt 1/2$
. Let
![]() $s_{1,\delta (i)}$
be the automorphism of
$s_{1,\delta (i)}$
be the automorphism of
![]() $V_{|Z}$
determined by
$V_{|Z}$
determined by
![]() $h_{Z(\delta (i))|Z}=h_{1,Z}\cdot s_{1,\delta (i)}$
. We obtain
$h_{Z(\delta (i))|Z}=h_{1,Z}\cdot s_{1,\delta (i)}$
. We obtain
![]() $\Delta _{g_Y}\log{\mathop{\textrm{Tr}}\nolimits }(s_{1,\delta (i)})\leqslant 0$
on
$\Delta _{g_Y}\log{\mathop{\textrm{Tr}}\nolimits }(s_{1,\delta (i)})\leqslant 0$
on
![]() $Z$
. Hence, we obtain
$Z$
. Hence, we obtain
Because
![]() $\log{\mathop{\textrm{Tr}}\nolimits }(s_{1,\delta (i)}/r)\to 0$
on
$\log{\mathop{\textrm{Tr}}\nolimits }(s_{1,\delta (i)}/r)\to 0$
on
![]() $\bigcup _{P\in D}{\partial } X_P(1/2)$
, we obtain that
$\bigcup _{P\in D}{\partial } X_P(1/2)$
, we obtain that
![]() $s_{1,\delta (i)}\to{\mathop{\textrm{id}}\nolimits }_{V}$
on
$s_{1,\delta (i)}\to{\mathop{\textrm{id}}\nolimits }_{V}$
on
![]() $Z$
. Hence, we obtain
$Z$
. Hence, we obtain
![]() $h_{\infty |Z}=h_{1,Z}$
, which implies that
$h_{\infty |Z}=h_{1,Z}$
, which implies that
![]() $h_{\infty }$
satisfies the condition
$h_{\infty }$
satisfies the condition
![]() $h_{\infty |{\partial } X}=h_{0|{\partial } X}$
.
$h_{\infty |{\partial } X}=h_{0|{\partial } X}$
.
Let
![]() $h'$
be another harmonic metric satisfying the conditions (i) and (ii). Note that
$h'$
be another harmonic metric satisfying the conditions (i) and (ii). Note that
![]() $\det (h')=h_{\det (V)}$
. Let
$\det (h')=h_{\det (V)}$
. Let
![]() $s$
be the automorphism of
$s$
be the automorphism of
![]() $V$
determined by
$V$
determined by
![]() $h'=h\cdot s$
. By [Reference SimpsonSim88, Lemma 3.1], we have the following equality on
$h'=h\cdot s$
. By [Reference SimpsonSim88, Lemma 3.1], we have the following equality on
![]() $X\setminus D$
:
$X\setminus D$
:
This implies that
![]() ${\mathop{\textrm{Tr}}\nolimits }(s)$
is subharmonic on
${\mathop{\textrm{Tr}}\nolimits }(s)$
is subharmonic on
![]() $X\setminus D$
. Because
$X\setminus D$
. Because
![]() ${\mathop{\textrm{Tr}}\nolimits }(s)$
is bounded, we obtain that
${\mathop{\textrm{Tr}}\nolimits }(s)$
is bounded, we obtain that
![]() ${\mathop{\textrm{Tr}}\nolimits }(s)$
is a subharmonic function on
${\mathop{\textrm{Tr}}\nolimits }(s)$
is a subharmonic function on
![]() $X$
(see [Reference SimpsonSim90, Lemma 2.2]). We obtain
$X$
(see [Reference SimpsonSim90, Lemma 2.2]). We obtain
![]() $\max _X{\mathop{\textrm{Tr}}\nolimits }(s)\leqslant \max _{{\partial } X}{\mathop{\textrm{Tr}}\nolimits }(s)=r$
. Because
$\max _X{\mathop{\textrm{Tr}}\nolimits }(s)\leqslant \max _{{\partial } X}{\mathop{\textrm{Tr}}\nolimits }(s)=r$
. Because
![]() $\det (s)=1$
, we have
$\det (s)=1$
, we have
![]() ${\mathop{\textrm{Tr}}\nolimits }(s)\geqslant r$
. Hence, we obtain
${\mathop{\textrm{Tr}}\nolimits }(s)\geqslant r$
. Hence, we obtain
![]() ${\mathop{\textrm{Tr}}\nolimits }(s)=r$
on
${\mathop{\textrm{Tr}}\nolimits }(s)=r$
on
![]() $X$
, which implies
$X$
, which implies
![]() $s={\mathop{\textrm{id}}\nolimits }_V$
.
$s={\mathop{\textrm{id}}\nolimits }_V$
.
Corollary 2.9.
Suppose that
![]() $(\mathcal{P}_{\ast }\mathcal{V},\theta )$
is equipped with a perfect symmetric pairing
$(\mathcal{P}_{\ast }\mathcal{V},\theta )$
is equipped with a perfect symmetric pairing
![]() $C$
. If
$C$
. If
![]() $h_{{\partial } X}$
is compatible with
$h_{{\partial } X}$
is compatible with
![]() $C_{|{\partial } X}$
, then
$C_{|{\partial } X}$
, then
![]() $h$
is also compatible with
$h$
is also compatible with
![]() $C$
.
$C$
.
Proof.
Let
![]() $h_{{\partial } X}^{\lor }$
be the Hermitian metric of
$h_{{\partial } X}^{\lor }$
be the Hermitian metric of
![]() $V^{\lor }_{|{\partial } X}$
induced by
$V^{\lor }_{|{\partial } X}$
induced by
![]() $h_{{\partial } X}$
. Let
$h_{{\partial } X}$
. Let
![]() $h^{\lor }$
be the Hermitian metric of
$h^{\lor }$
be the Hermitian metric of
![]() $V^{\lor }$
induced by
$V^{\lor }$
induced by
![]() $h$
. Then,
$h$
. Then,
![]() $h^{\lor }$
is the unique harmonic metric of
$h^{\lor }$
is the unique harmonic metric of
![]() $(V^{\lor },\theta ^{\lor })$
satisfying
$(V^{\lor },\theta ^{\lor })$
satisfying
![]() $h^{\lor }_{|{\partial } X}=h_{{\partial } X}^{\lor }$
.
$h^{\lor }_{|{\partial } X}=h_{{\partial } X}^{\lor }$
.
Let
![]() $\Psi _C:(V,\theta )\simeq (V^{\lor },\theta ^{\lor })$
denote the isomorphism induced by
$\Psi _C:(V,\theta )\simeq (V^{\lor },\theta ^{\lor })$
denote the isomorphism induced by
![]() $C$
. Because
$C$
. Because
![]() $h_{{\partial } X}$
is compatible with
$h_{{\partial } X}$
is compatible with
![]() $C$
,
$C$
,
![]() $h_{{\partial } X}=\Psi _C^{\ast }h_{{\partial } X}^{\lor }$
holds on
$h_{{\partial } X}=\Psi _C^{\ast }h_{{\partial } X}^{\lor }$
holds on
![]() ${\partial } X$
. By the uniqueness, we obtain
${\partial } X$
. By the uniqueness, we obtain
![]() $h=\Psi _C^{\ast }(h^{\lor })$
, i.e.
$h=\Psi _C^{\ast }(h^{\lor })$
, i.e.
![]() $h$
is compatible with
$h$
is compatible with
![]() $C$
.
$C$
.
3. Large-scale solutions in the symmetric case
3.1 Preliminary from linear algebra
3.1.1 Hermitian metrics compatible with a non-degenerate symmetric pairing
Let
![]() $V$
be an
$V$
be an
![]() $r$
-dimensional
$r$
-dimensional
![]() $\mathbb{C}$
-vector space. The dual space is denoted by
$\mathbb{C}$
-vector space. The dual space is denoted by
![]() $V^{\lor }$
. An
$V^{\lor }$
. An
![]() $\mathbb{R}$
-structure of
$\mathbb{R}$
-structure of
![]() $V$
is an
$V$
is an
![]() $r$
-dimensional
$r$
-dimensional
![]() $\mathbb{R}$
-subspace
$\mathbb{R}$
-subspace
![]() $V_{\mathbb{R}}$
such that the natural morphism
$V_{\mathbb{R}}$
such that the natural morphism
![]() $\mathbb{C}\otimes _{\mathbb{R}}V_{\mathbb{R}}\longrightarrow V$
is an isomorphism. A positive definite symmetric bilinear form
$\mathbb{C}\otimes _{\mathbb{R}}V_{\mathbb{R}}\longrightarrow V$
is an isomorphism. A positive definite symmetric bilinear form
![]() $C_{\mathbb{R}}$
of
$C_{\mathbb{R}}$
of
![]() $V_{\mathbb{R}}$
induces a Hermitian metric
$V_{\mathbb{R}}$
induces a Hermitian metric
![]() $h$
and a non-degenerate symmetric bilinear form
$h$
and a non-degenerate symmetric bilinear form
![]() $C$
of
$C$
of
![]() $V$
by
$V$
by
![]() $h(\alpha \otimes u,\beta \otimes v) =\alpha \overline{\beta } C_{\mathbb{R}}(u,v)$
and
$h(\alpha \otimes u,\beta \otimes v) =\alpha \overline{\beta } C_{\mathbb{R}}(u,v)$
and
![]() $C(\alpha \otimes u,\beta \otimes v) =\alpha \beta C_{\mathbb{R}}(u,v)$
for any
$C(\alpha \otimes u,\beta \otimes v) =\alpha \beta C_{\mathbb{R}}(u,v)$
for any
![]() $\alpha, \beta \in \mathbb{C}$
and
$\alpha, \beta \in \mathbb{C}$
and
![]() $u,v\in V_{\mathbb{R}}$
. An orthogonal decomposition
$u,v\in V_{\mathbb{R}}$
. An orthogonal decomposition
![]() $V_{\mathbb{R}}=\bigoplus V_{\mathbb{R},i}$
with respect to
$V_{\mathbb{R}}=\bigoplus V_{\mathbb{R},i}$
with respect to
![]() $C_{\mathbb{R}}$
induces a decomposition
$C_{\mathbb{R}}$
induces a decomposition
![]() $V=\bigoplus V_{\mathbb{R},i}\otimes \mathbb{C}$
which is clearly orthogonal with respect to both
$V=\bigoplus V_{\mathbb{R},i}\otimes \mathbb{C}$
which is clearly orthogonal with respect to both
![]() $h$
and
$h$
and
![]() $C$
.
$C$
.
Let
![]() $C$
be a non-degenerate symmetric pairing of
$C$
be a non-degenerate symmetric pairing of
![]() $V$
. It induces a
$V$
. It induces a
![]() $\mathbb{C}$
-linear morphism
$\mathbb{C}$
-linear morphism
![]() $\Psi _C:V\to V^{\lor }$
. A Hermitian metric
$\Psi _C:V\to V^{\lor }$
. A Hermitian metric
![]() $h$
of
$h$
of
![]() $V$
is called compatible with
$V$
is called compatible with
![]() $C$
if
$C$
if
![]() $\Psi _C$
is isometry between
$\Psi _C$
is isometry between
![]() $(V,h)$
and
$(V,h)$
and
![]() $(V^{\lor },h^{\lor })$
, where
$(V^{\lor },h^{\lor })$
, where
![]() $h^{\lor }$
denotes the Hermitian metric of
$h^{\lor }$
denotes the Hermitian metric of
![]() $V^{\lor }$
induced by
$V^{\lor }$
induced by
![]() $h$
. If
$h$
. If
![]() $h$
is compatible with
$h$
is compatible with
![]() $C$
, there uniquely exists an
$C$
, there uniquely exists an
![]() $\mathbb{R}$
-structure
$\mathbb{R}$
-structure
![]() $V_{\mathbb{R}}$
of
$V_{\mathbb{R}}$
of
![]() $V$
equipped with a positive definite symmetric bilinear form
$V$
equipped with a positive definite symmetric bilinear form
![]() $C_{\mathbb{R}}$
such that (i)
$C_{\mathbb{R}}$
such that (i)
![]() $V_{\mathbb{R}}\otimes \mathbb{C}=V$
and (ii)
$V_{\mathbb{R}}\otimes \mathbb{C}=V$
and (ii)
![]() $h$
and
$h$
and
![]() $C$
are induced by
$C$
are induced by
![]() $C_{\mathbb{R}}$
.
$C_{\mathbb{R}}$
.
3.1.2 An estimate
Let
![]() $C$
be a non-degenerate symmetric form of
$C$
be a non-degenerate symmetric form of
![]() $V$
. Let
$V$
. Let
![]() $V=\bigoplus _{i=1}^r V_i$
be an orthogonal decomposition with respect to
$V=\bigoplus _{i=1}^r V_i$
be an orthogonal decomposition with respect to
![]() $C$
such that
$C$
such that
![]() $\dim V_i=1$
. The following lemma is obvious.
$\dim V_i=1$
. The following lemma is obvious.
Lemma 3.1.
There exists a unique Hermitian metric
![]() $h_0$
of
$h_0$
of
![]() $V$
such that (i)
$V$
such that (i)
![]() $h_0$
is compatible with
$h_0$
is compatible with
![]() $C$
and (ii) the decomposition
$C$
and (ii) the decomposition
![]() $V=\bigoplus V_i$
is orthogonal with respect to
$V=\bigoplus V_i$
is orthogonal with respect to
![]() $h_0$
.
$h_0$
.
For any Hermitian metric
![]() $h$
of
$h$
of
![]() $V$
compatible with
$V$
compatible with
![]() $C$
, let
$C$
, let
![]() $s(h_0,h)$
be the automorphism of
$s(h_0,h)$
be the automorphism of
![]() $V$
determined by the condition
$V$
determined by the condition
![]() $h(u,v)=h_0(s(h_0,h)u,v)$
for any
$h(u,v)=h_0(s(h_0,h)u,v)$
for any
![]() $u,v\in V$
. Note that
$u,v\in V$
. Note that
![]() $\det (s(h_0,h))=1$
. Let
$\det (s(h_0,h))=1$
. Let
![]() $\mathcal{H}(C;\epsilon )$
be the set of Hermitian metrics
$\mathcal{H}(C;\epsilon )$
be the set of Hermitian metrics
![]() $h$
of
$h$
of
![]() $V$
compatible with
$V$
compatible with
![]() $C$
such that the following holds for any
$C$
such that the following holds for any
![]() $u\in V_i$
,
$u\in V_i$
,
![]() $v\in V_j$
$v\in V_j$
![]() $(i\neq j)$
:
$(i\neq j)$
:
Lemma 3.2.
There exists
![]() $C\gt 0$
, depending only on
$C\gt 0$
, depending only on
![]() $r$
, such that the following holds for any
$r$
, such that the following holds for any
![]() $0\leqslant \epsilon \leqslant (2r)^{-1}$
and any
$0\leqslant \epsilon \leqslant (2r)^{-1}$
and any
![]() $h\in \mathcal{H}(C;\epsilon )$
:
$h\in \mathcal{H}(C;\epsilon )$
:
Proof.
Let
![]() $e_i$
be a base of
$e_i$
be a base of
![]() $V_i$
such that
$V_i$
such that
![]() $C(e_i,e_i)=1$
. Note that the tuple
$C(e_i,e_i)=1$
. Note that the tuple
![]() $(e_1,\ldots, e_r)$
is an orthonormal base with respect to
$(e_1,\ldots, e_r)$
is an orthonormal base with respect to
![]() $h_0$
. Let
$h_0$
. Let
![]() $H$
be the matrix determined by
$H$
be the matrix determined by
![]() $H_{i,j}=h(e_i,e_j)$
. Then, the linear map
$H_{i,j}=h(e_i,e_j)$
. Then, the linear map
![]() $s(h_0,h)$
is represented by the matrix
$s(h_0,h)$
is represented by the matrix
![]() ${}^{t}\!H$
with respect to the base
${}^{t}\!H$
with respect to the base
![]() $(e_1,\ldots, e_r)$
. Because
$(e_1,\ldots, e_r)$
. Because
![]() $h$
is compatible with
$h$
is compatible with
![]() $C$
,
$C$
,
![]() ${}^{t}\!H\cdot H$
is the identity matrix. We obtain
${}^{t}\!H\cdot H$
is the identity matrix. We obtain
 \begin{align} H_{i,i}^2-1 =-\sum _{\substack{1\leqslant j\leqslant r \\[5pt] j\neq i}}H_{i,j}H_{j,i}. \end{align}
\begin{align} H_{i,i}^2-1 =-\sum _{\substack{1\leqslant j\leqslant r \\[5pt] j\neq i}}H_{i,j}H_{j,i}. \end{align}
By condition (4), we have
![]() $|H_{i,j}| \leqslant \epsilon H_{i,i}^{1/2}H_{j,j}^{1/2}$
for
$|H_{i,j}| \leqslant \epsilon H_{i,i}^{1/2}H_{j,j}^{1/2}$
for
![]() $i\neq j$
. We obtain
$i\neq j$
. We obtain
 \begin{align*} H_{i,i}^2-1 \leqslant \epsilon \sum _{\substack {1\leqslant j\leqslant r \\[5pt] j\neq i}}H_{i,i}H_{j,j}. \end{align*}
\begin{align*} H_{i,i}^2-1 \leqslant \epsilon \sum _{\substack {1\leqslant j\leqslant r \\[5pt] j\neq i}}H_{i,i}H_{j,j}. \end{align*}
We set
![]() $A=\sum _{j=1}^r H_{j,j}$
. We obtain
$A=\sum _{j=1}^r H_{j,j}$
. We obtain
Lemma 3.3. The following holds:
![]() $H_{i,i}\leqslant \epsilon A+1$
.
$H_{i,i}\leqslant \epsilon A+1$
.
Proof.
Let
![]() $a\gt 0$
. Let us consider the
$a\gt 0$
. Let us consider the
![]() $\mathbb{R}$
-valued function
$\mathbb{R}$
-valued function
![]() $f(s)=s^2-as-1$
$f(s)=s^2-as-1$
![]() $(s\in \mathbb{R})$
. We set
$(s\in \mathbb{R})$
. We set
![]() $s_{\pm }=2^{-1}(a\pm \sqrt{a^2+4})$
, and then we have
$s_{\pm }=2^{-1}(a\pm \sqrt{a^2+4})$
, and then we have
![]() $f(s_{\pm })=0$
and
$f(s_{\pm })=0$
and
![]() $s_-\lt s_+$
. We obtain
$s_-\lt s_+$
. We obtain
![]() $f(s)\gt 0$
for any
$f(s)\gt 0$
for any
![]() $s\gt s_+$
. Hence, if
$s\gt s_+$
. Hence, if
![]() $f(s)\leqslant 0$
, we obtain
$f(s)\leqslant 0$
, we obtain
By setting
![]() $a=\epsilon A$
, we obtain the claim of the lemma from (6) and (7).
$a=\epsilon A$
, we obtain the claim of the lemma from (6) and (7).
We obtain
![]() $A\leqslant \epsilon r A+r$
, and hence
$A\leqslant \epsilon r A+r$
, and hence
![]() $A\leqslant (1-\epsilon r)^{-1}r\leqslant 2r$
. By (4) and (5), we obtain
$A\leqslant (1-\epsilon r)^{-1}r\leqslant 2r$
. By (4) and (5), we obtain
 \begin{align*} |H_{i,i}^2-1| \leqslant \sum _{\substack {1\leqslant j\leqslant r\\[5pt] j\neq i}} |H_{i,j}|\cdot |H_{j,i}| \leqslant \epsilon \sum _{1\leqslant j\leqslant r} H_{i,i}\cdot H_{j,j} \leqslant \epsilon A^2\leqslant 4r^2\epsilon . \end{align*}
\begin{align*} |H_{i,i}^2-1| \leqslant \sum _{\substack {1\leqslant j\leqslant r\\[5pt] j\neq i}} |H_{i,j}|\cdot |H_{j,i}| \leqslant \epsilon \sum _{1\leqslant j\leqslant r} H_{i,i}\cdot H_{j,j} \leqslant \epsilon A^2\leqslant 4r^2\epsilon . \end{align*}
Because
![]() $H_{i,i}$
are positive numbers, we obtain
$H_{i,i}$
are positive numbers, we obtain
![]() $\bigl |H_{i,i}-1\bigr |\leqslant 4r^2\epsilon$
. We also obtain
$\bigl |H_{i,i}-1\bigr |\leqslant 4r^2\epsilon$
. We also obtain
![]() $|H_{i,j}|\leqslant \epsilon (1+4r^2\epsilon )$
.
$|H_{i,j}|\leqslant \epsilon (1+4r^2\epsilon )$
.
3.2 Harmonic metrics compatible with a non-degenerate symmetric pairing
Let
![]() $Y$
be any Riemann surface. Let
$Y$
be any Riemann surface. Let
![]() $(V,\overline{\partial }_V,\theta )$
be a Higgs bundle on
$(V,\overline{\partial }_V,\theta )$
be a Higgs bundle on
![]() $Y$
of rank
$Y$
of rank
![]() $r$
, which is regular semisimple. Let
$r$
, which is regular semisimple. Let
![]() $C$
be a non-degenerate symmetric pairing of
$C$
be a non-degenerate symmetric pairing of
![]() $(V,\theta )$
.
$(V,\theta )$
.
For any
![]() $t\gt 0$
, let
$t\gt 0$
, let
![]() $\mathop{\textrm{Harm}}\nolimits (V,\overline{\partial }_V,t\theta, C)$
denote the set of harmonic metrics of
$\mathop{\textrm{Harm}}\nolimits (V,\overline{\partial }_V,t\theta, C)$
denote the set of harmonic metrics of
![]() $(V,\overline{\partial }_V,t\theta )$
compatible with
$(V,\overline{\partial }_V,t\theta )$
compatible with
![]() $C$
. Let
$C$
. Let
![]() $g_Y$
be a Kähler metric of
$g_Y$
be a Kähler metric of
![]() $Y$
. For any non-negative integer
$Y$
. For any non-negative integer
![]() $\ell$
and
$\ell$
and
![]() $p\gt 1$
, and for any relatively compact open subset
$p\gt 1$
, and for any relatively compact open subset
![]() $K$
of
$K$
of
![]() $Y$
, we define the
$Y$
, we define the
![]() $L_{\ell }^p$
-norm
$L_{\ell }^p$
-norm
![]() $\|f\|_{L_{\ell }^p,K}$
of a section
$\|f\|_{L_{\ell }^p,K}$
of a section
![]() $f$
of
$f$
of
![]() ${\mathop{\textrm{End}}\nolimits }(V)$
on
${\mathop{\textrm{End}}\nolimits }(V)$
on
![]() $K$
by using
$K$
by using
![]() $g_Y$
,
$g_Y$
,
![]() $h^C$
and the Chern connection of
$h^C$
and the Chern connection of
![]() $h^C$
. (See Proposition 2.6 for
$h^C$
. (See Proposition 2.6 for
![]() $h^C$
.)
$h^C$
.)
Theorem 3.4.
Let
![]() $K$
be any relatively compact open subset of
$K$
be any relatively compact open subset of
![]() $Y$
. There exists
$Y$
. There exists
![]() $t(K)\gt 0$
such that:
$t(K)\gt 0$
such that:
-
– for any
 $(\ell, p)\in \mathbb{Z}_{\gt 0}\times \mathbb{R}_{\gt 1}$
, there exist
$(\ell, p)\in \mathbb{Z}_{\gt 0}\times \mathbb{R}_{\gt 1}$
, there exist
 $A(\ell, p,K)\gt 0$
and
$A(\ell, p,K)\gt 0$
and
 $\epsilon (\ell, p,K)\gt 0$
such that, for any
$\epsilon (\ell, p,K)\gt 0$
such that, for any
 $h\in \mathop{\textrm{Harm}}\nolimits (V,\overline{\partial }_V,t\theta, C)$
$h\in \mathop{\textrm{Harm}}\nolimits (V,\overline{\partial }_V,t\theta, C)$
 $(t\geqslant t(K))$
,(8)
$(t\geqslant t(K))$
,(8) \begin{align} \bigl \| s(h^C,h)-{\mathop{\textrm{id}}\nolimits }_E \bigr \|_{L_{\ell }^p,K} + \bigl \| s(h^C,h)^{-1}-{\mathop{\textrm{id}}\nolimits }_E \bigr \|_{L_{\ell }^p,K} \leqslant A(\ell, p,K)\exp (-\epsilon (\ell, p,K)t). \end{align}
\begin{align} \bigl \| s(h^C,h)-{\mathop{\textrm{id}}\nolimits }_E \bigr \|_{L_{\ell }^p,K} + \bigl \| s(h^C,h)^{-1}-{\mathop{\textrm{id}}\nolimits }_E \bigr \|_{L_{\ell }^p,K} \leqslant A(\ell, p,K)\exp (-\epsilon (\ell, p,K)t). \end{align}
Proof.
To simplify the description, we set
![]() $s(h):=s(h^C,h)$
in this proof. By [Reference MochizukiMoc16, Corollary 2.6] and Lemma 3.2, there exist
$s(h):=s(h^C,h)$
in this proof. By [Reference MochizukiMoc16, Corollary 2.6] and Lemma 3.2, there exist
![]() $A(K)\gt 0$
,
$A(K)\gt 0$
,
![]() $\epsilon (K)\gt 0$
, and
$\epsilon (K)\gt 0$
, and
![]() $t(K)\gt 0$
such that the following holds for any
$t(K)\gt 0$
such that the following holds for any
![]() $h\in \mathop{\textrm{Harm}}\nolimits (V,\overline{\partial }_V,t\theta, C)$
$h\in \mathop{\textrm{Harm}}\nolimits (V,\overline{\partial }_V,t\theta, C)$
![]() $(t\geqslant t(K))$
:
$(t\geqslant t(K))$
:
Let
![]() $R(h)$
denote the curvature of the Chern connection of
$R(h)$
denote the curvature of the Chern connection of
![]() $(V,\overline{\partial }_V,h)$
. By [Reference MochizukiMoc16, Theorem 2.9], there exist
$(V,\overline{\partial }_V,h)$
. By [Reference MochizukiMoc16, Theorem 2.9], there exist
![]() $A^{(1)}(K)\gt 0$
and
$A^{(1)}(K)\gt 0$
and
![]() $\epsilon ^{(1)}(K)\gt 0$
such that the following holds for any
$\epsilon ^{(1)}(K)\gt 0$
such that the following holds for any
![]() $h\in \mathop{\textrm{Harm}}\nolimits (V,\overline{\partial }_V,t\theta, C)$
$h\in \mathop{\textrm{Harm}}\nolimits (V,\overline{\partial }_V,t\theta, C)$
![]() $(t\geqslant t(K))$
:
$(t\geqslant t(K))$
:
Note that
![]() $R(h)=\overline{\partial }_V\bigl (s(h)^{-1}{\partial }_{h^C}s(h)\bigr )$
.
$R(h)=\overline{\partial }_V\bigl (s(h)^{-1}{\partial }_{h^C}s(h)\bigr )$
.
Because
![]() $s(h)$
is self-adjoint with respect to
$s(h)$
is self-adjoint with respect to
![]() $h^C$
and satisfies
$h^C$
and satisfies
![]() $\det s(h)=1$
, we have
$\det s(h)=1$
, we have
![]() ${\mathop{\textrm{Tr}}\nolimits }(s(h)-{\mathop{\textrm{id}}\nolimits })\geqslant 0$
, and
${\mathop{\textrm{Tr}}\nolimits }(s(h)-{\mathop{\textrm{id}}\nolimits })\geqslant 0$
, and
![]() ${\mathop{\textrm{Tr}}\nolimits }(s(h)-{\mathop{\textrm{id}}\nolimits }_V)=0$
holds if and only if
${\mathop{\textrm{Tr}}\nolimits }(s(h)-{\mathop{\textrm{id}}\nolimits }_V)=0$
holds if and only if
![]() $s(h)={\mathop{\textrm{id}}\nolimits }_V$
. The following holds on
$s(h)={\mathop{\textrm{id}}\nolimits }_V$
. The following holds on
![]() $Y$
(see [Reference SimpsonSim88, Lemma 3.1]):
$Y$
(see [Reference SimpsonSim88, Lemma 3.1]):
Let
![]() $K_1$
be a relatively compact open neighbourhood of
$K_1$
be a relatively compact open neighbourhood of
![]() $\overline{K}$
in
$\overline{K}$
in
![]() $Y$
. Let
$Y$
. Let
![]() $\chi :Y\to \mathbb{R}_{\geqslant 0}$
be a function such that
$\chi :Y\to \mathbb{R}_{\geqslant 0}$
be a function such that
![]() $\chi =1$
on
$\chi =1$
on
![]() $\overline{K}$
and
$\overline{K}$
and
![]() $\chi =0$
on
$\chi =0$
on
![]() $Y\setminus K_1$
. We obtain the following:
$Y\setminus K_1$
. We obtain the following:
There exist constants
![]() $A^{(2)}(K)\gt 0$
and
$A^{(2)}(K)\gt 0$
and
![]() $\epsilon ^{(2)}(K)\gt 0$
such that the following holds for any
$\epsilon ^{(2)}(K)\gt 0$
such that the following holds for any
![]() $h\in \mathop{\textrm{Harm}}\nolimits (V,\overline{\partial }_V,t\theta, C)$
$h\in \mathop{\textrm{Harm}}\nolimits (V,\overline{\partial }_V,t\theta, C)$
![]() $(t\geqslant t(K))$
:
$(t\geqslant t(K))$
:
By (10) and (11), there exist
![]() $A^{(3)}(p,K)\gt 0$
and
$A^{(3)}(p,K)\gt 0$
and
![]() $\epsilon ^{(3)}(p,K)\gt 0$
such that the following holds for any
$\epsilon ^{(3)}(p,K)\gt 0$
such that the following holds for any
![]() $h\in \mathop{\textrm{Harm}}\nolimits (V,\overline{\partial }_V,t\theta, C)$
$h\in \mathop{\textrm{Harm}}\nolimits (V,\overline{\partial }_V,t\theta, C)$
![]() $(t\geqslant t(K))$
:
$(t\geqslant t(K))$
:
By (9) and (12), there exist
![]() $A^{(4)}(p,K)\gt 0$
and
$A^{(4)}(p,K)\gt 0$
and
![]() $\epsilon ^{(4)}(p,K)\gt 0$
such that the following holds for any
$\epsilon ^{(4)}(p,K)\gt 0$
such that the following holds for any
![]() $h\in \mathop{\textrm{Harm}}\nolimits (V,\overline{\partial }_V,t\theta, C)$
$h\in \mathop{\textrm{Harm}}\nolimits (V,\overline{\partial }_V,t\theta, C)$
![]() $(t\geqslant t(K))$
:
$(t\geqslant t(K))$
:
By (12) and (13), there exist
![]() $A^{(5)}(p,K)\gt 0$
and
$A^{(5)}(p,K)\gt 0$
and
![]() $\epsilon ^{(5)}(p,K)\gt 0$
such that the following holds for any
$\epsilon ^{(5)}(p,K)\gt 0$
such that the following holds for any
![]() $h\in \mathop{\textrm{Harm}}\nolimits (V,\overline{\partial }_V,t\theta, C)$
$h\in \mathop{\textrm{Harm}}\nolimits (V,\overline{\partial }_V,t\theta, C)$
![]() $(t\geqslant t(K))$
:
$(t\geqslant t(K))$
:
Then, by using a standard bootstrapping argument, we obtain the claim of the theorem.
Corollary 3.5.
Let
![]() $t(i)\gt 0$
be any sequence such that
$t(i)\gt 0$
be any sequence such that
![]() $\lim _{i\to \infty } t(i)=\infty$
. For each
$\lim _{i\to \infty } t(i)=\infty$
. For each
![]() $t(i)$
, we take any
$t(i)$
, we take any
![]() $h_{t(i)}\in \mathop{\textrm{Harm}}\nolimits (V,\overline{\partial }_V,t(i)\theta, C)$
. Then, the sequence
$h_{t(i)}\in \mathop{\textrm{Harm}}\nolimits (V,\overline{\partial }_V,t(i)\theta, C)$
. Then, the sequence
![]() $h_{t(i)}$
is convergent to
$h_{t(i)}$
is convergent to
![]() $h^C$
in the
$h^C$
in the
![]() $C^{\infty }$
-sense on any relatively compact open subsets of
$C^{\infty }$
-sense on any relatively compact open subsets of
![]() $Y$
. The order of the convergence is estimated as in (
8
).
$Y$
. The order of the convergence is estimated as in (
8
).
4. Some estimates for harmonic bundles on a disc
This section is a preliminary for Theorem7.17.
4.1 Universal boundedness of higher derivatives of Higgs fields
For any
![]() $R\gt 0$
, we set
$R\gt 0$
, we set
![]() $B(R)=\bigl \{z\in \mathbb{C}\,\big |\,|z|\lt R\bigr \}$
. Let
$B(R)=\bigl \{z\in \mathbb{C}\,\big |\,|z|\lt R\bigr \}$
. Let
![]() $R_0\gt 0$
. Let
$R_0\gt 0$
. Let
![]() $(E,\overline{\partial }_E,\theta )$
be a Higgs bundle on
$(E,\overline{\partial }_E,\theta )$
be a Higgs bundle on
![]() $B(R_0)$
of rank
$B(R_0)$
of rank
![]() $r$
. Let
$r$
. Let
![]() $f$
be the endomorphism of
$f$
be the endomorphism of
![]() $E$
determined by
$E$
determined by
![]() $\theta =f\,dz$
. Let
$\theta =f\,dz$
. Let
![]() $C_0$
be a constant such that
$C_0$
be a constant such that
Let
![]() $h$
be a harmonic metric of
$h$
be a harmonic metric of
![]() $(E,\overline{\partial }_E,\theta )$
. Let
$(E,\overline{\partial }_E,\theta )$
. Let
![]() $\nabla _h$
denote the Chern connection of
$\nabla _h$
denote the Chern connection of
![]() $h$
. Let
$h$
. Let
![]() $R(h)$
denote the curvature of
$R(h)$
denote the curvature of
![]() $\nabla _h$
. We obtain the endomorphism
$\nabla _h$
. We obtain the endomorphism
![]() $\mathfrak R$
determined by
$\mathfrak R$
determined by
![]() $R(h)=\mathfrak R\,dz\,d{\overline{z}}$
. Let
$R(h)=\mathfrak R\,dz\,d{\overline{z}}$
. Let
![]() $f^{\dagger }_h$
denote the adjoint of
$f^{\dagger }_h$
denote the adjoint of
![]() $f$
with respect to
$f$
with respect to
![]() $h$
. Because
$h$
. Because
![]() $R(h)+[\theta, \theta ^{\dagger }_h]=0$
, we have
$R(h)+[\theta, \theta ^{\dagger }_h]=0$
, we have
![]() $\mathfrak R+[f,f^{\dagger }_h]=0$
.
$\mathfrak R+[f,f^{\dagger }_h]=0$
.
Let
![]() $g_0=dz\,d{\overline{z}}$
denote the standard Euclidean metric. We consider the
$g_0=dz\,d{\overline{z}}$
denote the standard Euclidean metric. We consider the
![]() $L_{\ell }^p$
-norm of sections of
$L_{\ell }^p$
-norm of sections of
![]() ${\mathop{\textrm{End}}\nolimits }(E)$
with respect to
${\mathop{\textrm{End}}\nolimits }(E)$
with respect to
![]() $g_0$
and
$g_0$
and
![]() $h$
, and the derivatives with respect to
$h$
, and the derivatives with respect to
![]() $\nabla _h$
.
$\nabla _h$
.
Proposition 4.1.
Let
![]() $0\lt R_1\lt R_0$
. For any
$0\lt R_1\lt R_0$
. For any
![]() $\ell \in \mathbb{Z}_{\geqslant 0}$
and
$\ell \in \mathbb{Z}_{\geqslant 0}$
and
![]() $p\geqslant 1$
, there exist
$p\geqslant 1$
, there exist
![]() $C(\ell, p)$
, depending only on
$C(\ell, p)$
, depending only on
![]() $r$
,
$r$
,
![]() $R_0$
,
$R_0$
,
![]() $R_1$
and
$R_1$
and
![]() $C_0$
, such that
$C_0$
, such that
Proof.
Let
![]() $R_2=(R_0+R_1)/2$
. By Simpson’s main estimate [Reference SimpsonSim90, Reference SimpsonSim92], there exists
$R_2=(R_0+R_1)/2$
. By Simpson’s main estimate [Reference SimpsonSim90, Reference SimpsonSim92], there exists
![]() $C_1$
, depending only on
$C_1$
, depending only on
![]() $r$
,
$r$
,
![]() $R_0$
,
$R_0$
,
![]() $R_1$
and
$R_1$
and
![]() $C_0$
, such that
$C_0$
, such that
![]() $|f|_{h}=|f^{\dagger }_h|_h\leqslant C_1$
on
$|f|_{h}=|f^{\dagger }_h|_h\leqslant C_1$
on
![]() $B(R_2)$
. We also obtain
$B(R_2)$
. We also obtain
![]() $|R(h)|_{h,g_0}=|\mathfrak R|_{h}\leqslant 2C_1^2$
on
$|R(h)|_{h,g_0}=|\mathfrak R|_{h}\leqslant 2C_1^2$
on
![]() $B(R_2)$
.
$B(R_2)$
.
We recall a result due to Uhlenbeck.
Theorem 4.2 [Reference UhlenbeckUhl82, Theorem 1.3]. Let
![]() $V$
be a vector bundle on
$V$
be a vector bundle on
![]() $B(1)$
equipped with a Hermitian metric
$B(1)$
equipped with a Hermitian metric
![]() $h_V$
and a unitary connection
$h_V$
and a unitary connection
![]() $\nabla _V$
. Let
$\nabla _V$
. Let
![]() $R(\nabla _V)$
denote the curvature of
$R(\nabla _V)$
denote the curvature of
![]() $\nabla _V$
. For
$\nabla _V$
. For
![]() $p\geqslant 1$
, let
$p\geqslant 1$
, let
![]() $\|R(\nabla _V)\|_{L^p,h_V}$
denote the
$\|R(\nabla _V)\|_{L^p,h_V}$
denote the
![]() $L^p$
-norm with respect to
$L^p$
-norm with respect to
![]() $g_0$
and
$g_0$
and
![]() $h_V$
. Then, there exist positive constants
$h_V$
. Then, there exist positive constants
![]() $c$
and
$c$
and
![]() $\kappa$
depending only on
$\kappa$
depending only on
![]() $r$
and
$r$
and
![]() $p$
such that the following holds.
$p$
such that the following holds.
-
– If
 $\|R(\nabla _V)\|_{L^p,h_V}\leqslant \kappa$
, then there exists an orthonormal frame
$\|R(\nabla _V)\|_{L^p,h_V}\leqslant \kappa$
, then there exists an orthonormal frame
 $\boldsymbol{v}$
of
$\boldsymbol{v}$
of
 $V$
such that the connection form
$V$
such that the connection form
 $A$
of
$A$
of
 $\nabla _V$
with respect to
$\nabla _V$
with respect to
 $\boldsymbol{v}$
satisfies (i)
$\boldsymbol{v}$
satisfies (i)
 $d^{\ast }A=0$
and (ii)
$d^{\ast }A=0$
and (ii)
 $\|A\|_{L_1^p}\leqslant c\|R(\nabla _V)\|_{L^p}$
.
$\|A\|_{L_1^p}\leqslant c\|R(\nabla _V)\|_{L^p}$
.
We choose
![]() $T\gt 0$
such that
$T\gt 0$
such that
![]() $100T^{-1}C_1^2\lt \kappa$
and
$100T^{-1}C_1^2\lt \kappa$
and
![]() $T(R_0-R_2)\gt 100$
. Let
$T(R_0-R_2)\gt 100$
. Let
![]() $\varphi _T:\mathbb{C}_w\to \mathbb{C}_z$
be defined by
$\varphi _T:\mathbb{C}_w\to \mathbb{C}_z$
be defined by
![]() $\varphi _T(w)=T^{-1}z$
. We consider
$\varphi _T(w)=T^{-1}z$
. We consider
![]() $(\widetilde{E},\overline{\partial }_{\widetilde{E}},\widetilde{\theta },\widetilde{h}) =\varphi _T^{\ast }(E,\overline{\partial }_E,\theta, h)$
on
$(\widetilde{E},\overline{\partial }_{\widetilde{E}},\widetilde{\theta },\widetilde{h}) =\varphi _T^{\ast }(E,\overline{\partial }_E,\theta, h)$
on
![]() $B(TR_0)$
. Let
$B(TR_0)$
. Let
![]() $w_0\in B(TR_2-1)$
. Let
$w_0\in B(TR_2-1)$
. Let
![]() $p\gt 2$
. Let
$p\gt 2$
. Let
![]() $\boldsymbol{v}^{(w_0)}$
be an orthonormal frame of
$\boldsymbol{v}^{(w_0)}$
be an orthonormal frame of
![]() $\widetilde{E}_{|D(w_0,1)}$
as in Theorem4.2 for the metric
$\widetilde{E}_{|D(w_0,1)}$
as in Theorem4.2 for the metric
![]() $\widetilde{h}$
and the connection
$\widetilde{h}$
and the connection
![]() $\nabla _{\widetilde{h}}$
. Let
$\nabla _{\widetilde{h}}$
. Let
![]() $\mathcal{A}^{(w_0)}$
and
$\mathcal{A}^{(w_0)}$
and
![]() $\mathcal{R}^{(w_0)}$
denote the connection form and the curvature form of
$\mathcal{R}^{(w_0)}$
denote the connection form and the curvature form of
![]() $\nabla _{\widetilde{h}}$
with respect to
$\nabla _{\widetilde{h}}$
with respect to
![]() $\boldsymbol{v}^{(w_0)}$
. We have
$\boldsymbol{v}^{(w_0)}$
. We have
Let
![]() $\Theta ^{(w_0)}$
denote the matrix-valued
$\Theta ^{(w_0)}$
denote the matrix-valued
![]() $(1,0)$
-form determined by
$(1,0)$
-form determined by
![]() $\widetilde{\theta }\boldsymbol{v}^{(w_0)}=\boldsymbol{v}^{(w_0)}\Theta ^{(w_0)}$
. We have the decomposition
$\widetilde{\theta }\boldsymbol{v}^{(w_0)}=\boldsymbol{v}^{(w_0)}\Theta ^{(w_0)}$
. We have the decomposition
![]() $\mathcal{A}^{(w_0)}=\mathcal{A}^{(w_0)}_w\,dw+ \mathcal{A}^{(w_0)}_{\overline{w}}\,d\overline{w}$
. We have
$\mathcal{A}^{(w_0)}=\mathcal{A}^{(w_0)}_w\,dw+ \mathcal{A}^{(w_0)}_{\overline{w}}\,d\overline{w}$
. We have
![]() $\mathcal{A}^{(w_0)}_{w}= -{}^{t}\!\overline{\mathcal{A}^{(w_0)}_{\overline{w}}}$
. Because
$\mathcal{A}^{(w_0)}_{w}= -{}^{t}\!\overline{\mathcal{A}^{(w_0)}_{\overline{w}}}$
. Because
![]() $\overline{\partial }\widetilde{\theta }=0$
, the following holds:
$\overline{\partial }\widetilde{\theta }=0$
, the following holds:
We also have
Then, by a standard bootstrapping argument, we can prove that for any
![]() $\ell$
there exists
$\ell$
there exists
![]() $C_2(\ell )$
, depending only on
$C_2(\ell )$
, depending only on
![]() $\ell$
and
$\ell$
and
![]() $r$
such that
$r$
such that
We obtain a desired estimate for
![]() $\|f_{|B(R_1)}\|_{L_{\ell }^p}$
, which implies a desired estimate for
$\|f_{|B(R_1)}\|_{L_{\ell }^p}$
, which implies a desired estimate for
![]() $\|f^{\dagger }_{h|B(R_1)}\|_{L_{\ell }^p}$
. Because
$\|f^{\dagger }_{h|B(R_1)}\|_{L_{\ell }^p}$
. Because
![]() $\mathfrak R+[f,f^{\dagger }_h]=0$
, we also obtain a desired estimate for
$\mathfrak R+[f,f^{\dagger }_h]=0$
, we also obtain a desired estimate for
![]() $\|\mathfrak R_{|B(R_1)}\|_{L_{\ell }^p}$
.
$\|\mathfrak R_{|B(R_1)}\|_{L_{\ell }^p}$
.
4.2 Difference of two families of large-scale solutions on a disc
Let
![]() $R_0\gt 0$
. Let
$R_0\gt 0$
. Let
![]() $(E,\overline{\partial }_E,\theta )$
be a Higgs bundle on
$(E,\overline{\partial }_E,\theta )$
be a Higgs bundle on
![]() $B(R_0)$
of rank
$B(R_0)$
of rank
![]() $r$
. Let
$r$
. Let
![]() $f$
be the endomorphism of
$f$
be the endomorphism of
![]() $E$
determined by
$E$
determined by
![]() $\theta =f\,dz$
. Let
$\theta =f\,dz$
. Let
![]() $C_0$
be a constant such that
$C_0$
be a constant such that
Let
![]() $h_{\det (E)}$
be a flat metric of
$h_{\det (E)}$
be a flat metric of
![]() $\det (E)$
. Let
$\det (E)$
. Let
![]() $h_{0,t}$
$h_{0,t}$
![]() $(t\gt 0)$
be harmonic metrics of
$(t\gt 0)$
be harmonic metrics of
![]() $(E,\overline{\partial }_E,t\theta )$
such that
$(E,\overline{\partial }_E,t\theta )$
such that
![]() $\det (h_{0,t})=h_{\det (E)}$
. Let
$\det (h_{0,t})=h_{\det (E)}$
. Let
![]() $\nabla ^{0,t}$
denote the Chern connection of
$\nabla ^{0,t}$
denote the Chern connection of
![]() $(E,\overline{\partial }_E,h_{0,t})$
. For any section
$(E,\overline{\partial }_E,h_{0,t})$
. For any section
![]() $u$
of
$u$
of
![]() ${\mathop{\textrm{End}}\nolimits }(E)$
and for any element
${\mathop{\textrm{End}}\nolimits }(E)$
and for any element
![]() $\boldsymbol{\kappa }=(\kappa _1,\kappa _2,\ldots, \kappa _{\ell }) \in \{z,{\overline{z}}\}^{\ell }$
, we set
$\boldsymbol{\kappa }=(\kappa _1,\kappa _2,\ldots, \kappa _{\ell }) \in \{z,{\overline{z}}\}^{\ell }$
, we set
Theorem 4.3.
Let
![]() $0\lt R_1\lt R_0$
. Let
$0\lt R_1\lt R_0$
. Let
![]() $C_1,\epsilon _1\gt 0$
. For any
$C_1,\epsilon _1\gt 0$
. For any
![]() $\ell \in \mathbb{Z}_{\geqslant 0}$
, there exist positive constants
$\ell \in \mathbb{Z}_{\geqslant 0}$
, there exist positive constants
![]() $C(\ell ),\epsilon (\ell )\gt 0$
, depending only on
$C(\ell ),\epsilon (\ell )\gt 0$
, depending only on
![]() $r$
,
$r$
,
![]() $C_0,C_1,\epsilon _1$
and
$C_0,C_1,\epsilon _1$
and
![]() $\ell$
such that the following holds.
$\ell$
such that the following holds.
-
– Let
 $t(i)\gt 0$
be an increasing sequence such that
$t(i)\gt 0$
be an increasing sequence such that
 $t(i)\to \infty$
as
$t(i)\to \infty$
as
 $i\to \infty$
. We also assume that
$i\to \infty$
. We also assume that
 $t(1)(R_0-R_1)\gt 100$
. Let
$t(1)(R_0-R_1)\gt 100$
. Let
 $h_{t(i)}$
be harmonic metrics of
$h_{t(i)}$
be harmonic metrics of
 $(E,\overline{\partial }_E,t(i)\theta )$
such that
$(E,\overline{\partial }_E,t(i)\theta )$
such that
 $\det (h_{t(i)})=h_{\det (E)}$
. Assume the following on
$\det (h_{t(i)})=h_{\det (E)}$
. Assume the following on
 $B(R_0)\setminus B(R_1)$
:(19)Then, the following holds on
$B(R_0)\setminus B(R_1)$
:(19)Then, the following holds on \begin{align} \bigl |s(h_{0,t(i)},h_{t(i)})-{\mathop{\textrm{id}}\nolimits } \bigr |_{h_{0,t(i)}} \leqslant C_1\exp (-\epsilon _1t(i)). \end{align}
\begin{align} \bigl |s(h_{0,t(i)},h_{t(i)})-{\mathop{\textrm{id}}\nolimits } \bigr |_{h_{0,t(i)}} \leqslant C_1\exp (-\epsilon _1t(i)). \end{align}
 $B(R_1)$
for any
$B(R_1)$
for any
 $\boldsymbol{\kappa }\in \{z,{\overline{z}}\}^{\ell }$
:
$\boldsymbol{\kappa }\in \{z,{\overline{z}}\}^{\ell }$
: \begin{align*} \Bigl | \nabla ^{0,t(i)}_{\boldsymbol {\kappa }}\bigl ( s(h_{0,t(i)},h_{t(i)})-{\mathop {\textrm {id}}\nolimits } \bigr ) \Bigr |_{h_{0,t(i)}} \leqslant C(\ell ) \exp \bigl (-\epsilon (\ell )t(i)\bigr ). \end{align*}
\begin{align*} \Bigl | \nabla ^{0,t(i)}_{\boldsymbol {\kappa }}\bigl ( s(h_{0,t(i)},h_{t(i)})-{\mathop {\textrm {id}}\nolimits } \bigr ) \Bigr |_{h_{0,t(i)}} \leqslant C(\ell ) \exp \bigl (-\epsilon (\ell )t(i)\bigr ). \end{align*}
4.2.1 The case
 $\ell =0$
$\ell =0$
To simplify the notation we set
![]() $s_i=s(h_{0,t(i)},h_{t(i)})$
. By (19), there exist
$s_i=s(h_{0,t(i)},h_{t(i)})$
. By (19), there exist
![]() $C'(0),\epsilon '(0)\gt 0$
, depending only on
$C'(0),\epsilon '(0)\gt 0$
, depending only on
![]() $r$
,
$r$
,
![]() $C_1$
and
$C_1$
and
![]() $\epsilon _1$
, such that the following holds on
$\epsilon _1$
, such that the following holds on
![]() $B(R_0)\setminus B(R_1)$
:
$B(R_0)\setminus B(R_1)$
:
By [Reference SimpsonSim88, Lemma 3.1], we have
In particular,
![]() ${\mathop{\textrm{Tr}}\nolimits }\bigl (s_i-{\mathop{\textrm{id}}\nolimits }_E\bigr )$
is a subharmonic function on
${\mathop{\textrm{Tr}}\nolimits }\bigl (s_i-{\mathop{\textrm{id}}\nolimits }_E\bigr )$
is a subharmonic function on
![]() $B(R_0)$
. By the maximum principle of subharmonic functions, (20) holds on
$B(R_0)$
. By the maximum principle of subharmonic functions, (20) holds on
![]() $B(R_0)$
. Because
$B(R_0)$
. Because
![]() $\det (s_i)=1$
, we obtain the claim in the case
$\det (s_i)=1$
, we obtain the claim in the case
![]() $\ell =0$
.
$\ell =0$
.
4.2.2 Estimates for
 $L^2$
-norms
$L^2$
-norms
We set
![]() $R_2=(R_0+R_1)/2$
and
$R_2=(R_0+R_1)/2$
and
![]() $R_3=(R_0+R_2)/2$
. Let
$R_3=(R_0+R_2)/2$
. Let
![]() $\chi :\mathbb{C}\to \mathbb{R}_{\geqslant 0}$
be a
$\chi :\mathbb{C}\to \mathbb{R}_{\geqslant 0}$
be a
![]() $C^{\infty }$
-function such that
$C^{\infty }$
-function such that
![]() $\chi (z)=1$
$\chi (z)=1$
![]() $(|z|\leqslant R_2)$
and
$(|z|\leqslant R_2)$
and
![]() $\chi (z)=0$
$\chi (z)=0$
![]() $(|z|\geqslant R_3)$
. Let
$(|z|\geqslant R_3)$
. Let
![]() $g_z=dz\,d{\overline{z}}$
be the standard Euclidean metric. By using [Reference SimpsonSim88, Lemma 3.1], we obtain
$g_z=dz\,d{\overline{z}}$
be the standard Euclidean metric. By using [Reference SimpsonSim88, Lemma 3.1], we obtain
 \begin{align} &\int _{B(R_2)} \Bigl ( \bigl | \overline{\partial }(s_i) s_i^{-1/2} \bigr |^2_{h_{0,t(i)},g_z} +\bigl | [t(i)\theta, s_i]s_i^{-1/2} \bigr |^2_{h_{0,t(i)},g_z} \Bigr )\mathop{\textrm{dvol}}\nolimits _{g_z} \leqslant \nonumber \\[5pt] &\qquad \qquad \qquad \qquad \int _{B(R_3)\setminus B(R_2)} \bigl |{\partial }_z{\partial }_{{\overline{z}}}(\chi ) \bigr |\cdot \bigl ({\mathop{\textrm{Tr}}\nolimits }(s_i-{\mathop{\textrm{id}}\nolimits }_E) \bigr )\mathop{\textrm{dvol}}\nolimits _{g_z}. \end{align}
\begin{align} &\int _{B(R_2)} \Bigl ( \bigl | \overline{\partial }(s_i) s_i^{-1/2} \bigr |^2_{h_{0,t(i)},g_z} +\bigl | [t(i)\theta, s_i]s_i^{-1/2} \bigr |^2_{h_{0,t(i)},g_z} \Bigr )\mathop{\textrm{dvol}}\nolimits _{g_z} \leqslant \nonumber \\[5pt] &\qquad \qquad \qquad \qquad \int _{B(R_3)\setminus B(R_2)} \bigl |{\partial }_z{\partial }_{{\overline{z}}}(\chi ) \bigr |\cdot \bigl ({\mathop{\textrm{Tr}}\nolimits }(s_i-{\mathop{\textrm{id}}\nolimits }_E) \bigr )\mathop{\textrm{dvol}}\nolimits _{g_z}. \end{align}
Hence, there exist
![]() $C_5\gt 0,\epsilon _5\gt 0$
such that
$C_5\gt 0,\epsilon _5\gt 0$
such that
4.2.3 Rescaling
To study the derivatives, for any
![]() $t\gt t(1)$
, we define the map
$t\gt t(1)$
, we define the map
![]() $\rho _t:\mathbb{C}_w\to \mathbb{C}_z$
by
$\rho _t:\mathbb{C}_w\to \mathbb{C}_z$
by
![]() $\rho _t(w)=t^{-1}w$
. We have
$\rho _t(w)=t^{-1}w$
. We have
![]() $\rho _t^{-1}(B(R))=B(tR)$
. We use the standard Euclidean metric
$\rho _t^{-1}(B(R))=B(tR)$
. We use the standard Euclidean metric
![]() $g_w=dw\,d\overline{w}$
on
$g_w=dw\,d\overline{w}$
on
![]() $\mathbb{C}_w$
.
$\mathbb{C}_w$
.
We set
![]() $\widetilde{E}_{t}=\rho _t^{\ast }(E)$
on
$\widetilde{E}_{t}=\rho _t^{\ast }(E)$
on
![]() $B(tR_0)$
. It is equipped with the Higgs field
$B(tR_0)$
. It is equipped with the Higgs field
![]() $\widetilde{\theta }_t=\rho _t^{\ast }(t\theta )$
. We have
$\widetilde{\theta }_t=\rho _t^{\ast }(t\theta )$
. We have
![]() $\widetilde{\theta }_t=\rho _t^{\ast }(f)\,dw$
. We have the harmonic metrics
$\widetilde{\theta }_t=\rho _t^{\ast }(f)\,dw$
. We have the harmonic metrics
![]() $\widetilde{h}_{0,t}=\varphi _t^{\ast }(h_{0,t})$
of the Higgs bundles
$\widetilde{h}_{0,t}=\varphi _t^{\ast }(h_{0,t})$
of the Higgs bundles
![]() $(\widetilde{E}_t,\overline{\partial }_{\widetilde{E}_t},\widetilde{\theta }_t)$
. Let
$(\widetilde{E}_t,\overline{\partial }_{\widetilde{E}_t},\widetilde{\theta }_t)$
. Let
![]() $\widetilde{\nabla }^{0,t}$
denote the Chern connection of
$\widetilde{\nabla }^{0,t}$
denote the Chern connection of
![]() $(\widetilde{E}_t,\overline{\partial }_{\widetilde{E}_t},\widetilde{h}_{0,t})$
.
$(\widetilde{E}_t,\overline{\partial }_{\widetilde{E}_t},\widetilde{h}_{0,t})$
.
By Simpson’s main estimate, there exists
![]() $C_{10}\gt 0$
, depending only on
$C_{10}\gt 0$
, depending only on
![]() $r$
and
$r$
and
![]() $C_0$
, such that the following holds on
$C_0$
, such that the following holds on
![]() $B(tR_0-1)$
:
$B(tR_0-1)$
:
Let
![]() $R(\widetilde{h}_{0,t})$
denote the curvature of the Chern connection of
$R(\widetilde{h}_{0,t})$
denote the curvature of the Chern connection of
![]() $(\widetilde{E}_{t},\overline{\partial }_{\widetilde{E}_{t}}, \widetilde{h}_{0,t})$
. We have the following equality:
$(\widetilde{E}_{t},\overline{\partial }_{\widetilde{E}_{t}}, \widetilde{h}_{0,t})$
. We have the following equality:
By (24) and (25), we have the following on
![]() $B(tR_0-1)$
:
$B(tR_0-1)$
:
We also have the universal estimates for higher derivatives of
![]() $\widetilde{\theta }$
and
$\widetilde{\theta }$
and
![]() $R(\widetilde{h}_{0,t})$
as in Proposition 4.1.
$R(\widetilde{h}_{0,t})$
as in Proposition 4.1.
4.2.4 Estimates for higher derivatives
We also have the harmonic metrics
![]() $\widetilde{h}_{t(i)}=\varphi _{t(i)}^{\ast }(h_{t(i)})$
of
$\widetilde{h}_{t(i)}=\varphi _{t(i)}^{\ast }(h_{t(i)})$
of
![]() $(\widetilde{E}_{t(i)},\overline{\partial }_{\widetilde{E}_{t(i)}},\widetilde{\theta }_{t(i)})$
. Let
$(\widetilde{E}_{t(i)},\overline{\partial }_{\widetilde{E}_{t(i)}},\widetilde{\theta }_{t(i)})$
. Let
![]() $\widetilde{s}_i=\varphi _{t(i)}^{\ast }(s_i)$
. We have
$\widetilde{s}_i=\varphi _{t(i)}^{\ast }(s_i)$
. We have
![]() $\widetilde{h}_{t(i)}=\widetilde{h}_{0,t(i)}\widetilde{s}_i$
. By (23), we have
$\widetilde{h}_{t(i)}=\widetilde{h}_{0,t(i)}\widetilde{s}_i$
. By (23), we have
This implies
Let
![]() $R(\widetilde{h}_{t(i)})$
denote the curvature of the Chern connection of
$R(\widetilde{h}_{t(i)})$
denote the curvature of the Chern connection of
![]() $(\widetilde{E}_{t(i)},\overline{\partial }_{\widetilde{E}_{t(i)}},\widetilde{h}_{t(i)})$
. We have
$(\widetilde{E}_{t(i)},\overline{\partial }_{\widetilde{E}_{t(i)}},\widetilde{h}_{t(i)})$
. We have
Note that
We obtain
 \begin{align} \overline{\partial }\bigl ( \widetilde{s}_i^{-1}{\partial }_{\widetilde{h}_{0,t(i)}} \widetilde{s}_i \bigr ) &=R(\widetilde{h}_{t(i)})- R(\widetilde{h}_{0,t(i)}) =-\Bigl [ \widetilde{\theta }_{t(i)}, \widetilde{s}_i^{-1} (\widetilde{\theta }_{t(i)})^{\dagger }_{\widetilde{h}_{0,t(i)}} \widetilde{s}_i -(\widetilde{\theta }_{t(i)})^{\dagger }_{\widetilde{h}_{0,t(i)}} \Bigr ] \nonumber \\[5pt] & = -\Bigl [ \widetilde{\theta }_{t(i)}, \widetilde{s}_i^{-1} \bigl [ (\widetilde{\theta }_{t(i)})^{\dagger }_{\widetilde{h}_{0,t(i)}}, \widetilde{s}_i-{\mathop{\textrm{id}}\nolimits } \bigr ] \Bigr ]. \end{align}
\begin{align} \overline{\partial }\bigl ( \widetilde{s}_i^{-1}{\partial }_{\widetilde{h}_{0,t(i)}} \widetilde{s}_i \bigr ) &=R(\widetilde{h}_{t(i)})- R(\widetilde{h}_{0,t(i)}) =-\Bigl [ \widetilde{\theta }_{t(i)}, \widetilde{s}_i^{-1} (\widetilde{\theta }_{t(i)})^{\dagger }_{\widetilde{h}_{0,t(i)}} \widetilde{s}_i -(\widetilde{\theta }_{t(i)})^{\dagger }_{\widetilde{h}_{0,t(i)}} \Bigr ] \nonumber \\[5pt] & = -\Bigl [ \widetilde{\theta }_{t(i)}, \widetilde{s}_i^{-1} \bigl [ (\widetilde{\theta }_{t(i)})^{\dagger }_{\widetilde{h}_{0,t(i)}}, \widetilde{s}_i-{\mathop{\textrm{id}}\nolimits } \bigr ] \Bigr ]. \end{align}
Hence, there exist
![]() $C_{11}\gt 0$
and
$C_{11}\gt 0$
and
![]() $\epsilon _{11}\gt 0$
such that the following holds on
$\epsilon _{11}\gt 0$
such that the following holds on
![]() $B(t(i)R_0-1)$
:
$B(t(i)R_0-1)$
:
For any
![]() $w_0\in \mathbb{C}_w$
, we set
$w_0\in \mathbb{C}_w$
, we set
![]() $D(w_0,T)=\{|w-w_0|\lt T\}$
. By (26), (28) and (30), for any
$D(w_0,T)=\{|w-w_0|\lt T\}$
. By (26), (28) and (30), for any
![]() $p\geqslant 2$
, there exist
$p\geqslant 2$
, there exist
![]() $C_{12}(p)\gt 0,\epsilon _{12}(p)\gt 0$
such that the following holds for any
$C_{12}(p)\gt 0,\epsilon _{12}(p)\gt 0$
such that the following holds for any
![]() $w_0\in B(t(i)R_2-1)$
:
$w_0\in B(t(i)R_2-1)$
:
By (31) and the estimate in the case
![]() $\ell =0$
, for any
$\ell =0$
, for any
![]() $p\gt 1$
, there exist
$p\gt 1$
, there exist
![]() $C_{13}(p)\gt 0,\epsilon _{13}(p)\gt 0$
such that the following holds for any
$C_{13}(p)\gt 0,\epsilon _{13}(p)\gt 0$
such that the following holds for any
![]() $w_0\in B(t(i)R_2-1)$
:
$w_0\in B(t(i)R_2-1)$
:
By a standard bootstrapping argument, for any
![]() $p\gt 1$
and
$p\gt 1$
and
![]() $\ell \in \mathbb{Z}_{\geqslant 2}$
, there exist
$\ell \in \mathbb{Z}_{\geqslant 2}$
, there exist
![]() $C_{14}(\ell, p)\gt 0,\epsilon _{14}(\ell, p)\gt 0$
such that the following holds for any
$C_{14}(\ell, p)\gt 0,\epsilon _{14}(\ell, p)\gt 0$
such that the following holds for any
![]() $w_0\in B(t(i)R_2-1)$
:
$w_0\in B(t(i)R_2-1)$
:
Then, we obtain the claim of Theorem4.3.
5. Decomposable filtered extensions
5.1 Meromorphic extensions and filtered extensions
5.1.1 Vector bundles
Let
![]() $U\subset \mathbb{C}$
be a simply connected open neighbourhood of
$U\subset \mathbb{C}$
be a simply connected open neighbourhood of
![]() $0$
. We set
$0$
. We set
![]() $U^{\ast }=U\setminus \{0\}$
. Let
$U^{\ast }=U\setminus \{0\}$
. Let
![]() $\iota :U^{\ast }\to U$
denote the inclusion. Let
$\iota :U^{\ast }\to U$
denote the inclusion. Let
![]() $V$
be a locally free
$V$
be a locally free
![]() $\mathcal{O}_{U^{\ast }}$
-module of rank
$\mathcal{O}_{U^{\ast }}$
-module of rank
![]() $r$
. We obtain a locally free
$r$
. We obtain a locally free
![]() $\iota _{\ast }\mathcal{O}_{U^{\ast }}$
-module
$\iota _{\ast }\mathcal{O}_{U^{\ast }}$
-module
![]() $\iota _{\ast }(V)$
. A meromorphic (respectively smooth) extension of
$\iota _{\ast }(V)$
. A meromorphic (respectively smooth) extension of
![]() $V$
is defined to be a locally free
$V$
is defined to be a locally free
![]() $\mathcal{O}_{U}(\ast 0)$
-submodule (respectively
$\mathcal{O}_{U}(\ast 0)$
-submodule (respectively
![]() $\mathcal{O}_U$
-submodule)
$\mathcal{O}_U$
-submodule)
![]() $\mathcal{V}\subset \iota _{\ast }(V)$
such that
$\mathcal{V}\subset \iota _{\ast }(V)$
such that
![]() $\mathcal{V}_{|U^{\ast }}=V$
. A filtered extension of
$\mathcal{V}_{|U^{\ast }}=V$
. A filtered extension of
![]() $V$
is defined to be a meromorphic extension
$V$
is defined to be a meromorphic extension
![]() $\mathcal{V}$
equipped with a filtered bundle
$\mathcal{V}$
equipped with a filtered bundle
![]() $\mathcal{P}_{\ast }(\mathcal{V})$
over
$\mathcal{P}_{\ast }(\mathcal{V})$
over
![]() $\mathcal{V}$
.
$\mathcal{V}$
.
Example 5.1. The
![]() $\mathcal{O}_U(\ast 0)$
-submodule
$\mathcal{O}_U(\ast 0)$
-submodule
![]() $\mathcal{O}_U(\ast 0)\exp (z^{-1})\subset \iota _{\ast }(\mathcal{O}_{U^{\ast }})$
is a meromorphic extension of
$\mathcal{O}_U(\ast 0)\exp (z^{-1})\subset \iota _{\ast }(\mathcal{O}_{U^{\ast }})$
is a meromorphic extension of
![]() $\mathcal{O}_{U^{\ast }}$
, which is different from
$\mathcal{O}_{U^{\ast }}$
, which is different from
![]() $\mathcal{O}_U(\ast 0)\subset \iota _{\ast }(\mathcal{O}_{U^{\ast }})$
.
$\mathcal{O}_U(\ast 0)\subset \iota _{\ast }(\mathcal{O}_{U^{\ast }})$
.
For a positive integer
![]() $\ell$
, let
$\ell$
, let
![]() $\varphi _{\ell }:\mathbb{C}\to \mathbb{C}$
be defined by
$\varphi _{\ell }:\mathbb{C}\to \mathbb{C}$
be defined by
![]() $\varphi _{\ell }(\zeta )=\zeta ^{\ell }$
. We set
$\varphi _{\ell }(\zeta )=\zeta ^{\ell }$
. We set
![]() $U^{(\ell )}=\varphi _{\ell }^{-1}(U)$
and
$U^{(\ell )}=\varphi _{\ell }^{-1}(U)$
and
![]() $U^{(\ell )\ast }=U^{(\ell )}\setminus \{0\}$
. The induced morphisms
$U^{(\ell )\ast }=U^{(\ell )}\setminus \{0\}$
. The induced morphisms
![]() $U^{(\ell )}\to U$
and
$U^{(\ell )}\to U$
and
![]() $U^{(\ell )\ast }\to U^{\ast }$
are also denoted by
$U^{(\ell )\ast }\to U^{\ast }$
are also denoted by
![]() $\varphi _{\ell }$
. Let
$\varphi _{\ell }$
. Let
![]() $\mathop{\textrm{Gal}}\nolimits (\ell )$
denote the Galois group of the ramified covering
$\mathop{\textrm{Gal}}\nolimits (\ell )$
denote the Galois group of the ramified covering
![]() $\varphi _{\ell }$
. Namely, we put
$\varphi _{\ell }$
. Namely, we put
![]() $\mathop{\textrm{Gal}}\nolimits (\ell )=\{a\in \mathbb{C}^{\ast }\,|\,a^{\ell }=1\}$
, and we consider the action of
$\mathop{\textrm{Gal}}\nolimits (\ell )=\{a\in \mathbb{C}^{\ast }\,|\,a^{\ell }=1\}$
, and we consider the action of
![]() $\mathop{\textrm{Gal}}\nolimits (\ell )$
on
$\mathop{\textrm{Gal}}\nolimits (\ell )$
on
![]() $U^{(\ell )}$
by the multiplication on the coordinate
$U^{(\ell )}$
by the multiplication on the coordinate
![]() $\zeta$
. Let
$\zeta$
. Let
![]() $\iota ^{(\ell )}:U^{(\ell )\ast }\to U^{(\ell )}$
denote the inclusion. We set
$\iota ^{(\ell )}:U^{(\ell )\ast }\to U^{(\ell )}$
denote the inclusion. We set
![]() $V^{(\ell )}:=\varphi _{\ell }^{\ast }(V)$
, which is naturally
$V^{(\ell )}:=\varphi _{\ell }^{\ast }(V)$
, which is naturally
![]() $\mathop{\textrm{Gal}}\nolimits (\ell )$
-equivariant. The
$\mathop{\textrm{Gal}}\nolimits (\ell )$
-equivariant. The
![]() $(\iota ^{(\ell )})_{\ast }\mathcal{O}_{U^{(\ell )\ast }}$
-module
$(\iota ^{(\ell )})_{\ast }\mathcal{O}_{U^{(\ell )\ast }}$
-module
![]() $(\iota ^{(\ell )})_{\ast }(V^{(\ell )})$
is also
$(\iota ^{(\ell )})_{\ast }(V^{(\ell )})$
is also
![]() $\mathop{\textrm{Gal}}\nolimits (\ell )$
-equivariant. A
$\mathop{\textrm{Gal}}\nolimits (\ell )$
-equivariant. A
![]() $\mathop{\textrm{Gal}}\nolimits (\ell )$
-equivariant meromorphic extension of
$\mathop{\textrm{Gal}}\nolimits (\ell )$
-equivariant meromorphic extension of
![]() $V^{(\ell )}$
is defined to be a locally free
$V^{(\ell )}$
is defined to be a locally free
![]() $\mathcal{O}_{U^{(\ell )}}(\ast 0)$
-submodule
$\mathcal{O}_{U^{(\ell )}}(\ast 0)$
-submodule
![]() $\mathcal{V}^{(\ell )}\subset \iota ^{(\ell )}_{\ast }(V^{(\ell )})$
which is preserved by the
$\mathcal{V}^{(\ell )}\subset \iota ^{(\ell )}_{\ast }(V^{(\ell )})$
which is preserved by the
![]() $\mathop{\textrm{Gal}}\nolimits (\ell )$
-action. A
$\mathop{\textrm{Gal}}\nolimits (\ell )$
-action. A
![]() $\mathop{\textrm{Gal}}\nolimits (\ell )$
-equivariant filtered extension of
$\mathop{\textrm{Gal}}\nolimits (\ell )$
-equivariant filtered extension of
![]() $V^{(\ell )}$
is defined to be a filtered bundle
$V^{(\ell )}$
is defined to be a filtered bundle
![]() $\mathcal{P}_{\ast }(\mathcal{V}^{(\ell )})$
over a
$\mathcal{P}_{\ast }(\mathcal{V}^{(\ell )})$
over a
![]() $\mathop{\textrm{Gal}}\nolimits (\ell )$
-equivariant meromorphic extension
$\mathop{\textrm{Gal}}\nolimits (\ell )$
-equivariant meromorphic extension
![]() $\mathcal{V}^{(\ell )}$
of
$\mathcal{V}^{(\ell )}$
of
![]() $V^{(\ell )}$
such that each
$V^{(\ell )}$
such that each
![]() $\mathcal{P}_{a}\mathcal{V}^{(\ell )}$
is preserved by the
$\mathcal{P}_{a}\mathcal{V}^{(\ell )}$
is preserved by the
![]() $\mathop{\textrm{Gal}}\nolimits (\ell )$
-action.
$\mathop{\textrm{Gal}}\nolimits (\ell )$
-action.
A meromorphic extension
![]() $\mathcal{V}$
of
$\mathcal{V}$
of
![]() $V$
induces a
$V$
induces a
![]() $\mathop{\textrm{Gal}}\nolimits (\ell )$
-equivariant meromorphic extension
$\mathop{\textrm{Gal}}\nolimits (\ell )$
-equivariant meromorphic extension
![]() $\varphi _{\ell }^{\ast }(\mathcal{V})$
of
$\varphi _{\ell }^{\ast }(\mathcal{V})$
of
![]() $V^{(\ell )}$
. Conversely, for any
$V^{(\ell )}$
. Conversely, for any
![]() $\mathop{\textrm{Gal}}\nolimits (\ell )$
-equivariant meromorphic extension
$\mathop{\textrm{Gal}}\nolimits (\ell )$
-equivariant meromorphic extension
![]() $\mathcal{V}^{(\ell )}$
of
$\mathcal{V}^{(\ell )}$
of
![]() $V^{(\ell )}$
, we obtain the
$V^{(\ell )}$
, we obtain the
![]() $\mathcal{O}_{U}(\ast 0)$
-module
$\mathcal{O}_{U}(\ast 0)$
-module
![]() $\varphi _{\ell \ast }(\mathcal{V}^{(\ell )})$
equipped with the
$\varphi _{\ell \ast }(\mathcal{V}^{(\ell )})$
equipped with the
![]() $\mathop{\textrm{Gal}}\nolimits (\ell )$
-action. The
$\mathop{\textrm{Gal}}\nolimits (\ell )$
-action. The
![]() $\mathop{\textrm{Gal}}\nolimits (\ell )$
-invariant part
$\mathop{\textrm{Gal}}\nolimits (\ell )$
-invariant part
![]() $\varphi _{\ell \ast }(\mathcal{V}^{(\ell )})^{\mathop{\textrm{Gal}}\nolimits (\ell )}$
is called the descent of
$\varphi _{\ell \ast }(\mathcal{V}^{(\ell )})^{\mathop{\textrm{Gal}}\nolimits (\ell )}$
is called the descent of
![]() $\mathcal{V}^{(\ell )}$
which is a meromorphic extension of
$\mathcal{V}^{(\ell )}$
which is a meromorphic extension of
![]() $V$
.
$V$
.
Lemma 5.2.
For a meromorphic extension
![]() $\mathcal{V}$
of
$\mathcal{V}$
of
![]() $V$
, the descent of
$V$
, the descent of
![]() $\varphi _{\ell }^{\ast }(\mathcal{V})$
equals
$\varphi _{\ell }^{\ast }(\mathcal{V})$
equals
![]() $\mathcal{V}$
. For a
$\mathcal{V}$
. For a
![]() $\mathop{\textrm{Gal}}\nolimits (\ell )$
-equivariant meromorphic extension
$\mathop{\textrm{Gal}}\nolimits (\ell )$
-equivariant meromorphic extension
![]() $\mathcal{V}^{(\ell )}$
of
$\mathcal{V}^{(\ell )}$
of
![]() $V^{(\ell )}$
,
$V^{(\ell )}$
,
![]() $\varphi _{\ell }^{\ast }\bigl ( \varphi _{\ell \ast }(\mathcal{V}^{(\ell )})^{\mathop{\textrm{Gal}}\nolimits (\ell )} \bigr )$
equals
$\varphi _{\ell }^{\ast }\bigl ( \varphi _{\ell \ast }(\mathcal{V}^{(\ell )})^{\mathop{\textrm{Gal}}\nolimits (\ell )} \bigr )$
equals
![]() $\mathcal{V}^{(\ell )}$
. These procedures induce an equivalence between meromorphic extensions of
$\mathcal{V}^{(\ell )}$
. These procedures induce an equivalence between meromorphic extensions of
![]() $V$
and
$V$
and
![]() $\mathop{\textrm{Gal}}\nolimits (\ell )$
-equivariant meromorphic extensions of
$\mathop{\textrm{Gal}}\nolimits (\ell )$
-equivariant meromorphic extensions of
![]() $V^{(\ell )}$
.
$V^{(\ell )}$
.
For a filtered extension
![]() $\mathcal{P}_{\ast }\mathcal{V}$
of
$\mathcal{P}_{\ast }\mathcal{V}$
of
![]() $V$
, we obtain a
$V$
, we obtain a
![]() $\mathop{\textrm{Gal}}\nolimits (\ell )$
-equivariant filtered extension
$\mathop{\textrm{Gal}}\nolimits (\ell )$
-equivariant filtered extension
![]() $\mathcal{P}_{\ast }(\varphi _{\ell }^{\ast }(\mathcal{V}))$
over
$\mathcal{P}_{\ast }(\varphi _{\ell }^{\ast }(\mathcal{V}))$
over
![]() $\mathcal{V}^{(\ell )}$
as follows:
$\mathcal{V}^{(\ell )}$
as follows:
 \begin{align*} \mathcal {P}_a(\varphi _{\ell }^{\ast }\mathcal {V}) =\sum _{\substack {b\in \mathbb {R}, k\in \mathbb {Z}\\[5pt] \ell b+k\leqslant a}} \zeta ^{-k} \varphi _{\ell }^{\ast }(\mathcal {P}_{b}\mathcal {V}) \subset \varphi _{\ell }^{\ast }(\mathcal {V}). \end{align*}
\begin{align*} \mathcal {P}_a(\varphi _{\ell }^{\ast }\mathcal {V}) =\sum _{\substack {b\in \mathbb {R}, k\in \mathbb {Z}\\[5pt] \ell b+k\leqslant a}} \zeta ^{-k} \varphi _{\ell }^{\ast }(\mathcal {P}_{b}\mathcal {V}) \subset \varphi _{\ell }^{\ast }(\mathcal {V}). \end{align*}
The filtered bundle
![]() $\mathcal{P}_{\ast }(\varphi _{\ell }^{\ast }(\mathcal{V}))$
is denoted by
$\mathcal{P}_{\ast }(\varphi _{\ell }^{\ast }(\mathcal{V}))$
is denoted by
![]() $\varphi _{\ell }^{\ast }(\mathcal{P}_{\ast }\mathcal{V})$
.
$\varphi _{\ell }^{\ast }(\mathcal{P}_{\ast }\mathcal{V})$
.
For a
![]() $\mathop{\textrm{Gal}}\nolimits (\ell )$
-equivariant filtered extension
$\mathop{\textrm{Gal}}\nolimits (\ell )$
-equivariant filtered extension
![]() $\mathcal{P}_{\ast }(\mathcal{V}^{(\ell )})$
of
$\mathcal{P}_{\ast }(\mathcal{V}^{(\ell )})$
of
![]() $V^{(\ell )}$
, we obtain a filtered extension
$V^{(\ell )}$
, we obtain a filtered extension
![]() $\mathcal{P}_{\ast }(\varphi _{\ell \ast }(\mathcal{V}^{(\ell )})^{\mathop{\textrm{Gal}}\nolimits (\ell )})$
as follows:
$\mathcal{P}_{\ast }(\varphi _{\ell \ast }(\mathcal{V}^{(\ell )})^{\mathop{\textrm{Gal}}\nolimits (\ell )})$
as follows:
It is called the descent of
![]() $\mathcal{P}_{\ast }(\mathcal{V}^{(\ell )})$
.
$\mathcal{P}_{\ast }(\mathcal{V}^{(\ell )})$
.
Lemma 5.3.
These procedures induce an equivalence between filtered extensions of
![]() $V$
and
$V$
and
![]() $\mathop{\textrm{Gal}}\nolimits (\ell )$
-equivariant filtered extensions of
$\mathop{\textrm{Gal}}\nolimits (\ell )$
-equivariant filtered extensions of
![]() $V^{(\ell )}$
.
$V^{(\ell )}$
.
5.1.2 Non-degenerate symmetric pairing
For any
![]() $b\in \mathbb{R}$
, let
$b\in \mathbb{R}$
, let
![]() $\mathcal{P}^{(b)}_{\ast }(\mathcal{O}_U(\ast 0))$
denote the filtered bundle over
$\mathcal{P}^{(b)}_{\ast }(\mathcal{O}_U(\ast 0))$
denote the filtered bundle over
![]() $\mathcal{O}_U(\ast 0)$
defined by
$\mathcal{O}_U(\ast 0)$
defined by
Here, we set
![]() $[c]:=\max \{n\in \mathbb{Z}\,|\,n\leqslant c\}$
for any
$[c]:=\max \{n\in \mathbb{Z}\,|\,n\leqslant c\}$
for any
![]() $c\in \mathbb{R}$
.
$c\in \mathbb{R}$
.
Let
![]() $C:V\otimes V\to \mathcal{O}_{U^{\ast }}$
be a holomorphic non-degenerate symmetric pairing. We say that a meromorphic extension
$C:V\otimes V\to \mathcal{O}_{U^{\ast }}$
be a holomorphic non-degenerate symmetric pairing. We say that a meromorphic extension
![]() $\mathcal{V}$
is compatible with
$\mathcal{V}$
is compatible with
![]() $C$
if
$C$
if
![]() $C$
extends to a pairing
$C$
extends to a pairing
![]() $\mathcal{V}\otimes \mathcal{V}\to \mathcal{O}_{U}(\ast 0)$
. We say that a filtered extension
$\mathcal{V}\otimes \mathcal{V}\to \mathcal{O}_{U}(\ast 0)$
. We say that a filtered extension
![]() $\mathcal{P}_{\ast }\mathcal{V}$
is compatible with
$\mathcal{P}_{\ast }\mathcal{V}$
is compatible with
![]() $C$
if
$C$
if
![]() $C$
induces
$C$
induces
![]() $\mathcal{P}_{\ast }\mathcal{V}\otimes \mathcal{P}_{\ast }\mathcal{V} \to \mathcal{P}^{(0)}_{\ast }(\mathcal{O}_U(\ast 0))$
. We say that
$\mathcal{P}_{\ast }\mathcal{V}\otimes \mathcal{P}_{\ast }\mathcal{V} \to \mathcal{P}^{(0)}_{\ast }(\mathcal{O}_U(\ast 0))$
. We say that
![]() $C$
is perfect with respect to
$C$
is perfect with respect to
![]() $\mathcal{P}_{\ast }\mathcal{V}$
if
$\mathcal{P}_{\ast }\mathcal{V}$
if
![]() $C$
induces an isomorphism
$C$
induces an isomorphism
![]() $\mathcal{P}_{\ast }(\mathcal{V})\simeq \mathcal{P}_{\ast }(\mathcal{V}^{\lor })$
.
$\mathcal{P}_{\ast }(\mathcal{V})\simeq \mathcal{P}_{\ast }(\mathcal{V}^{\lor })$
.
We have the induced symmetric pairing
![]() $\det (C)$
of
$\det (C)$
of
![]() $\det (V)$
. If
$\det (V)$
. If
![]() $\mathcal{V}$
(respectively
$\mathcal{V}$
(respectively
![]() $\mathcal{P}_{\ast }\mathcal{V}$
) is compatible with
$\mathcal{P}_{\ast }\mathcal{V}$
) is compatible with
![]() $C$
, then
$C$
, then
![]() $\det (\mathcal{V})$
(respectively
$\det (\mathcal{V})$
(respectively
![]() $\det (\mathcal{P}_{\ast }\mathcal{V})$
) is compatible with
$\det (\mathcal{P}_{\ast }\mathcal{V})$
) is compatible with
![]() $\det (C)$
.
$\det (C)$
.
Lemma 5.4 [Reference Li and MochizukiLM10b]. Suppose that
![]() $\mathcal{P}_{\ast }\mathcal{V}$
is compatible with
$\mathcal{P}_{\ast }\mathcal{V}$
is compatible with
![]() $C$
. Then,
$C$
. Then,
![]() $C$
is perfect with respect to
$C$
is perfect with respect to
![]() $\mathcal{P}_{\ast }(\mathcal{V})$
if and only if
$\mathcal{P}_{\ast }(\mathcal{V})$
if and only if
![]() $\det (C)$
is perfect with respect to
$\det (C)$
is perfect with respect to
![]() $\det (\mathcal{P}_{\ast }\mathcal{V})$
.
$\det (\mathcal{P}_{\ast }\mathcal{V})$
.
Lemma 5.5.
There exists a unique meromorphic extension
![]() $\mathcal{L}$
of
$\mathcal{L}$
of
![]() $\det (V)$
which is compatible with
$\det (V)$
which is compatible with
![]() $\det (C)$
. There exists a unique filtered bundle
$\det (C)$
. There exists a unique filtered bundle
![]() $\mathcal{P}^{C}_{\ast }\mathcal{L}$
over
$\mathcal{P}^{C}_{\ast }\mathcal{L}$
over
![]() $\mathcal{L}$
such that
$\mathcal{L}$
such that
![]() $\det (C)$
is perfect with respect to
$\det (C)$
is perfect with respect to
![]() $\mathcal{P}^C_{\ast }\mathcal{L}$
.
$\mathcal{P}^C_{\ast }\mathcal{L}$
.
Proof.
We may assume that
![]() $U$
is a disc. Let
$U$
is a disc. Let
![]() $v_0$
be a frame of
$v_0$
be a frame of
![]() $\det (V)$
on
$\det (V)$
on
![]() $U^{\ast }$
. We obtain a holomorphic function
$U^{\ast }$
. We obtain a holomorphic function
![]() $(\det C)(v_0,v_0)$
on
$(\det C)(v_0,v_0)$
on
![]() $U^{\ast }$
. There exist an integer
$U^{\ast }$
. There exist an integer
![]() $k$
and a holomorphic function
$k$
and a holomorphic function
![]() $g_1$
such that
$g_1$
such that
![]() $(\det C)(v_0,v_0)=z^{-k}\exp (g_1)$
. We obtain a frame
$(\det C)(v_0,v_0)=z^{-k}\exp (g_1)$
. We obtain a frame
![]() $v_1=\exp (-g_1/2)v_0$
of
$v_1=\exp (-g_1/2)v_0$
of
![]() $\det (V)$
on
$\det (V)$
on
![]() $U^{\ast }$
. We set
$U^{\ast }$
. We set
![]() $\mathcal{L}=\mathcal{O}_{U}(\ast 0)v_1 \subset \iota _{\ast }(\det V)$
. Then,
$\mathcal{L}=\mathcal{O}_{U}(\ast 0)v_1 \subset \iota _{\ast }(\det V)$
. Then,
![]() $\mathcal{L}$
is compatible with
$\mathcal{L}$
is compatible with
![]() $\det (C)$
.
$\det (C)$
.
We have
![]() $\det (C)(v_1,v_1)=z^{-k}$
. We define
$\det (C)(v_1,v_1)=z^{-k}$
. We define
Then,
![]() $\mathcal{P}^C_{\ast }\mathcal{L}$
satisfies the desired condition. The uniqueness is clear.
$\mathcal{P}^C_{\ast }\mathcal{L}$
satisfies the desired condition. The uniqueness is clear.
We set
![]() $C^{(\ell )}:=\varphi _{\ell }^{\ast }C$
which is a non-degenerate symmetric pairing of
$C^{(\ell )}:=\varphi _{\ell }^{\ast }C$
which is a non-degenerate symmetric pairing of
![]() $V^{(\ell )}$
.
$V^{(\ell )}$
.
Lemma 5.6.
![]() $\mathcal{V}$
(respectively
$\mathcal{V}$
(respectively
![]() $\mathcal{P}_{\ast }\mathcal{V}$
) is compatible with
$\mathcal{P}_{\ast }\mathcal{V}$
) is compatible with
![]() $C$
if and only if
$C$
if and only if
![]() $\varphi _{\ell }^{\ast }(\mathcal{V})$
(respectively
$\varphi _{\ell }^{\ast }(\mathcal{V})$
(respectively
![]() $\varphi _{\ell }^{\ast }(\mathcal{P}_{\ast }\mathcal{V})$
) is compatible with
$\varphi _{\ell }^{\ast }(\mathcal{P}_{\ast }\mathcal{V})$
) is compatible with
![]() $C^{(\ell )}$
. When
$C^{(\ell )}$
. When
![]() $\mathcal{P}_{\ast }\mathcal{V}$
and
$\mathcal{P}_{\ast }\mathcal{V}$
and
![]() $C$
are compatible,
$C$
are compatible,
![]() $C$
is perfect with respect to
$C$
is perfect with respect to
![]() $\mathcal{P}_{\ast }\mathcal{V}$
if and only if
$\mathcal{P}_{\ast }\mathcal{V}$
if and only if
![]() $C^{(\ell )}$
is perfect with respect to
$C^{(\ell )}$
is perfect with respect to
![]() $\varphi _{\ell }^{\ast }(\mathcal{P}_{\ast }\mathcal{V})$
.
$\varphi _{\ell }^{\ast }(\mathcal{P}_{\ast }\mathcal{V})$
.
5.1.3 Higgs bundles
Let
![]() $\theta$
be a Higgs field of
$\theta$
be a Higgs field of
![]() $V$
, i.e.
$V$
, i.e.
![]() $\theta :V\to V\otimes \Omega ^1_{U^{\ast }}$
. We obtain
$\theta :V\to V\otimes \Omega ^1_{U^{\ast }}$
. We obtain
![]() $\iota _{\ast }(\theta ):\iota _{\ast }(V)\to \iota _{\ast }(V)\otimes \Omega ^1_{U}$
. A meromorphic (respectively smooth) extension of
$\iota _{\ast }(\theta ):\iota _{\ast }(V)\to \iota _{\ast }(V)\otimes \Omega ^1_{U}$
. A meromorphic (respectively smooth) extension of
![]() $(V,\theta )$
is defined to be a meromorphic (respectively smooth) extension
$(V,\theta )$
is defined to be a meromorphic (respectively smooth) extension
![]() $\mathcal{V}$
of
$\mathcal{V}$
of
![]() $V$
such that
$V$
such that
![]() $\iota _{\ast }(\theta )(\mathcal{V})\subset \mathcal{V}\otimes \Omega ^1_U$
. The induced Higgs field of
$\iota _{\ast }(\theta )(\mathcal{V})\subset \mathcal{V}\otimes \Omega ^1_U$
. The induced Higgs field of
![]() $\mathcal{V}$
is denoted by
$\mathcal{V}$
is denoted by
![]() $\theta$
. A filtered extension of
$\theta$
. A filtered extension of
![]() $(V,\theta )$
is defined to be a filtered extension
$(V,\theta )$
is defined to be a filtered extension
![]() $\mathcal{P}_{\ast }(\mathcal{V})$
over a meromorphic extension
$\mathcal{P}_{\ast }(\mathcal{V})$
over a meromorphic extension
![]() $\mathcal{V}$
of
$\mathcal{V}$
of
![]() $(V,\theta )$
. A filtered extension
$(V,\theta )$
. A filtered extension
![]() $(\mathcal{P}_{\ast }\mathcal{V},\theta )$
is said to be regular (respectively good, unramifiedly good) if
$(\mathcal{P}_{\ast }\mathcal{V},\theta )$
is said to be regular (respectively good, unramifiedly good) if
![]() $(\mathcal{P}_{\ast }\mathcal{V},\theta )$
is a regular (respectively good, unramifiedly good) filtered Higgs bundle. (See [Reference MochizukiMoc21, §2.4] for the notion of good filtered Higgs bundles and unramifiedly good filtered Higgs bundles.)
$(\mathcal{P}_{\ast }\mathcal{V},\theta )$
is a regular (respectively good, unramifiedly good) filtered Higgs bundle. (See [Reference MochizukiMoc21, §2.4] for the notion of good filtered Higgs bundles and unramifiedly good filtered Higgs bundles.)
Lemma 5.7.
Let
![]() $f$
be the endomorphism of
$f$
be the endomorphism of
![]() $V$
defined by
$V$
defined by
![]() $\theta =f\,dz/z$
. Let
$\theta =f\,dz/z$
. Let
![]() $a_j(z)$
be the holomorphic functions on
$a_j(z)$
be the holomorphic functions on
![]() $U^{\ast }$
obtained as the coefficients of the characteristic polynomial
$U^{\ast }$
obtained as the coefficients of the characteristic polynomial
![]() $\det (t{\mathop{\textrm{id}}\nolimits }_V-f)=\sum _{j=0}^r a_j(z)t^j$
.
$\det (t{\mathop{\textrm{id}}\nolimits }_V-f)=\sum _{j=0}^r a_j(z)t^j$
.
-
– A meromorphic extension of
 $(V,\theta )$
exists if and only if the Higgs bundle
$(V,\theta )$
exists if and only if the Higgs bundle
 $(V,\theta )$
is wild, i.e.
$(V,\theta )$
is wild, i.e.
 $a_j(z)$
are meromorphic at
$a_j(z)$
are meromorphic at
 $z=0$
. In that case, there exists a good filtered extension.
$z=0$
. In that case, there exists a good filtered extension.
-
– A regular filtered extension exists if and only if
 $(V,\theta )$
is tame, i.e.
$(V,\theta )$
is tame, i.e.
 $a_j(z)$
are holomorphic at
$a_j(z)$
are holomorphic at
 $z=0$
.
$z=0$
.
We obtain the Higgs field
![]() $\theta ^{(\ell )}$
of
$\theta ^{(\ell )}$
of
![]() $V^{(\ell )}$
. The following lemmas are clear.
$V^{(\ell )}$
. The following lemmas are clear.
Lemma 5.8.
The pull back and the descent induce an equivalence between meromorphic extensions of
![]() $(V,\theta )$
and
$(V,\theta )$
and
![]() $\mathop{\textrm{Gal}}\nolimits (\ell )$
-equivariant meromorphic extensions of
$\mathop{\textrm{Gal}}\nolimits (\ell )$
-equivariant meromorphic extensions of
![]() $(V^{(\ell )},\theta ^{(\ell )})$
.
$(V^{(\ell )},\theta ^{(\ell )})$
.
Lemma 5.9.
The pull back and the descent induce an equivalence between regular (respectively good) filtered extensions of
![]() $(V,\theta )$
and
$(V,\theta )$
and
![]() $\mathop{\textrm{Gal}}\nolimits (\ell )$
-equivariant regular (respectively good) filtered meromorphic extensions of
$\mathop{\textrm{Gal}}\nolimits (\ell )$
-equivariant regular (respectively good) filtered meromorphic extensions of
![]() $(V^{(\ell )},\theta ^{(\ell )})$
.
$(V^{(\ell )},\theta ^{(\ell )})$
.
5.2 Decomposable filtered extensions of regular semisimple Higgs bundles
5.2.1 Decomposable filtered extensions
We continue to use the notation in §5.1.1. Let
![]() $(V,\theta )$
be a regular semisimple Higgs bundle on
$(V,\theta )$
be a regular semisimple Higgs bundle on
![]() $U^{\ast }$
. Assume that
$U^{\ast }$
. Assume that
![]() $\theta$
is wild. There exist
$\theta$
is wild. There exist
![]() $\ell \in \mathbb{Z}_{\gt 0}$
and the decomposition
$\ell \in \mathbb{Z}_{\gt 0}$
and the decomposition
 \begin{align} \varphi _{\ell }^{\ast }(V,\theta ) =\bigoplus _{i=1}^r (V_i,\theta _i), \end{align}
\begin{align} \varphi _{\ell }^{\ast }(V,\theta ) =\bigoplus _{i=1}^r (V_i,\theta _i), \end{align}
where
![]() $\mathop{\textrm{rank}}\nolimits V_i=1$
, and
$\mathop{\textrm{rank}}\nolimits V_i=1$
, and
![]() $\theta _i-\theta _j$
$\theta _i-\theta _j$
![]() $(i\neq j)$
are nowhere vanishing on
$(i\neq j)$
are nowhere vanishing on
![]() $U^{(\ell )\ast }$
. Let
$U^{(\ell )\ast }$
. Let
![]() $\mathcal{V}$
be a meromorphic extension of
$\mathcal{V}$
be a meromorphic extension of
![]() $(V,\theta )$
. The decomposition (34) extends to
$(V,\theta )$
. The decomposition (34) extends to
 \begin{align} \varphi _{\ell }^{\ast }(\mathcal{V},\theta ) =\bigoplus _{i=1}^r (\mathcal{V}_i,\theta _i), \end{align}
\begin{align} \varphi _{\ell }^{\ast }(\mathcal{V},\theta ) =\bigoplus _{i=1}^r (\mathcal{V}_i,\theta _i), \end{align}
where each
![]() $\mathcal{V}_i$
is a meromorphic extension of
$\mathcal{V}_i$
is a meromorphic extension of
![]() $V_i$
.
$V_i$
.
Definition 5.10. A filtered bundle
![]() $\mathcal{P}_{\ast }\mathcal{V}$
over
$\mathcal{P}_{\ast }\mathcal{V}$
over
![]() $\mathcal{V}$
is called a decomposable filtered extension of
$\mathcal{V}$
is called a decomposable filtered extension of
![]() $(V,\theta )$
if the filtered bundle
$(V,\theta )$
if the filtered bundle
![]() $\varphi _{\ell }^{\ast }(\mathcal{P}_{\ast }\mathcal{V})$
is compatible with the decomposition (35), i.e. the following holds for any
$\varphi _{\ell }^{\ast }(\mathcal{P}_{\ast }\mathcal{V})$
is compatible with the decomposition (35), i.e. the following holds for any
![]() $a\in \mathbb{R}$
:
$a\in \mathbb{R}$
:
 \begin{align*} \mathcal {P}_{a}(\varphi _{\ell }^{\ast }\mathcal {V}) =\bigoplus _{i=1}^r \mathcal {P}_a(\varphi _{\ell }^{\ast }\mathcal {V}) \cap \mathcal {V}_{i}. \end{align*}
\begin{align*} \mathcal {P}_{a}(\varphi _{\ell }^{\ast }\mathcal {V}) =\bigoplus _{i=1}^r \mathcal {P}_a(\varphi _{\ell }^{\ast }\mathcal {V}) \cap \mathcal {V}_{i}. \end{align*}
Such a
![]() $(\mathcal{P}_{\ast }\mathcal{V},\theta )$
is called a decomposable filtered Higgs bundle.
$(\mathcal{P}_{\ast }\mathcal{V},\theta )$
is called a decomposable filtered Higgs bundle.
The following lemma is obvious by definition.
Lemma 5.11.
Suppose that
![]() $(\mathcal{P}_{\ast }\mathcal{V},\theta )$
is decomposable:
$(\mathcal{P}_{\ast }\mathcal{V},\theta )$
is decomposable:
-
–
 $(\mathcal{P}_{\ast }\mathcal{V},\theta )$
is a good filtered Higgs bundle;
$(\mathcal{P}_{\ast }\mathcal{V},\theta )$
is a good filtered Higgs bundle;
-
– any decomposition
 $(\mathcal{V},\theta )_{|U^{\ast }} =(V_1,\theta _1)\oplus (V_2,\theta _2)$
extends to a decomposition
$(\mathcal{V},\theta )_{|U^{\ast }} =(V_1,\theta _1)\oplus (V_2,\theta _2)$
extends to a decomposition
 $(\mathcal{P}_{\ast }\mathcal{V},\theta ) =(\mathcal{P}_{\ast }\mathcal{V}_1,\theta _1)\oplus (\mathcal{P}_{\ast }\mathcal{V}_2,\theta _2)$
such that
$(\mathcal{P}_{\ast }\mathcal{V},\theta ) =(\mathcal{P}_{\ast }\mathcal{V}_1,\theta _1)\oplus (\mathcal{P}_{\ast }\mathcal{V}_2,\theta _2)$
such that
 $\mathcal{V}_{i|U^{\ast }}=V_i$
.
$\mathcal{V}_{i|U^{\ast }}=V_i$
.
5.2.2 Filtered line bundles and decomposable filtered Higgs bundles
There exists the decomposition
such that
![]() $\Sigma _{V^{[k]},\theta ^{[k]}}$
are connected. We set
$\Sigma _{V^{[k]},\theta ^{[k]}}$
are connected. We set
![]() $r_k=\mathop{\textrm{rank}}\nolimits V^{[k]}$
. For each
$r_k=\mathop{\textrm{rank}}\nolimits V^{[k]}$
. For each
![]() $k$
, there exists the decomposition of the Higgs bundle
$k$
, there exists the decomposition of the Higgs bundle
 \begin{align} \varphi _{r_k}^{\ast }(V^{[k]},\theta ^{[k]}) =\bigoplus _{i=1}^{r_k} (V^{[k]}_i,\theta ^{[k]}_i), \end{align}
\begin{align} \varphi _{r_k}^{\ast }(V^{[k]},\theta ^{[k]}) =\bigoplus _{i=1}^{r_k} (V^{[k]}_i,\theta ^{[k]}_i), \end{align}
where
![]() $\mathop{\textrm{rank}}\nolimits V^{[k]}_i=1$
, and
$\mathop{\textrm{rank}}\nolimits V^{[k]}_i=1$
, and
![]() $\theta ^{[k]}_i$
are
$\theta ^{[k]}_i$
are
![]() $1$
-forms such that
$1$
-forms such that
![]() $\theta ^{[k]}_i-\theta ^{[k]}_j$
$\theta ^{[k]}_i-\theta ^{[k]}_j$
![]() $(i\neq j)$
are nowhere vanishing on
$(i\neq j)$
are nowhere vanishing on
![]() $U^{(r_k)\ast }$
. A decomposable filtered extension
$U^{(r_k)\ast }$
. A decomposable filtered extension
![]() $\mathcal{P}_{\ast }\mathcal{V}$
of
$\mathcal{P}_{\ast }\mathcal{V}$
of
![]() $(V,\theta )$
induces filtered extensions
$(V,\theta )$
induces filtered extensions
![]() $\mathcal{P}_{\ast }(\mathcal{V}^{[k]}_i)$
of
$\mathcal{P}_{\ast }(\mathcal{V}^{[k]}_i)$
of
![]() $(V^{[k]}_i,\theta ^{[k]}_i)$
. Note that
$(V^{[k]}_i,\theta ^{[k]}_i)$
. Note that
![]() $\mathcal{P}_{\ast }(\mathcal{V}^{[k]}_i) =\sigma ^{\ast }\mathcal{P}_{\ast }(\mathcal{V}^{[k]}_1)$
for
$\mathcal{P}_{\ast }(\mathcal{V}^{[k]}_i) =\sigma ^{\ast }\mathcal{P}_{\ast }(\mathcal{V}^{[k]}_1)$
for
![]() $\sigma \in \mathop{\textrm{Gal}}\nolimits (r_k)$
such that
$\sigma \in \mathop{\textrm{Gal}}\nolimits (r_k)$
such that
![]() $\sigma ^{\ast }\theta ^{[k]}_1=\theta ^{[k]}_i$
. Conversely, a filtered extension
$\sigma ^{\ast }\theta ^{[k]}_1=\theta ^{[k]}_i$
. Conversely, a filtered extension
![]() $\mathcal{P}_{\ast }\mathcal{V}^{[k]}_1$
of
$\mathcal{P}_{\ast }\mathcal{V}^{[k]}_1$
of
![]() $V^{[k]}_1$
induces a
$V^{[k]}_1$
induces a
![]() $\mathop{\textrm{Gal}}\nolimits (r_k)$
-equivariant filtered extension
$\mathop{\textrm{Gal}}\nolimits (r_k)$
-equivariant filtered extension
![]() $\bigoplus _{\sigma \in \mathop{\textrm{Gal}}\nolimits (r_k)} \sigma ^{\ast }\mathcal{P}_{\ast }\mathcal{V}^{[k]}_1$
of
$\bigoplus _{\sigma \in \mathop{\textrm{Gal}}\nolimits (r_k)} \sigma ^{\ast }\mathcal{P}_{\ast }\mathcal{V}^{[k]}_1$
of
![]() $\varphi _{r_k}^{\ast }(V^{[k]})=\bigoplus _{i=1}^{r_k} V^{[k]}_i$
, and hence a decomposable filtered extension
$\varphi _{r_k}^{\ast }(V^{[k]})=\bigoplus _{i=1}^{r_k} V^{[k]}_i$
, and hence a decomposable filtered extension
![]() $\mathcal{P}_{\ast }\mathcal{V}^{[k]}$
of
$\mathcal{P}_{\ast }\mathcal{V}^{[k]}$
of
![]() $(V^{[k]},\theta ^{[k]})$
. Thus, we obtain a decomposable filtered extension
$(V^{[k]},\theta ^{[k]})$
. Thus, we obtain a decomposable filtered extension
![]() $\bigoplus _{k\in S}\mathcal{P}_{\ast }\mathcal{V}^{[k]}$
of
$\bigoplus _{k\in S}\mathcal{P}_{\ast }\mathcal{V}^{[k]}$
of
![]() $(V,\theta )$
. Note that
$(V,\theta )$
. Note that
![]() $\mathcal{P}_{\ast }\mathcal{V}^{[k]}$
is also obtained as
$\mathcal{P}_{\ast }\mathcal{V}^{[k]}$
is also obtained as
![]() $(\varphi _{r_k})_{\ast }(\mathcal{P}_{\ast }\mathcal{V}^{[k]}_1)$
by the natural identification
$(\varphi _{r_k})_{\ast }(\mathcal{P}_{\ast }\mathcal{V}^{[k]}_1)$
by the natural identification
![]() $(\varphi _{r_k})_{\ast }(V^{[k]}_1)=V^{[k]}$
. The following proposition is easy to see.
$(\varphi _{r_k})_{\ast }(V^{[k]}_1)=V^{[k]}$
. The following proposition is easy to see.
Proposition 5.12.
This procedure induces an equivalence between decomposable filtered extensions of
![]() $(V,\theta )$
and a tuple of filtered extensions of
$(V,\theta )$
and a tuple of filtered extensions of
![]() $V^{[k]}_1$
$V^{[k]}_1$
![]() $(k\in S)$
.
$(k\in S)$
.
5.2.3 Decomposable filtered extension determined by determinant bundles
Let
![]() $\mathcal{V}$
be a meromorphic extension of
$\mathcal{V}$
be a meromorphic extension of
![]() $(V,\theta )$
. The decomposition (36) extends to a decomposition
$(V,\theta )$
. The decomposition (36) extends to a decomposition
The decomposition (35) extends to a decomposition
 \begin{align} \varphi _{r_k}^{\ast }(\mathcal{V}^{[k]},\theta ^{[k]}) =\bigoplus _{i=1}^{r_k} (\mathcal{V}^{[k]}_i,\theta ^{[k]}_i). \end{align}
\begin{align} \varphi _{r_k}^{\ast }(\mathcal{V}^{[k]},\theta ^{[k]}) =\bigoplus _{i=1}^{r_k} (\mathcal{V}^{[k]}_i,\theta ^{[k]}_i). \end{align}
Proposition 5.13.
For a tuple of filtered bundles
![]() $\mathcal{P}_{\ast }\det (\mathcal{V}^{[k]})$
over
$\mathcal{P}_{\ast }\det (\mathcal{V}^{[k]})$
over
![]() $\det (\mathcal{V}^{[k]})$
, there uniquely exists a decomposable filtered bundle
$\det (\mathcal{V}^{[k]})$
, there uniquely exists a decomposable filtered bundle
![]() $\mathcal{P}^{\star }_{\ast }(\mathcal{V}) =\bigoplus _{k\in S}\mathcal{P}^{\star }_{\ast }(\mathcal{V}^{[k]})$
over
$\mathcal{P}^{\star }_{\ast }(\mathcal{V}) =\bigoplus _{k\in S}\mathcal{P}^{\star }_{\ast }(\mathcal{V}^{[k]})$
over
![]() $\mathcal{V}$
such that
$\mathcal{V}$
such that
![]() $\det (\mathcal{P}^{\star }_{\ast }\mathcal{V}^{[k]}) =\mathcal{P}_{\ast }\det (\mathcal{V}^{[k]})$
for any
$\det (\mathcal{P}^{\star }_{\ast }\mathcal{V}^{[k]}) =\mathcal{P}_{\ast }\det (\mathcal{V}^{[k]})$
for any
![]() $k\in S$
. Moreover, the following hold for any
$k\in S$
. Moreover, the following hold for any
![]() $k\in S$
:
$k\in S$
:
-
–
 $\dim \mathop{\textrm{Gr}}\nolimits ^{\mathcal{P}^{\star }}_a(\mathcal{V}^{[k]})\leqslant 1$
for any
$\dim \mathop{\textrm{Gr}}\nolimits ^{\mathcal{P}^{\star }}_a(\mathcal{V}^{[k]})\leqslant 1$
for any
 $a\in \mathbb{R}$
;
$a\in \mathbb{R}$
; -
– let
 $d_k$
be a real number such that
$d_k$
be a real number such that
 $\mathop{\textrm{Gr}}\nolimits ^{\mathcal{P}}_{d_k}(\det (\mathcal{V}^{[k]}))\neq 0$
, so then
$\mathop{\textrm{Gr}}\nolimits ^{\mathcal{P}}_{d_k}(\det (\mathcal{V}^{[k]}))\neq 0$
, so then
 $\mathop{\textrm{Gr}}\nolimits ^{\mathcal{P}^{\star }}_{a}(\mathcal{V}^{[k]})\neq 0$
if and only if
$\mathop{\textrm{Gr}}\nolimits ^{\mathcal{P}^{\star }}_{a}(\mathcal{V}^{[k]})\neq 0$
if and only if
 $r_ka-d_k\in \mathbb{Z}$
(
$r_ka-d_k\in \mathbb{Z}$
(
 $r_k$
is odd) or
$r_k$
is odd) or
 $r_ka-d_k\in {1 \over 2}\mathbb{Z}\setminus \mathbb{Z}$
(
$r_ka-d_k\in {1 \over 2}\mathbb{Z}\setminus \mathbb{Z}$
(
 $r_k$
is even).
$r_k$
is even).
-
–
 $\mathop{\textrm{Gr}}\nolimits ^{\mathcal{P}^{\star }}_a(\mathcal{V}^{[k]}_i)\neq 0$
if and only if
$\mathop{\textrm{Gr}}\nolimits ^{\mathcal{P}^{\star }}_a(\mathcal{V}^{[k]}_i)\neq 0$
if and only if
 $a-d_k\in \mathbb{Z}$
(
$a-d_k\in \mathbb{Z}$
(
 $r_k$
is odd) or
$r_k$
is odd) or
 $a-d_k\in {1 \over 2}\mathbb{Z}$
(
$a-d_k\in {1 \over 2}\mathbb{Z}$
(
 $r_k$
is even).
$r_k$
is even).
Proof.
It is enough to consider the case where
![]() $\Sigma _{V,\theta }$
is connected, i.e.
$\Sigma _{V,\theta }$
is connected, i.e.
![]() $|S|=1$
. We omit the superscript
$|S|=1$
. We omit the superscript
![]() $[k]$
and the subscript
$[k]$
and the subscript
![]() $k$
. We set
$k$
. We set
![]() $(V^{(r)},\theta ^{(r)})=\varphi _r^{\ast }(V,\theta )$
and
$(V^{(r)},\theta ^{(r)})=\varphi _r^{\ast }(V,\theta )$
and
![]() $\mathcal{V}^{(r)}=\varphi _{r}^{\ast }(\mathcal{V})$
. There exists the following decomposition of the Higgs bundle on
$\mathcal{V}^{(r)}=\varphi _{r}^{\ast }(\mathcal{V})$
. There exists the following decomposition of the Higgs bundle on
![]() $U^{(r)\ast }$
:
$U^{(r)\ast }$
:
 \begin{align} (V^{(r)},\theta ^{(r)}) =\bigoplus _{i=1}^r (V_{\beta (i)},\beta (i)\,d\zeta ). \end{align}
\begin{align} (V^{(r)},\theta ^{(r)}) =\bigoplus _{i=1}^r (V_{\beta (i)},\beta (i)\,d\zeta ). \end{align}
Here,
![]() $\beta (i)$
are meromorphic functions on
$\beta (i)$
are meromorphic functions on
![]() $(U^{(r)},0)$
such that
$(U^{(r)},0)$
such that
![]() $\beta (i)-\beta (j)$
$\beta (i)-\beta (j)$
![]() $(i\neq j)$
are nowhere vanishing on
$(i\neq j)$
are nowhere vanishing on
![]() $U^{(r)\ast }$
. The decomposition (40) extends to a decomposition on
$U^{(r)\ast }$
. The decomposition (40) extends to a decomposition on
![]() $U^{(r)}$
:
$U^{(r)}$
:
 \begin{align} (\mathcal{V}^{(r)},\theta ^{(r)}) =\bigoplus _{i=1}^{r} (\mathcal{V}_{\beta (i)},\beta (i)\,d\zeta ). \end{align}
\begin{align} (\mathcal{V}^{(r)},\theta ^{(r)}) =\bigoplus _{i=1}^{r} (\mathcal{V}_{\beta (i)},\beta (i)\,d\zeta ). \end{align}
We have
![]() $\sigma ^{\ast }\mathcal{V}_{\beta (i)} =\mathcal{V}_{\sigma ^{\ast }(\beta (i))}$
for any
$\sigma ^{\ast }\mathcal{V}_{\beta (i)} =\mathcal{V}_{\sigma ^{\ast }(\beta (i))}$
for any
![]() $\sigma \in \mathop{\textrm{Gal}}\nolimits (r)$
.
$\sigma \in \mathop{\textrm{Gal}}\nolimits (r)$
.
Let
![]() $v_{\beta (1)}$
be a frame of
$v_{\beta (1)}$
be a frame of
![]() $\mathcal{V}_{\beta (1)}$
. We obtain frames
$\mathcal{V}_{\beta (1)}$
. We obtain frames
![]() $v_{\sigma ^{\ast }(\beta (1))}=\sigma ^{\ast }v_{\beta (1)}$
of
$v_{\sigma ^{\ast }(\beta (1))}=\sigma ^{\ast }v_{\beta (1)}$
of
![]() $\mathcal{V}_{\sigma ^{\ast }\beta (1)}$
, and the tuple
$\mathcal{V}_{\sigma ^{\ast }\beta (1)}$
, and the tuple
![]() $v_{\beta (1)},\ldots, v_{\beta (r)}$
is a frame of
$v_{\beta (1)},\ldots, v_{\beta (r)}$
is a frame of
![]() $\mathcal{V}^{(r)}$
. We set
$\mathcal{V}^{(r)}$
. We set
We define the filtered bundles
![]() $\mathcal{P}^{\star }_{\ast }(\mathcal{V}_{\beta (i)})$
as follows:
$\mathcal{P}^{\star }_{\ast }(\mathcal{V}_{\beta (i)})$
as follows:
They are independent of the choice of
![]() $v_{\beta (1)}$
. We set
$v_{\beta (1)}$
. We set
![]() $\mathcal{P}^{\star }_{\ast }(\mathcal{V}^{(r)}) =\bigoplus \mathcal{P}^{\star }_{\ast }(\mathcal{V}_{\beta (i)})$
, which is
$\mathcal{P}^{\star }_{\ast }(\mathcal{V}^{(r)}) =\bigoplus \mathcal{P}^{\star }_{\ast }(\mathcal{V}_{\beta (i)})$
, which is
![]() $\mathop{\textrm{Gal}}\nolimits (r)$
-equivariant. As the descent, we obtain a filtered bundle
$\mathop{\textrm{Gal}}\nolimits (r)$
-equivariant. As the descent, we obtain a filtered bundle
![]() $\mathcal{P}^{\star }_{\ast }(\mathcal{V})$
over
$\mathcal{P}^{\star }_{\ast }(\mathcal{V})$
over
![]() $\mathcal{V}$
, which satisfies the desired condition. The uniqueness is clear. By the construction,
$\mathcal{V}$
, which satisfies the desired condition. The uniqueness is clear. By the construction,
![]() $(\mathcal{P}^{\star }_{\ast }(\mathcal{V}),\theta )$
is clearly a good filtered Higgs bundle.
$(\mathcal{P}^{\star }_{\ast }(\mathcal{V}),\theta )$
is clearly a good filtered Higgs bundle.
Let
![]() $\tau$
be a frame of
$\tau$
be a frame of
![]() $\mathcal{P}_d(\det \mathcal{V})$
. There exist an integer
$\mathcal{P}_d(\det \mathcal{V})$
. There exist an integer
![]() $m$
and a nowhere vanishing holomorphic function
$m$
and a nowhere vanishing holomorphic function
![]() $g$
on
$g$
on
![]() $U^{(r)}$
such that
$U^{(r)}$
such that
Because a generator
![]() $\sigma _0$
of
$\sigma _0$
of
![]() $\mathop{\textrm{Gal}}\nolimits (r)$
acts on the set
$\mathop{\textrm{Gal}}\nolimits (r)$
acts on the set
![]() $\{\beta (i)\}$
in a cyclic way, we have
$\{\beta (i)\}$
in a cyclic way, we have
![]() $\sigma _0^{\ast }(v_{\beta (1)}\wedge \cdots \wedge v_{\beta (r)}) =(-1)^{(r-1)}v_{\beta (1)}\wedge \cdots \wedge v_{\beta (r)}$
. Hence, we obtain that
$\sigma _0^{\ast }(v_{\beta (1)}\wedge \cdots \wedge v_{\beta (r)}) =(-1)^{(r-1)}v_{\beta (1)}\wedge \cdots \wedge v_{\beta (r)}$
. Hence, we obtain that
![]() $\sigma _0^{\ast }(\zeta ^m)=(-1)^{r-1}\zeta ^m$
and
$\sigma _0^{\ast }(\zeta ^m)=(-1)^{r-1}\zeta ^m$
and
![]() $\sigma _0^{\ast }g=g$
. This implies that
$\sigma _0^{\ast }g=g$
. This implies that
![]() $m/r\in \mathbb{Z}$
if
$m/r\in \mathbb{Z}$
if
![]() $r$
is odd or that
$r$
is odd or that
![]() $m/r\in {1 \over 2}\mathbb{Z}\setminus \mathbb{Z}$
if
$m/r\in {1 \over 2}\mathbb{Z}\setminus \mathbb{Z}$
if
![]() $r$
is even. By our choice of
$r$
is even. By our choice of
![]() $b$
, we have
$b$
, we have
![]() $b=-m+rd$
. It is easy to see that
$b=-m+rd$
. It is easy to see that
![]() $\mathop{\textrm{Gr}}\nolimits ^{\mathcal{P}^{\star }}_c(\mathcal{V}_{\beta (i)})\neq 0$
if and only if
$\mathop{\textrm{Gr}}\nolimits ^{\mathcal{P}^{\star }}_c(\mathcal{V}_{\beta (i)})\neq 0$
if and only if
![]() $c-b/r\in \mathbb{Z}$
. For each
$c-b/r\in \mathbb{Z}$
. For each
![]() $p\in \mathbb{Z}$
, we have the
$p\in \mathbb{Z}$
, we have the
![]() $\mathop{\textrm{Gal}}\nolimits (r)$
-invariant sections
$\mathop{\textrm{Gal}}\nolimits (r)$
-invariant sections
![]() $\sum _{\sigma \in \mathop{\textrm{Gal}}\nolimits (r)} \sigma ^{\ast }(\zeta ^pv_{\beta (1)})$
of
$\sum _{\sigma \in \mathop{\textrm{Gal}}\nolimits (r)} \sigma ^{\ast }(\zeta ^pv_{\beta (1)})$
of
![]() $\mathcal{V}^{(r)}$
which induces a section of
$\mathcal{V}^{(r)}$
which induces a section of
![]() $\mathcal{P}^{\star }_{b/r^2-p/r}(\mathcal{V})$
. Moreover, it induces a frame of
$\mathcal{P}^{\star }_{b/r^2-p/r}(\mathcal{V})$
. Moreover, it induces a frame of
![]() $\mathop{\textrm{Gr}}\nolimits ^{\mathcal{P}^{\star }}_{b/r^2-p/r}(\mathcal{V})$
. Hence, it is easy to see that
$\mathop{\textrm{Gr}}\nolimits ^{\mathcal{P}^{\star }}_{b/r^2-p/r}(\mathcal{V})$
. Hence, it is easy to see that
![]() $\mathop{\textrm{Gr}}\nolimits ^{\mathcal{P}^{\star }}_a(\mathcal{V})\neq 0$
if and only if
$\mathop{\textrm{Gr}}\nolimits ^{\mathcal{P}^{\star }}_a(\mathcal{V})\neq 0$
if and only if
![]() $ra-b/r\in \mathbb{Z}$
, and that
$ra-b/r\in \mathbb{Z}$
, and that
![]() $\dim \mathop{\textrm{Gr}}\nolimits ^{\mathcal{P}^{\star }}_a(\mathcal{V})\leqslant 1$
. Then, we obtain the last two claims.
$\dim \mathop{\textrm{Gr}}\nolimits ^{\mathcal{P}^{\star }}_a(\mathcal{V})\leqslant 1$
. Then, we obtain the last two claims.
5.3 Non-degenerate pairings and decomposable filtered extensions
5.3.1 Non-degenerate symmetric pairings of regular semisimple Higgs bundles
We continue to use the notation in §5.2. Let
![]() $C$
be a non-degenerate symmetric pairing of
$C$
be a non-degenerate symmetric pairing of
![]() $(V,\theta )$
. For any
$(V,\theta )$
. For any
![]() $z_0\in U^{\ast }$
, the eigen decomposition of
$z_0\in U^{\ast }$
, the eigen decomposition of
![]() $\theta$
at
$\theta$
at
![]() $z_0$
is orthogonal with respect to
$z_0$
is orthogonal with respect to
![]() $C$
. The decomposition (34) is orthogonal with respect to
$C$
. The decomposition (34) is orthogonal with respect to
![]() $\varphi _{\ell }^{\ast }C$
.
$\varphi _{\ell }^{\ast }C$
.
The decomposition (36) is orthogonal with respect to
![]() $C$
. Let
$C$
. Let
![]() $C^{[k]}$
denote the restriction of
$C^{[k]}$
denote the restriction of
![]() $C$
to
$C$
to
![]() $V^{[k]}$
. The decomposition (37) is orthogonal with respect to
$V^{[k]}$
. The decomposition (37) is orthogonal with respect to
![]() $\varphi _{r_k}^{\ast }C^{[k]}$
. Let
$\varphi _{r_k}^{\ast }C^{[k]}$
. Let
![]() $C^{[k]}_i$
denote the induced symmetric pairing of
$C^{[k]}_i$
denote the induced symmetric pairing of
![]() $V^{[k]}_i$
. We have
$V^{[k]}_i$
. We have
![]() $C^{[k]}_i=\sigma ^{\ast }C^{[k]}_1$
for
$C^{[k]}_i=\sigma ^{\ast }C^{[k]}_1$
for
![]() $\sigma \in \mathop{\textrm{Gal}}\nolimits (r_k)$
such that
$\sigma \in \mathop{\textrm{Gal}}\nolimits (r_k)$
such that
![]() $\sigma ^{\ast }\theta ^{[k]}_1=\theta ^{[k]}_i$
. Conversely, for any non-degenerate symmetric pairings
$\sigma ^{\ast }\theta ^{[k]}_1=\theta ^{[k]}_i$
. Conversely, for any non-degenerate symmetric pairings
![]() $C^{[k]}_1$
$C^{[k]}_1$
![]() $(k\in S)$
, we obtain a
$(k\in S)$
, we obtain a
![]() $\mathop{\textrm{Gal}}\nolimits (r_k)$
-equivariant non-degenerate symmetric pairing
$\mathop{\textrm{Gal}}\nolimits (r_k)$
-equivariant non-degenerate symmetric pairing
![]() $\bigoplus _{\sigma \in \mathop{\textrm{Gal}}\nolimits (r_k)} \sigma ^{\ast }C^{[k]}_1$
of
$\bigoplus _{\sigma \in \mathop{\textrm{Gal}}\nolimits (r_k)} \sigma ^{\ast }C^{[k]}_1$
of
![]() $\varphi _{r_k}^{\ast }V^{[k]}$
. It induces a non-degenerate symmetric pairing
$\varphi _{r_k}^{\ast }V^{[k]}$
. It induces a non-degenerate symmetric pairing
![]() $C^{[k]}$
of
$C^{[k]}$
of
![]() $(V^{[k]},\theta ^{[k]})$
, and a non-degenerate pairing
$(V^{[k]},\theta ^{[k]})$
, and a non-degenerate pairing
![]() $\bigoplus C^{[k]}$
of
$\bigoplus C^{[k]}$
of
![]() $(V,\theta )$
. The following lemma is a special case of Proposition 2.5.
$(V,\theta )$
. The following lemma is a special case of Proposition 2.5.
Lemma 5.14.
These procedures induce an equivalence between a non-degenerate symmetric pairing
![]() $C$
of
$C$
of
![]() $(V,\theta )$
and a tuple
$(V,\theta )$
and a tuple
![]() $(C^{[k]}_1)_{k\in S}$
of non-degenerate symmetric pairings of
$(C^{[k]}_1)_{k\in S}$
of non-degenerate symmetric pairings of
![]() $V^{[k]}_1$
.
$V^{[k]}_1$
.
5.3.2 Canonical decomposable filtered extensions in the symmetric case
We recall the following [Reference Li and MochizukiLM10b, §4.1].
Proposition 5.15.
For a non-degenerate symmetric pairing
![]() $C$
of
$C$
of
![]() $(V,\theta )$
, there uniquely exists a meromorphic extension
$(V,\theta )$
, there uniquely exists a meromorphic extension
![]() $\mathcal{V}^C$
of
$\mathcal{V}^C$
of
![]() $(V,\theta )$
compatible with
$(V,\theta )$
compatible with
![]() $C$
. Moreover, there uniquely exists a filtered bundle
$C$
. Moreover, there uniquely exists a filtered bundle
![]() $\mathcal{P}^C_{\ast }(\mathcal{V}^C)$
over
$\mathcal{P}^C_{\ast }(\mathcal{V}^C)$
over
![]() $\mathcal{V}^C$
satisfying the following conditions:
$\mathcal{V}^C$
satisfying the following conditions:
-
–
 $C$
is perfect with respect to
$C$
is perfect with respect to
 $\mathcal{P}^C_{\ast }(\mathcal{V}^C)$
;
$\mathcal{P}^C_{\ast }(\mathcal{V}^C)$
; -
–
 $\mathcal{P}^C_{\ast }(\mathcal{V}^C)$
is a decomposable filtered extension of
$\mathcal{P}^C_{\ast }(\mathcal{V}^C)$
is a decomposable filtered extension of
 $(V,\theta )$
.
$(V,\theta )$
.
We have the non-degenerate symmetric pairing
![]() $C^{[k]}_1$
$C^{[k]}_1$
![]() $(k\in S)$
of
$(k\in S)$
of
![]() $V^{[k]}_1$
corresponding to
$V^{[k]}_1$
corresponding to
![]() $C$
as in Lemma 5.14. There exist unique filtered extensions
$C$
as in Lemma 5.14. There exist unique filtered extensions
![]() $\mathcal{P}^C_{\ast }\bigl ((\mathcal{V}^{[k]}_1)^C\bigr )$
of
$\mathcal{P}^C_{\ast }\bigl ((\mathcal{V}^{[k]}_1)^C\bigr )$
of
![]() $V^{[k]}_1$
compatible with
$V^{[k]}_1$
compatible with
![]() $C^{[k]}_1$
as in Lemma 5.5. The decomposable filtered extension
$C^{[k]}_1$
as in Lemma 5.5. The decomposable filtered extension
![]() $\mathcal{P}^C_{\ast }(\mathcal{V}^C)$
of
$\mathcal{P}^C_{\ast }(\mathcal{V}^C)$
of
![]() $(V,\theta )$
corresponds to the tuple
$(V,\theta )$
corresponds to the tuple
![]() $\mathcal{P}^C_{\ast }\bigl ((\mathcal{V}^{[k]}_1)^C\bigr )$
$\mathcal{P}^C_{\ast }\bigl ((\mathcal{V}^{[k]}_1)^C\bigr )$
![]() $(k\in S)$
(Proposition 5.12).
$(k\in S)$
(Proposition 5.12).
5.3.3 Comparison of two canonical extensions
Let
![]() $C$
be a non-degenerate symmetric pairing of
$C$
be a non-degenerate symmetric pairing of
![]() $(V,\theta )$
. We have the unique filtered extension
$(V,\theta )$
. We have the unique filtered extension
![]() $\mathcal{P}^C_{\ast }\mathcal{V}^C$
of
$\mathcal{P}^C_{\ast }\mathcal{V}^C$
of
![]() $(V,\theta )$
compatible with
$(V,\theta )$
compatible with
![]() $C$
. We have the decomposition
$C$
. We have the decomposition
Let
![]() $\det (C^{[k]})$
denote the induced symmetric pairings of
$\det (C^{[k]})$
denote the induced symmetric pairings of
![]() $(\det (V^{[k]}),{\mathop{\textrm{tr}}\nolimits }(\theta ^{[k]}))$
. Note that
$(\det (V^{[k]}),{\mathop{\textrm{tr}}\nolimits }(\theta ^{[k]}))$
. Note that
![]() $\det ((\mathcal{V}^C)^{[k]})$
is a meromorphic extension of
$\det ((\mathcal{V}^C)^{[k]})$
is a meromorphic extension of
![]() $(\det (V^{[k]}),{\mathop{\textrm{tr}}\nolimits }(\theta ^{[k]}))$
compatible with
$(\det (V^{[k]}),{\mathop{\textrm{tr}}\nolimits }(\theta ^{[k]}))$
compatible with
![]() $\det (C^{[k]})$
. We have the unique filtered extension
$\det (C^{[k]})$
. We have the unique filtered extension
![]() $\mathcal{P}^C_{\ast }\det ((\mathcal{V}^C)^{[k]})$
of
$\mathcal{P}^C_{\ast }\det ((\mathcal{V}^C)^{[k]})$
of
![]() $(\det (V^{[k]}),{\mathop{\textrm{tr}}\nolimits }(\theta ^{[k]}))$
compatible with
$(\det (V^{[k]}),{\mathop{\textrm{tr}}\nolimits }(\theta ^{[k]}))$
compatible with
![]() $\det (C^{[k]})$
. We obtain the decomposable filtered Higgs bundle
$\det (C^{[k]})$
. We obtain the decomposable filtered Higgs bundle
![]() $(\mathcal{P}^{\star }_{\ast }(\mathcal{V}^C),\theta )$
determined by the tuple
$(\mathcal{P}^{\star }_{\ast }(\mathcal{V}^C),\theta )$
determined by the tuple
![]() $\mathcal{P}^C_{\ast }\det ((\mathcal{V}^C)^{[k]})$
as in Proposition 5.13.
$\mathcal{P}^C_{\ast }\det ((\mathcal{V}^C)^{[k]})$
as in Proposition 5.13.
Proposition 5.16. The following holds:
![]() $\mathcal{P}^C_{\ast }(\mathcal{V}^C)=\mathcal{P}^{\star }_{\ast }(\mathcal{V}^C)$
.
$\mathcal{P}^C_{\ast }(\mathcal{V}^C)=\mathcal{P}^{\star }_{\ast }(\mathcal{V}^C)$
.
Proof.
The filtered Higgs bundle
![]() $(\mathcal{P}^C_{\ast }(\mathcal{V}^C),\theta )$
is decomposable. We have
$(\mathcal{P}^C_{\ast }(\mathcal{V}^C),\theta )$
is decomposable. We have
![]() $\det (\mathcal{P}^C_{\ast }(\mathcal{V}^C)^{[k]}) =\mathcal{P}^C_{\ast }\det ((\mathcal{V}^C)^{[k]}) =\det \mathcal{P}^{\star }_{\ast }((\mathcal{V}^C)^{[k]})$
. Hence, we obtain
$\det (\mathcal{P}^C_{\ast }(\mathcal{V}^C)^{[k]}) =\mathcal{P}^C_{\ast }\det ((\mathcal{V}^C)^{[k]}) =\det \mathcal{P}^{\star }_{\ast }((\mathcal{V}^C)^{[k]})$
. Hence, we obtain
![]() $\mathcal{P}^C_{\ast }(\mathcal{V}^C)=\mathcal{P}^{\star }_{\ast }(\mathcal{V}^C)$
by the uniqueness.
$\mathcal{P}^C_{\ast }(\mathcal{V}^C)=\mathcal{P}^{\star }_{\ast }(\mathcal{V}^C)$
by the uniqueness.
Corollary 5.17.
Let
![]() $\mathcal{P}_{\ast }(\mathcal{V}^C)$
be a filtered extension of
$\mathcal{P}_{\ast }(\mathcal{V}^C)$
be a filtered extension of
![]() $(V,\theta )$
satisfying the following conditions:
$(V,\theta )$
satisfying the following conditions:
-
–
 $C$
is perfect with respect to
$C$
is perfect with respect to
 $\mathcal{P}_{\ast }(\mathcal{V}^C)$
;
$\mathcal{P}_{\ast }(\mathcal{V}^C)$
; -
–
 $\mathcal{P}_{\ast }\mathcal{V}^C=\bigoplus _{k\in S} \mathcal{P}_{\ast }((\mathcal{V}^C)^{[k]})$
.
$\mathcal{P}_{\ast }\mathcal{V}^C=\bigoplus _{k\in S} \mathcal{P}_{\ast }((\mathcal{V}^C)^{[k]})$
.
Let
![]() $\mathcal{P}^{\star }_{\ast }(\mathcal{V})$
be the decomposable filtered extension of
$\mathcal{P}^{\star }_{\ast }(\mathcal{V})$
be the decomposable filtered extension of
![]() $(V,\theta )$
determined by the filtered bundles
$(V,\theta )$
determined by the filtered bundles
![]() $\det \bigl (\mathcal{P}_{\ast }((\mathcal{V}^C)^{[k]})\bigr )$
$\det \bigl (\mathcal{P}_{\ast }((\mathcal{V}^C)^{[k]})\bigr )$
![]() $(k\in S)$
. Then,
$(k\in S)$
. Then,
![]() $\mathcal{P}^C_{\ast }(\mathcal{V}^C)=\mathcal{P}^{\star }_{\ast }(\mathcal{V}^C)$
.
$\mathcal{P}^C_{\ast }(\mathcal{V}^C)=\mathcal{P}^{\star }_{\ast }(\mathcal{V}^C)$
.
Proof.
It follows from
![]() $\det \bigl (\mathcal{P}_{\ast }((\mathcal{V}^C)^{[k]})\bigr ) =\mathcal{P}^C_{\ast }\det \bigl ((\mathcal{V}^C)^{[k]}\bigr )$
.
$\det \bigl (\mathcal{P}_{\ast }((\mathcal{V}^C)^{[k]})\bigr ) =\mathcal{P}^C_{\ast }\det \bigl ((\mathcal{V}^C)^{[k]}\bigr )$
.
Let
![]() $C$
and
$C$
and
![]() $C'$
be non-degenerate symmetric pairings of
$C'$
be non-degenerate symmetric pairings of
![]() $(V,\theta )$
. Let
$(V,\theta )$
. Let
![]() $C^{[k]}$
and
$C^{[k]}$
and
![]() $C^{\prime [k]}$
$C^{\prime [k]}$
![]() $(k\in S)$
be the induced non-degenerate symmetric pairings of
$(k\in S)$
be the induced non-degenerate symmetric pairings of
![]() $(V^{[k]},\theta ^{[k]})$
. We have the corresponding symmetric pairings
$(V^{[k]},\theta ^{[k]})$
. We have the corresponding symmetric pairings
![]() $C^{[k]}_1$
and
$C^{[k]}_1$
and
![]() $C^{\prime [k]}_1$
of
$C^{\prime [k]}_1$
of
![]() $V^{[k]}_1$
.
$V^{[k]}_1$
.
Corollary 5.18.
Suppose that
![]() $\det (C^{[k]})=\det (C^{\prime [k]})$
for any
$\det (C^{[k]})=\det (C^{\prime [k]})$
for any
![]() $k\in S$
. Then,
$k\in S$
. Then,
![]() $\mathcal{V}^{C}=\mathcal{V}^{C'}$
holds if and only if
$\mathcal{V}^{C}=\mathcal{V}^{C'}$
holds if and only if
![]() $\mathcal{P}^C_{\ast }\mathcal{V}^C=\mathcal{P}^{C'}_{\ast }\mathcal{V}^{C'}$
holds. It is equivalent to the condition that there exist holomorphic functions
$\mathcal{P}^C_{\ast }\mathcal{V}^C=\mathcal{P}^{C'}_{\ast }\mathcal{V}^{C'}$
holds. It is equivalent to the condition that there exist holomorphic functions
![]() $\gamma _1^{[k]}$
$\gamma _1^{[k]}$
![]() $(k\in S)$
on
$(k\in S)$
on
![]() $U^{(r_k)}$
satisfying
$U^{(r_k)}$
satisfying
![]() $C^{\prime [k]}_1=\exp (\gamma _1^{[k]})C^{[k]}_1$
and
$C^{\prime [k]}_1=\exp (\gamma _1^{[k]})C^{[k]}_1$
and
![]() $\sum _{\sigma \in \mathop{\textrm{Gal}}\nolimits (r_k)}\sigma ^{\ast }\gamma ^{[k]}_1=0$
.
$\sum _{\sigma \in \mathop{\textrm{Gal}}\nolimits (r_k)}\sigma ^{\ast }\gamma ^{[k]}_1=0$
.
Proof. The ‘if’ part of the claim is clear. The “only if” part of the claim follows from Corollary 5.17.
5.4 Prolongation of decoupled harmonic bundles
Let
![]() $(V,\theta )$
be a Higgs bundle on
$(V,\theta )$
be a Higgs bundle on
![]() $U^{\ast }$
, which is regular semisimple and wild. Let
$U^{\ast }$
, which is regular semisimple and wild. Let
![]() $h$
be a decoupled harmonic metric of
$h$
be a decoupled harmonic metric of
![]() $(V,\theta )$
. We obtain the good filtered Higgs bundle
$(V,\theta )$
. We obtain the good filtered Higgs bundle
![]() $(\mathcal{P}^h_{\ast }V,\theta )$
on
$(\mathcal{P}^h_{\ast }V,\theta )$
on
![]() $(U,0)$
.
$(U,0)$
.
Lemma 5.19. The filtered Higgs bundle
![]() $(\mathcal{P}^h_{\ast }V,\theta )$
is decomposable.
$(\mathcal{P}^h_{\ast }V,\theta )$
is decomposable.
Proof.
Because the decomposition (34) is orthogonal with respect to
![]() $\varphi _{\ell }^{-1}(h)$
, the claim is clear.
$\varphi _{\ell }^{-1}(h)$
, the claim is clear.
Remark 5.20. If
![]() $h$
is a decoupled harmonic metric of
$h$
is a decoupled harmonic metric of
![]() $(V,\theta )$
, then we obtain that
$(V,\theta )$
, then we obtain that
![]() $\mathcal{P}^h_{\ast }V$
is a filtered bundle without assuming
$\mathcal{P}^h_{\ast }V$
is a filtered bundle without assuming
![]() $\theta$
is wild.
$\theta$
is wild.
We have the decomposition
![]() $\mathcal{P}^h_{\ast }(V)=\bigoplus _{k\in S}\mathcal{P}^h_{\ast }(V^{[k]})$
. We obtain the filtered extensions
$\mathcal{P}^h_{\ast }(V)=\bigoplus _{k\in S}\mathcal{P}^h_{\ast }(V^{[k]})$
. We obtain the filtered extensions
![]() $\det (\mathcal{P}^h_{\ast }V^{[k]}) =\mathcal{P}^{\det (h)}_{\ast }\det (V^{[k]})$
of
$\det (\mathcal{P}^h_{\ast }V^{[k]}) =\mathcal{P}^{\det (h)}_{\ast }\det (V^{[k]})$
of
![]() $\det (V^{[k]})$
. We have the filtered bundle
$\det (V^{[k]})$
. We have the filtered bundle
![]() $\mathcal{P}^{\star }_{\ast }(\mathcal{V})$
over
$\mathcal{P}^{\star }_{\ast }(\mathcal{V})$
over
![]() $\mathcal{V}=\mathcal{P}^hV$
determined by
$\mathcal{V}=\mathcal{P}^hV$
determined by
![]() $\det (\mathcal{P}^h_{\ast }V^{[k]})$
as in Proposition 5.13.
$\det (\mathcal{P}^h_{\ast }V^{[k]})$
as in Proposition 5.13.
Lemma 5.21.
We have
![]() $\mathcal{P}^h_{\ast }(V) =\mathcal{P}^{\star }_{\ast }(\mathcal{V})$
.
$\mathcal{P}^h_{\ast }(V) =\mathcal{P}^{\star }_{\ast }(\mathcal{V})$
.
Proof.
This follows from the uniqueness of the decomposable filtered extension
![]() $\mathcal{P}^{\star }_{\ast }(\mathcal{V})$
of
$\mathcal{P}^{\star }_{\ast }(\mathcal{V})$
of
![]() $(V,\theta )$
satisfying the condition in Proposition 5.13.
$(V,\theta )$
satisfying the condition in Proposition 5.13.
The decomposition (36) is orthogonal with respect to
![]() $h$
. Let
$h$
. Let
![]() $h^{[k]}$
denote the induced decoupled harmonic metric of
$h^{[k]}$
denote the induced decoupled harmonic metric of
![]() $(V^{[k]},\theta ^{[k]})$
$(V^{[k]},\theta ^{[k]})$
![]() $(k\in S)$
. The decomposition (37) is orthogonal with respect to
$(k\in S)$
. The decomposition (37) is orthogonal with respect to
![]() $\varphi _{r_k}^{\ast }(h^{[k]})$
. Let
$\varphi _{r_k}^{\ast }(h^{[k]})$
. Let
![]() $h^{[k]}_1$
denote the induced flat metric of
$h^{[k]}_1$
denote the induced flat metric of
![]() $V^{[k]}_1$
.
$V^{[k]}_1$
.
Let
![]() $h'$
be another decoupled harmonic metric of
$h'$
be another decoupled harmonic metric of
![]() $(V,\theta )$
. Similarly, we obtain the induced decomposable harmonic metric
$(V,\theta )$
. Similarly, we obtain the induced decomposable harmonic metric
![]() $h^{\prime [k]}$
of
$h^{\prime [k]}$
of
![]() $(V^{[k]},\theta ^{[k]})$
and the induced flat metric
$(V^{[k]},\theta ^{[k]})$
and the induced flat metric
![]() $h^{\prime [k]}_1$
of
$h^{\prime [k]}_1$
of
![]() $V^{[k]}_1$
.
$V^{[k]}_1$
.
Corollary 5.22.
Suppose that
![]() $\det (h^{[k]})=\det (h^{\prime [k]})$
for any
$\det (h^{[k]})=\det (h^{\prime [k]})$
for any
![]() $k\in S$
. Then,
$k\in S$
. Then,
![]() $\mathcal{P}^hV=\mathcal{P}^{h'}V$
hold if and only if
$\mathcal{P}^hV=\mathcal{P}^{h'}V$
hold if and only if
![]() $\mathcal{P}^{h}_{\ast }(V)=\mathcal{P}^{h'}_{\ast }(V)$
holds. This is equivalent to the condition that there uniquely exist holomorphic functions
$\mathcal{P}^{h}_{\ast }(V)=\mathcal{P}^{h'}_{\ast }(V)$
holds. This is equivalent to the condition that there uniquely exist holomorphic functions
![]() $\gamma _1^{[k]}$
$\gamma _1^{[k]}$
![]() $(k\in S)$
on
$(k\in S)$
on
![]() $U^{(r_k)}$
such that (i)
$U^{(r_k)}$
such that (i)
![]() $h^{\prime [k]}_{1}=\exp (2{\mathop{\textrm{Re}}\nolimits }(\gamma _1^{[k]}))h^{[k]}_1$
and (ii)
$h^{\prime [k]}_{1}=\exp (2{\mathop{\textrm{Re}}\nolimits }(\gamma _1^{[k]}))h^{[k]}_1$
and (ii)
![]() $\sum _{\sigma \in \mathop{\textrm{Gal}}\nolimits (r_k)} \sigma ^{\ast }\gamma _1^{[k]}=0$
.
$\sum _{\sigma \in \mathop{\textrm{Gal}}\nolimits (r_k)} \sigma ^{\ast }\gamma _1^{[k]}=0$
.
Proof. The ‘if’ part of the claim is clear. The “only if” part of the claim follows from Lemma 5.21. The second claim is clear.
5.5 Decoupled harmonic metrics and symmetric products
5.5.1 Comparison of extensions
Let
![]() $(V,\theta )$
be a Higgs bundle on
$(V,\theta )$
be a Higgs bundle on
![]() $U^{\ast }$
which is regular semisimple and wild. Let
$U^{\ast }$
which is regular semisimple and wild. Let
![]() $C$
be a non-degenerate symmetric pairing of
$C$
be a non-degenerate symmetric pairing of
![]() $(V,\theta )$
. There exists a unique decoupled harmonic metric
$(V,\theta )$
. There exists a unique decoupled harmonic metric
![]() $h^C$
of
$h^C$
of
![]() $(V,\theta )$
compatible with
$(V,\theta )$
compatible with
![]() $C$
.
$C$
.
Lemma 5.23.
We have
![]() $\mathcal{P}^{h^C}_{\ast }(V)=\mathcal{P}^C_{\ast }(\mathcal{V}^C)$
.
$\mathcal{P}^{h^C}_{\ast }(V)=\mathcal{P}^C_{\ast }(\mathcal{V}^C)$
.
Proof.
By the pull back via
![]() $\varphi _{\ell }$
, it is enough to consider the case
$\varphi _{\ell }$
, it is enough to consider the case
![]() $\mathop{\textrm{rank}}\nolimits V=1$
, which is easy to check.
$\mathop{\textrm{rank}}\nolimits V=1$
, which is easy to check.
5.5.2 Symmetric products compatible with a decoupled harmonic metric
The following lemma is a special case of Lemma 2.7.
Lemma 5.24.
Suppose
![]() $\mathop{\textrm{rank}}\nolimits V=1$
. Let
$\mathop{\textrm{rank}}\nolimits V=1$
. Let
![]() $h$
be a flat metric of
$h$
be a flat metric of
![]() $V$
. There exists a holomorphic non-degenerate symmetric product
$V$
. There exists a holomorphic non-degenerate symmetric product
![]() $C$
of
$C$
of
![]() $V$
which is compatible with
$V$
which is compatible with
![]() $h$
if and only if the monodromy of the Chern connection of
$h$
if and only if the monodromy of the Chern connection of
![]() $h$
is
$h$
is
![]() $1$
or
$1$
or
![]() $-1$
. It is equivalent to the condition
$-1$
. It is equivalent to the condition
If
![]() $C'$
is another non-degenerate symmetric pairing of
$C'$
is another non-degenerate symmetric pairing of
![]() $V$
which is compatible with
$V$
which is compatible with
![]() $h$
, there exists a non-zero constant
$h$
, there exists a non-zero constant
![]() $\alpha$
such that (i)
$\alpha$
such that (i)
![]() $C'=\alpha C$
and (ii)
$C'=\alpha C$
and (ii)
![]() $|\alpha |=1$
.
$|\alpha |=1$
.
Proposition 5.25.
Let
![]() $h$
be a decoupled harmonic metric of
$h$
be a decoupled harmonic metric of
![]() $(V,\theta )$
. Suppose that there exist non-degenerate symmetric products
$(V,\theta )$
. Suppose that there exist non-degenerate symmetric products
![]() $C_{\det (V^{[k]})}$
$C_{\det (V^{[k]})}$
![]() $(k\in S)$
of
$(k\in S)$
of
![]() $\det (V^{[k]})$
which are compatible with
$\det (V^{[k]})$
which are compatible with
![]() $\det (h^{[k]})$
.
$\det (h^{[k]})$
.
-
– There exists a non-degenerate symmetric pairing
 $C$
of
$C$
of
 $(V,\theta )$
such that (i)
$(V,\theta )$
such that (i)
 $C$
is compatible with
$C$
is compatible with
 $h$
and (ii)
$h$
and (ii)
 $\det (C^{[k]})=C_{\det (V^{[k]})}$
.
$\det (C^{[k]})=C_{\det (V^{[k]})}$
. -
– If
 $C'$
is another non-degenerate symmetric pairing of
$C'$
is another non-degenerate symmetric pairing of
 $(V,\theta )$
satisfying the above conditions (i) and (ii), then there exist
$(V,\theta )$
satisfying the above conditions (i) and (ii), then there exist
 $r_k$
-roots
$r_k$
-roots
 $\mu _k$
of
$\mu _k$
of
 $1$
such that
$1$
such that
 $C^{\prime [k]}=\mu _k C^{[k]}$
.
$C^{\prime [k]}=\mu _k C^{[k]}$
.
Proof.
Let
![]() $h^{[k]}_1$
$h^{[k]}_1$
![]() $(k\in S)$
be the induced flat metrics of
$(k\in S)$
be the induced flat metrics of
![]() $V^{[k]}_1$
. By Lemma 2.7, Proposition 5.13 and Lemma 5.24, there exist non-degenerate symmetric products
$V^{[k]}_1$
. By Lemma 2.7, Proposition 5.13 and Lemma 5.24, there exist non-degenerate symmetric products
![]() $C^{[k]}_1$
of
$C^{[k]}_1$
of
![]() $V^{[k]}_1$
compatible with
$V^{[k]}_1$
compatible with
![]() $h^{[k]}_1$
for any
$h^{[k]}_1$
for any
![]() $k\in S$
. They induce non-degenerate symmetric products
$k\in S$
. They induce non-degenerate symmetric products
![]() $C^{[k]}$
of
$C^{[k]}$
of
![]() $(V^{[k]},\theta ^{[k]})$
. Because
$(V^{[k]},\theta ^{[k]})$
. Because
![]() $\det (C^{[k]})$
is compatible with
$\det (C^{[k]})$
is compatible with
![]() $\det h^{[k]}$
, there exist constants
$\det h^{[k]}$
, there exist constants
![]() $\alpha _k$
such that
$\alpha _k$
such that
![]() $\det (C^{[k]})=\alpha _k\cdot C_{\det (V^{[k]})}$
and
$\det (C^{[k]})=\alpha _k\cdot C_{\det (V^{[k]})}$
and
![]() $|\alpha _k|=1$
. By replacing
$|\alpha _k|=1$
. By replacing
![]() $C^{[k]}$
with
$C^{[k]}$
with
![]() $\alpha _k^{1/r_k}C^{[k]}$
, we obtain the first claim. The second claim is also clear.
$\alpha _k^{1/r_k}C^{[k]}$
, we obtain the first claim. The second claim is also clear.
5.5.3 Existence
Let
![]() $\mathcal{V}$
be a meromorphic extension of
$\mathcal{V}$
be a meromorphic extension of
![]() $(V,\theta )$
.
$(V,\theta )$
.
Lemma 5.26.
Let
![]() $C_{\det (V^{[k]})}$
be non-degenerate symmetric pairings of
$C_{\det (V^{[k]})}$
be non-degenerate symmetric pairings of
![]() $\det (V^{[k]})$
such that
$\det (V^{[k]})$
such that
![]() $\det (\mathcal{V}^{[k]})$
is compatible with
$\det (\mathcal{V}^{[k]})$
is compatible with
![]() $C_{\det (V^{[k]})}$
. Then, there exists a non-degenerate symmetric pairing
$C_{\det (V^{[k]})}$
. Then, there exists a non-degenerate symmetric pairing
![]() $C$
of
$C$
of
![]() $(V,\theta )$
such that (i)
$(V,\theta )$
such that (i)
![]() $\det (C^{[k]})=C_{\det (\mathcal{V}^{[k]})}$
and (ii)
$\det (C^{[k]})=C_{\det (\mathcal{V}^{[k]})}$
and (ii)
![]() $\mathcal{V}^C=\mathcal{V}$
.
$\mathcal{V}^C=\mathcal{V}$
.
Proof.
It is enough to consider the case
![]() $|S|=1$
. We omit the superscript
$|S|=1$
. We omit the superscript
![]() $[k]$
and the subscript
$[k]$
and the subscript
![]() $k$
. We use the notation in the proof of Proposition 5.13. Let
$k$
. We use the notation in the proof of Proposition 5.13. Let
![]() $C'_{1,\beta (1)}$
be a non-degenerate symmetric pairing of
$C'_{1,\beta (1)}$
be a non-degenerate symmetric pairing of
![]() $\mathcal{V}_{\beta (1)}$
. We obtain a
$\mathcal{V}_{\beta (1)}$
. We obtain a
![]() $\mathop{\textrm{Gal}}\nolimits (r)$
-invariant non-degenerate symmetric pairing
$\mathop{\textrm{Gal}}\nolimits (r)$
-invariant non-degenerate symmetric pairing
![]() $\bigoplus _{\sigma \in \mathop{\textrm{Gal}}\nolimits (r)}\sigma ^{\ast }C'_{1,\beta (1)}$
of
$\bigoplus _{\sigma \in \mathop{\textrm{Gal}}\nolimits (r)}\sigma ^{\ast }C'_{1,\beta (1)}$
of
![]() $\mathcal{V}^{(r)}$
. It induces a non-degenerate symmetric pairing
$\mathcal{V}^{(r)}$
. It induces a non-degenerate symmetric pairing
![]() $C'$
of
$C'$
of
![]() $\mathcal{V}$
. From
$\mathcal{V}$
. From
![]() $C''_{1,\beta (1)}=\zeta C'_{1,\beta (1)}$
, we obtain another non-degenerate symmetric pairing
$C''_{1,\beta (1)}=\zeta C'_{1,\beta (1)}$
, we obtain another non-degenerate symmetric pairing
![]() $C''$
, for which we have
$C''$
, for which we have
![]() $\det (C'')=z\det (C')$
.
$\det (C'')=z\det (C')$
.
Let
![]() $\alpha$
be the holomorphic function on
$\alpha$
be the holomorphic function on
![]() $U^{\ast }$
determined by
$U^{\ast }$
determined by
![]() $\det (C')=\alpha \cdot C_{\det (V)}$
. By the above consideration, we may assume that
$\det (C')=\alpha \cdot C_{\det (V)}$
. By the above consideration, we may assume that
![]() $\alpha$
induces a nowhere vanishing holomorphic function on
$\alpha$
induces a nowhere vanishing holomorphic function on
![]() $U$
. By choosing an
$U$
. By choosing an
![]() $r$
th root
$r$
th root
![]() $\alpha ^{1/r}$
of
$\alpha ^{1/r}$
of
![]() $\alpha$
, and by setting
$\alpha$
, and by setting
![]() $C=\alpha ^{-1/r}C'$
, we obtain a desired non-degenerate pairing
$C=\alpha ^{-1/r}C'$
, we obtain a desired non-degenerate pairing
![]() $C$
.
$C$
.
We can prove the following lemma similarly.
Lemma 5.27.
Let
![]() $h_{\det (V^{[k]})}$
be flat metrics of
$h_{\det (V^{[k]})}$
be flat metrics of
![]() $\det (V^{[k]})$
such that
$\det (V^{[k]})$
such that
![]() $\det (\mathcal{V}^{[k]})=\mathcal{P}^{h_{\det (V^{[k]})}}(\det (V^{[k]}))$
. There exists a decoupled harmonic metric
$\det (\mathcal{V}^{[k]})=\mathcal{P}^{h_{\det (V^{[k]})}}(\det (V^{[k]}))$
. There exists a decoupled harmonic metric
![]() $h$
of
$h$
of
![]() $(V,\theta )$
such that (i)
$(V,\theta )$
such that (i)
![]() $\det (h^{[k]})=h_{\det (V^{[k]})}$
and (ii)
$\det (h^{[k]})=h_{\det (V^{[k]})}$
and (ii)
![]() $\mathcal{P}^h(V)=\mathcal{V}$
.
$\mathcal{P}^h(V)=\mathcal{V}$
.
5.6 Global case
5.6.1 Meromorphic extensions and filtered extensions
Let
![]() $Y$
be a Riemann surface with a discrete subset
$Y$
be a Riemann surface with a discrete subset
![]() $D$
. Let
$D$
. Let
![]() $\iota _{Y\setminus D}\colon Y\setminus D\to Y$
denote the inclusion. For a holomorphic vector bundle
$\iota _{Y\setminus D}\colon Y\setminus D\to Y$
denote the inclusion. For a holomorphic vector bundle
![]() $V$
on
$V$
on
![]() $Y\setminus D$
, a meromorphic extension of
$Y\setminus D$
, a meromorphic extension of
![]() $V$
to
$V$
to
![]() $(Y,D)$
is defined to be a locally free
$(Y,D)$
is defined to be a locally free
![]() $\mathcal{O}_Y(\ast D)$
-submodule
$\mathcal{O}_Y(\ast D)$
-submodule
![]() $\mathcal{V}$
of
$\mathcal{V}$
of
![]() $(\iota _{Y\setminus D})_{\ast }V$
such that
$(\iota _{Y\setminus D})_{\ast }V$
such that
![]() $\mathcal{V}_{|Y\setminus D}=V$
. A filtered extension of
$\mathcal{V}_{|Y\setminus D}=V$
. A filtered extension of
![]() $V$
to
$V$
to
![]() $(Y,D)$
is a filtered bundle
$(Y,D)$
is a filtered bundle
![]() $\mathcal{P}_{\ast }\mathcal{V}$
over a meromorphic extension
$\mathcal{P}_{\ast }\mathcal{V}$
over a meromorphic extension
![]() $\mathcal{V}$
of
$\mathcal{V}$
of
![]() $V$
. We use similar terminology for non-degenerate symmetric parings and Higgs bundles in this situation.
$V$
. We use similar terminology for non-degenerate symmetric parings and Higgs bundles in this situation.
5.6.2 Decomposable filtered extensions
Let
![]() $(V,\theta )$
be a regular semisimple Higgs bundle on
$(V,\theta )$
be a regular semisimple Higgs bundle on
![]() $Y\setminus D$
which is wild along
$Y\setminus D$
which is wild along
![]() $D$
. Let
$D$
. Let
![]() $\mathcal{P}_{\ast }\mathcal{V}$
be a filtered extension of
$\mathcal{P}_{\ast }\mathcal{V}$
be a filtered extension of
![]() $(V,\theta )$
to
$(V,\theta )$
to
![]() $(Y,D)$
.
$(Y,D)$
.
Definition 5.28.
![]() $\mathcal{P}_{\ast }\mathcal{V}$
is called a decomposable filtered extension of
$\mathcal{P}_{\ast }\mathcal{V}$
is called a decomposable filtered extension of
![]() $(V,\theta )$
if the restriction to a neighbourhood of any
$(V,\theta )$
if the restriction to a neighbourhood of any
![]() $P\in D$
is decomposable.
$P\in D$
is decomposable.
The following lemma is clear.
Lemma 5.29.
A decomposable filtered Higgs bundle
![]() $(\mathcal{P}_{\ast }\mathcal{V},\theta )$
is a good filtered Higgs bundle. Any decomposition
$(\mathcal{P}_{\ast }\mathcal{V},\theta )$
is a good filtered Higgs bundle. Any decomposition
![]() $(\mathcal{V},\theta )_{|Y\setminus D}= (V_1,\theta _1)\oplus (V_2,\theta _2)$
extends to a decomposition
$(\mathcal{V},\theta )_{|Y\setminus D}= (V_1,\theta _1)\oplus (V_2,\theta _2)$
extends to a decomposition
![]() $(\mathcal{P}_{\ast}\mathcal{V},\theta )= (\mathcal{P}_{\ast }\mathcal{V}_1,\theta _1) \oplus (\mathcal{P}_{\ast }\mathcal{V}_2,\theta _2)$
.
$(\mathcal{P}_{\ast}\mathcal{V},\theta )= (\mathcal{P}_{\ast }\mathcal{V}_1,\theta _1) \oplus (\mathcal{P}_{\ast }\mathcal{V}_2,\theta _2)$
.
We have the line bundle
![]() $L_V$
on
$L_V$
on
![]() $\Sigma _{V,\theta }$
corresponding to
$\Sigma _{V,\theta }$
corresponding to
![]() $(V,\theta )$
. Let
$(V,\theta )$
. Let
![]() $\mathbb{P}(T^{\ast }Y)$
be the projective completion of
$\mathbb{P}(T^{\ast }Y)$
be the projective completion of
![]() $T^{\ast }Y$
. Let
$T^{\ast }Y$
. Let
![]() $Z$
be the closure of
$Z$
be the closure of
![]() $\Sigma _{V,\theta }\subset T^{\ast }(Y\setminus D)$
in
$\Sigma _{V,\theta }\subset T^{\ast }(Y\setminus D)$
in
![]() $\mathbb{P}(T^{\ast }Y)$
. Let
$\mathbb{P}(T^{\ast }Y)$
. Let
![]() $\widetilde{\Sigma }_{V,\theta }\to Z$
denote the normalization. We may naturally regard
$\widetilde{\Sigma }_{V,\theta }\to Z$
denote the normalization. We may naturally regard
![]() $\widetilde{\Sigma }_{V,\theta }$
as a partial compactification of
$\widetilde{\Sigma }_{V,\theta }$
as a partial compactification of
![]() $\Sigma _{V,\theta }$
. We set
$\Sigma _{V,\theta }$
. We set
![]() $\widetilde{D}=\widetilde{\Sigma }_{V,\theta }\setminus \Sigma _{V,\theta }$
. The morphism
$\widetilde{D}=\widetilde{\Sigma }_{V,\theta }\setminus \Sigma _{V,\theta }$
. The morphism
![]() $\pi :\Sigma _{V,\theta }\to Y\setminus D$
uniquely extends to a morphism
$\pi :\Sigma _{V,\theta }\to Y\setminus D$
uniquely extends to a morphism
![]() $\widetilde{\pi }:(\widetilde{\Sigma }_{V,\theta },\widetilde{D})\to (Y,D)$
. From a meromorphic extension
$\widetilde{\pi }:(\widetilde{\Sigma }_{V,\theta },\widetilde{D})\to (Y,D)$
. From a meromorphic extension
![]() $\mathcal{L}_V$
of
$\mathcal{L}_V$
of
![]() $L_V$
to
$L_V$
to
![]() $(\widetilde{\Sigma }_{V,\theta },\widetilde{D})$
, we obtain a meromorphic extension
$(\widetilde{\Sigma }_{V,\theta },\widetilde{D})$
, we obtain a meromorphic extension
![]() $\widetilde{\pi }_{\ast }(\mathcal{L}_V)$
of
$\widetilde{\pi }_{\ast }(\mathcal{L}_V)$
of
![]() $(V,\theta )$
to
$(V,\theta )$
to
![]() $(Y,D)$
. From a filtered extension
$(Y,D)$
. From a filtered extension
![]() $\mathcal{P}_{\ast }\mathcal{L}_V$
of
$\mathcal{P}_{\ast }\mathcal{L}_V$
of
![]() $L_V$
to
$L_V$
to
![]() $(\widetilde{\Sigma }_{V,\theta },\widetilde{D})$
, we obtain a decomposable filtered extension
$(\widetilde{\Sigma }_{V,\theta },\widetilde{D})$
, we obtain a decomposable filtered extension
![]() $\widetilde{\pi }_{\ast }(\mathcal{P}_{\ast }\mathcal{L}_V)$
of
$\widetilde{\pi }_{\ast }(\mathcal{P}_{\ast }\mathcal{L}_V)$
of
![]() $(V,\theta )$
to
$(V,\theta )$
to
![]() $(Y,D)$
. The following proposition is a reformulation of Proposition 5.12.
$(Y,D)$
. The following proposition is a reformulation of Proposition 5.12.
Proposition 5.30.
The above procedure induces an equivalence between filtered extensions (respectively meromorphic extensions) of
![]() $L_V$
to
$L_V$
to
![]() $(\widetilde{\Sigma }_{V,\theta },\widetilde{D})$
and decomposable filtered extensions (respectively meromorphic extensions) of
$(\widetilde{\Sigma }_{V,\theta },\widetilde{D})$
and decomposable filtered extensions (respectively meromorphic extensions) of
![]() $(V,\theta )$
to
$(V,\theta )$
to
![]() $(Y,D)$
.
$(Y,D)$
.
5.6.3 Symmetric products
Let
![]() $C$
be a non-degenerate symmetric pairing of
$C$
be a non-degenerate symmetric pairing of
![]() $(V,\theta )$
. We restate Proposition 5.15 in the global setting.
$(V,\theta )$
. We restate Proposition 5.15 in the global setting.
Proposition 5.31.
For a non-degenerate symmetric pairing
![]() $C$
of
$C$
of
![]() $(V,\theta )$
, there uniquely exists a meromorphic extension
$(V,\theta )$
, there uniquely exists a meromorphic extension
![]() $\mathcal{V}^C$
of
$\mathcal{V}^C$
of
![]() $(V,\theta )$
to
$(V,\theta )$
to
![]() $(Y,D)$
compatible with
$(Y,D)$
compatible with
![]() $C$
. Moreover, there uniquely exists a filtered bundle
$C$
. Moreover, there uniquely exists a filtered bundle
![]() $\mathcal{P}^C_{\ast }(\mathcal{V}^C)$
over
$\mathcal{P}^C_{\ast }(\mathcal{V}^C)$
over
![]() $\mathcal{V}^C$
satisfying the following conditions;
$\mathcal{V}^C$
satisfying the following conditions;
-
–
 $C$
is perfect with respect to
$C$
is perfect with respect to
 $\mathcal{P}^C_{\ast }(\mathcal{V}^C)$
;
$\mathcal{P}^C_{\ast }(\mathcal{V}^C)$
; -
–
 $\mathcal{P}^C_{\ast }(\mathcal{V}^C)$
is a decomposable filtered extension of
$\mathcal{P}^C_{\ast }(\mathcal{V}^C)$
is a decomposable filtered extension of
 $(V,\theta )$
.
$(V,\theta )$
.
The decomposable filtered extension
![]() $\mathcal{P}^C_{\ast }(\mathcal{V}^C)$
is described as follows. Let
$\mathcal{P}^C_{\ast }(\mathcal{V}^C)$
is described as follows. Let
![]() $C_0$
be the non-degenerate symmetric pairing of
$C_0$
be the non-degenerate symmetric pairing of
![]() $L_V$
corresponding to
$L_V$
corresponding to
![]() $C$
. There exists the unique filtered extension
$C$
. There exists the unique filtered extension
![]() $\mathcal{P}^{C_0}_{\ast }(\mathcal{L}^{C_0}_V)$
of
$\mathcal{P}^{C_0}_{\ast }(\mathcal{L}^{C_0}_V)$
of
![]() $L_V$
to
$L_V$
to
![]() $(\widetilde{\Sigma }_{V,\theta },\widetilde{D})$
. Then,
$(\widetilde{\Sigma }_{V,\theta },\widetilde{D})$
. Then,
![]() $\mathcal{P}^C_{\ast }(\mathcal{V}^C)= \widetilde{\pi }_{\ast }(\mathcal{P}^{C_0}_{\ast }(\mathcal{L}^{C_0}_V))$
.
$\mathcal{P}^C_{\ast }(\mathcal{V}^C)= \widetilde{\pi }_{\ast }(\mathcal{P}^{C_0}_{\ast }(\mathcal{L}^{C_0}_V))$
.
5.6.4 Decoupled harmonic bundles
Let
![]() $h$
be a decoupled harmonic metric of
$h$
be a decoupled harmonic metric of
![]() $(V,\theta )$
. We obtain the good filtered Higgs bundle
$(V,\theta )$
. We obtain the good filtered Higgs bundle
![]() $(\mathcal{P}^h_{\ast }V,\theta )$
on
$(\mathcal{P}^h_{\ast }V,\theta )$
on
![]() $(Y,D)$
. We obtain the following lemma from Lemma 5.19.
$(Y,D)$
. We obtain the following lemma from Lemma 5.19.
Lemma 5.32. The filtered Higgs bundle
![]() $(\mathcal{P}^h_{\ast }V,\theta )$
is decomposable.
$(\mathcal{P}^h_{\ast }V,\theta )$
is decomposable.
We obtain the following lemma from Lemma 5.23.
Lemma 5.33.
For a non-degenerate symmetric pairing
![]() $C$
of
$C$
of
![]() $(V,\theta )$
, we have
$(V,\theta )$
, we have
![]() $\mathcal{P}^{h^C}_{\ast }(V)=\mathcal{P}^C_{\ast }(\mathcal{V}^C)$
.
$\mathcal{P}^{h^C}_{\ast }(V)=\mathcal{P}^C_{\ast }(\mathcal{V}^C)$
.
5.7 Kobayashi–Hitchin correspondence for decoupled harmonic bundles
Let
![]() $X$
be a compact Riemann surface. Let
$X$
be a compact Riemann surface. Let
![]() $D\subset X$
be a finite subset. Let
$D\subset X$
be a finite subset. Let
![]() $(V,\theta )$
be a regular semisimple Higgs bundle on
$(V,\theta )$
be a regular semisimple Higgs bundle on
![]() $X\setminus D$
, which is wild along
$X\setminus D$
, which is wild along
![]() $D$
. For any decoupled harmonic metric
$D$
. For any decoupled harmonic metric
![]() $h$
of
$h$
of
![]() $(V,\theta )$
we obtain a good filtered Higgs bundle
$(V,\theta )$
we obtain a good filtered Higgs bundle
![]() $(\mathcal{P}^h_{\ast }\mathcal{V},\theta )$
on
$(\mathcal{P}^h_{\ast }\mathcal{V},\theta )$
on
![]() $(X,D)$
which is polystable of degree
$(X,D)$
which is polystable of degree
![]() $0$
. According to Lemma 5.32, it is decomposable.
$0$
. According to Lemma 5.32, it is decomposable.
Conversely, let
![]() $(\mathcal{P}_{\ast }\mathcal{V},\theta )$
be a polystable decomposable filtered Higgs bundle of degree
$(\mathcal{P}_{\ast }\mathcal{V},\theta )$
be a polystable decomposable filtered Higgs bundle of degree
![]() $0$
on
$0$
on
![]() $(X,D)$
such that
$(X,D)$
such that
![]() $(V,\theta )=(\mathcal{V},\theta )_{|X\setminus D}$
is regular semisimple. There exists a harmonic metric
$(V,\theta )=(\mathcal{V},\theta )_{|X\setminus D}$
is regular semisimple. There exists a harmonic metric
![]() $h$
of
$h$
of
![]() $(V,\theta )$
adapted to
$(V,\theta )$
adapted to
![]() $\mathcal{P}_{\ast }\mathcal{V}$
by [Reference Biquard and BoalchBB04, Reference MochizukiMoc21, Reference SimpsonSim90].
$\mathcal{P}_{\ast }\mathcal{V}$
by [Reference Biquard and BoalchBB04, Reference MochizukiMoc21, Reference SimpsonSim90].
Proposition 5.34. The harmonic metric
![]() $h$
is a decoupled harmonic metric.
$h$
is a decoupled harmonic metric.
Proof.
It is enough to consider the case where
![]() $(\mathcal{P}_{\ast }\mathcal{V},\theta )$
is stable. By Lemma 5.29,
$(\mathcal{P}_{\ast }\mathcal{V},\theta )$
is stable. By Lemma 5.29,
![]() $\Sigma _{V,\theta }$
is connected. Let
$\Sigma _{V,\theta }$
is connected. Let
![]() $\mathbb{P}(T^{\ast }X)$
denote the projective completion of
$\mathbb{P}(T^{\ast }X)$
denote the projective completion of
![]() $T^{\ast }X$
. Let
$T^{\ast }X$
. Let
![]() $Z$
denote the closure of
$Z$
denote the closure of
![]() $\Sigma _{V,\theta }$
in
$\Sigma _{V,\theta }$
in
![]() $\mathbb{P}(T^{\ast }X)$
. Let
$\mathbb{P}(T^{\ast }X)$
. Let
![]() $\widetilde{\Sigma }_{V,\theta }\to Z$
denote the normalization. Let
$\widetilde{\Sigma }_{V,\theta }\to Z$
denote the normalization. Let
![]() $\rho :\widetilde{\Sigma }_{V,\theta }\to X$
denote the induced morphism. We set
$\rho :\widetilde{\Sigma }_{V,\theta }\to X$
denote the induced morphism. We set
![]() $\widetilde{D}=\rho ^{-1}(D)$
. Let
$\widetilde{D}=\rho ^{-1}(D)$
. Let
![]() $L_V$
be the line bundle on
$L_V$
be the line bundle on
![]() $\Sigma _{V,\theta }$
corresponding to
$\Sigma _{V,\theta }$
corresponding to
![]() $(V,\theta )$
. Because
$(V,\theta )$
. Because
![]() $\mathcal{P}_{\ast }\mathcal{V}$
is a decomposable filtered extension of
$\mathcal{P}_{\ast }\mathcal{V}$
is a decomposable filtered extension of
![]() $(V,\theta )$
, there exists the corresponding filtered extension
$(V,\theta )$
, there exists the corresponding filtered extension
![]() $\mathcal{P}_{\ast }\mathcal{L}_V$
of
$\mathcal{P}_{\ast }\mathcal{L}_V$
of
![]() $L_V$
on
$L_V$
on
![]() $(\widetilde{\Sigma }_{V,\theta },\widetilde{D})$
. We have
$(\widetilde{\Sigma }_{V,\theta },\widetilde{D})$
. We have
![]() $\rho _{\ast }(\mathcal{P}_{\ast }\mathcal{L})=\mathcal{P}_{\ast }\mathcal{V}$
. By Proposition 5.35 below, we have
$\rho _{\ast }(\mathcal{P}_{\ast }\mathcal{L})=\mathcal{P}_{\ast }\mathcal{V}$
. By Proposition 5.35 below, we have
![]() $\deg (\mathcal{P}_{\ast }\mathcal{L}_V) =\deg (\mathcal{P}_{\ast }\mathcal{V})=0$
. There exists a flat metric
$\deg (\mathcal{P}_{\ast }\mathcal{L}_V) =\deg (\mathcal{P}_{\ast }\mathcal{V})=0$
. There exists a flat metric
![]() $h_{L_V}$
of
$h_{L_V}$
of
![]() $L_V$
adapted to
$L_V$
adapted to
![]() $\mathcal{P}_{\ast }\mathcal{L}_V$
. We obtain a decoupled harmonic metric
$\mathcal{P}_{\ast }\mathcal{L}_V$
. We obtain a decoupled harmonic metric
![]() $h_1$
of
$h_1$
of
![]() $(V,\theta )$
corresponding to
$(V,\theta )$
corresponding to
![]() $h_{L_V}$
, which is adapted to
$h_{L_V}$
, which is adapted to
![]() $\mathcal{P}_{\ast }\mathcal{V}$
. By the stability, there exists a positive constant
$\mathcal{P}_{\ast }\mathcal{V}$
. By the stability, there exists a positive constant
![]() $h=ah_1$
, and hence
$h=ah_1$
, and hence
![]() $h$
is also a decoupled harmonic metric.
$h$
is also a decoupled harmonic metric.
5.7.1 Degree
Let
![]() $\rho :X_1\to X_2$
be a non-constant morphism of compact Riemann surfaces. Let
$\rho :X_1\to X_2$
be a non-constant morphism of compact Riemann surfaces. Let
![]() $D_2\subset X_2$
be a finite subset. We set
$D_2\subset X_2$
be a finite subset. We set
![]() $D_1=\rho ^{-1}(D_2)$
. Let
$D_1=\rho ^{-1}(D_2)$
. Let
![]() $\mathcal{P}_{\ast }\mathcal{V}$
be a filtered bundle on
$\mathcal{P}_{\ast }\mathcal{V}$
be a filtered bundle on
![]() $(X_1,D_1)$
. We obtain a filtered bundle
$(X_1,D_1)$
. We obtain a filtered bundle
![]() $\rho _{\ast }(\mathcal{P}_{\ast }\mathcal{V})$
on
$\rho _{\ast }(\mathcal{P}_{\ast }\mathcal{V})$
on
![]() $(X_2,D_2)$
. Let
$(X_2,D_2)$
. Let
![]() $m(P)$
denote the ramification index of
$m(P)$
denote the ramification index of
![]() $\rho$
at
$\rho$
at
![]() $P\in X_1$
.
$P\in X_1$
.
Proposition 5.35. The following holds:
 \begin{align*} \deg (\rho _{\ast }(\mathcal {P}_{\ast }\mathcal {V})) =\deg (\mathcal {P}_{\ast }\mathcal {V}) -\frac {\mathop {\textrm {rank}}\nolimits \mathcal {V}}{2} \sum _{P\in X_1\setminus D_1} (m(P)-1). \end{align*}
\begin{align*} \deg (\rho _{\ast }(\mathcal {P}_{\ast }\mathcal {V})) =\deg (\mathcal {P}_{\ast }\mathcal {V}) -\frac {\mathop {\textrm {rank}}\nolimits \mathcal {V}}{2} \sum _{P\in X_1\setminus D_1} (m(P)-1). \end{align*}
Proof.
We have
![]() $\mathcal{P}_0(\rho _{\ast }\mathcal{V})=\rho _{\ast }(\mathcal{P}_0\mathcal{V})$
. By the Grothendieck–Riemann–Roch theorem and the Riemann–Hurwitz formula, we have
$\mathcal{P}_0(\rho _{\ast }\mathcal{V})=\rho _{\ast }(\mathcal{P}_0\mathcal{V})$
. By the Grothendieck–Riemann–Roch theorem and the Riemann–Hurwitz formula, we have
 \begin{align*} \deg (\rho _{\ast }\mathcal {P}_0\mathcal {V}) =\deg (\mathcal {P}_0\mathcal {V}) -\frac {\mathop {\textrm {rank}}\nolimits \mathcal {V}}{2}\sum _{P\in X_1}(m(P)-1). \end{align*}
\begin{align*} \deg (\rho _{\ast }\mathcal {P}_0\mathcal {V}) =\deg (\mathcal {P}_0\mathcal {V}) -\frac {\mathop {\textrm {rank}}\nolimits \mathcal {V}}{2}\sum _{P\in X_1}(m(P)-1). \end{align*}
By the construction of
![]() $\rho _{\ast }(\mathcal{P}_{\ast }\mathcal{V})$
, we obtain
$\rho _{\ast }(\mathcal{P}_{\ast }\mathcal{V})$
, we obtain
 \begin{align} &\deg (\rho _{\ast }(\mathcal{P}_{\ast }\mathcal{V})) =\deg (\rho _{\ast }(\mathcal{P}_0\mathcal{V})) -\sum _{a\in D_1} \sum _{-1\lt a\leqslant 0} \sum _{j=0}^{m(P)-1} \left ( {a-j \over m(P)} \right ) \dim \mathop{\textrm{Gr}}\nolimits ^{\mathcal{P}}_a(\mathcal{V}_P)\nonumber \\[5pt] &\qquad =\deg (\mathcal{P}_0\mathcal{V}) -{\mathop{\textrm{rank}}\nolimits \mathcal{V} \over 2}\sum _{P\in X_1}(m(P)-1) -\sum _{P\in D_1}\sum _{-1\lt a\leqslant 0} \left ( a-{1 \over 2}(m(P)-1) \right ) \dim \mathop{\textrm{Gr}}\nolimits ^{\mathcal{P}}_a(\mathcal{V}_P)\nonumber \\[5pt] &\qquad \qquad \qquad =\deg (\mathcal{P}_{\ast }\mathcal{V}) -{\mathop{\textrm{rank}}\nolimits \mathcal{V} \over 2}\sum _{P\in X_1\setminus D_1} (m(P)-1). \end{align}
\begin{align} &\deg (\rho _{\ast }(\mathcal{P}_{\ast }\mathcal{V})) =\deg (\rho _{\ast }(\mathcal{P}_0\mathcal{V})) -\sum _{a\in D_1} \sum _{-1\lt a\leqslant 0} \sum _{j=0}^{m(P)-1} \left ( {a-j \over m(P)} \right ) \dim \mathop{\textrm{Gr}}\nolimits ^{\mathcal{P}}_a(\mathcal{V}_P)\nonumber \\[5pt] &\qquad =\deg (\mathcal{P}_0\mathcal{V}) -{\mathop{\textrm{rank}}\nolimits \mathcal{V} \over 2}\sum _{P\in X_1}(m(P)-1) -\sum _{P\in D_1}\sum _{-1\lt a\leqslant 0} \left ( a-{1 \over 2}(m(P)-1) \right ) \dim \mathop{\textrm{Gr}}\nolimits ^{\mathcal{P}}_a(\mathcal{V}_P)\nonumber \\[5pt] &\qquad \qquad \qquad =\deg (\mathcal{P}_{\ast }\mathcal{V}) -{\mathop{\textrm{rank}}\nolimits \mathcal{V} \over 2}\sum _{P\in X_1\setminus D_1} (m(P)-1). \end{align}
Thus, we are done.
Remark 5.36. If there is no ramification point in
![]() $X_1\setminus D_1$
, we have
$X_1\setminus D_1$
, we have
![]() $\deg (\mathcal{P}_{\ast }\mathcal{V})=\deg (\rho _{\ast }\mathcal{P}_{\ast }\mathcal{V})$
. We can also prove it as follows. Let
$\deg (\mathcal{P}_{\ast }\mathcal{V})=\deg (\rho _{\ast }\mathcal{P}_{\ast }\mathcal{V})$
. We can also prove it as follows. Let
![]() $h_0$
be a Hermitian metric of
$h_0$
be a Hermitian metric of
![]() $\mathcal{V}_{|X_1\setminus D_1}$
such that (i)
$\mathcal{V}_{|X_1\setminus D_1}$
such that (i)
![]() $h_0$
is flat around any point of
$h_0$
is flat around any point of
![]() $D_1$
and (ii)
$D_1$
and (ii)
![]() $h_0$
is adapted to
$h_0$
is adapted to
![]() $\mathcal{P}_{\ast }\mathcal{V}$
. Let
$\mathcal{P}_{\ast }\mathcal{V}$
. Let
![]() $R(h_0)$
be the curvature of the Chern connection of
$R(h_0)$
be the curvature of the Chern connection of
![]() $h$
. Then, we have
$h$
. Then, we have
We have the induced metric
![]() $\rho _{\ast }(h_0)$
of
$\rho _{\ast }(h_0)$
of
![]() $\rho _{\ast }(\mathcal{V})_{|X_2\setminus D_2}$
. It is flat around any point of
$\rho _{\ast }(\mathcal{V})_{|X_2\setminus D_2}$
. It is flat around any point of
![]() $D_2$
, and it is adapted to
$D_2$
, and it is adapted to
![]() $\rho _{\ast }(\mathcal{P}_{\ast }\mathcal{V})$
. Hence, we have
$\rho _{\ast }(\mathcal{P}_{\ast }\mathcal{V})$
. Hence, we have
Then, we obtain
![]() $\deg (\mathcal{P}_{\ast }\mathcal{V})=\deg (\rho _{\ast }\mathcal{P}_{\ast }\mathcal{V})$
.
$\deg (\mathcal{P}_{\ast }\mathcal{V})=\deg (\rho _{\ast }\mathcal{P}_{\ast }\mathcal{V})$
.
5.8 Dirichlet problem for wild decoupled harmonic bundles
Let
![]() $Y$
,
$Y$
,
![]() $X$
,
$X$
,
![]() $D$
and
$D$
and
![]() $(\mathcal{P}_{\ast }\mathcal{V},\theta )$
be as in §2.3.
$(\mathcal{P}_{\ast }\mathcal{V},\theta )$
be as in §2.3.
Proposition 5.37.
Assume that
![]() $(V,\theta )$
is regular semisimple and that
$(V,\theta )$
is regular semisimple and that
![]() $\mathcal{P}_{\ast }(\mathcal{V})$
is a decomposable filtered extension. Then, the harmonic metric
$\mathcal{P}_{\ast }(\mathcal{V})$
is a decomposable filtered extension. Then, the harmonic metric
![]() $h$
in Theorem
2.8
is decoupled.
$h$
in Theorem
2.8
is decoupled.
Proof.
It is enough to consider the case where
![]() $\Sigma _{V,\theta }$
is connected. Let
$\Sigma _{V,\theta }$
is connected. Let
![]() $\widetilde{\Sigma }_{V,\theta }$
be the partial compactification of
$\widetilde{\Sigma }_{V,\theta }$
be the partial compactification of
![]() $\Sigma _{V,\theta }$
as in §5.6.2. Let
$\Sigma _{V,\theta }$
as in §5.6.2. Let
![]() $\widetilde{X}$
and
$\widetilde{X}$
and
![]() $\widetilde{D}$
denote the inverse images of
$\widetilde{D}$
denote the inverse images of
![]() $X$
and
$X$
and
![]() $D$
, respectively, by the natural morphism
$D$
, respectively, by the natural morphism
![]() $\widetilde{\Sigma }_{V,\theta }\to Y$
. There exists a line bundle
$\widetilde{\Sigma }_{V,\theta }\to Y$
. There exists a line bundle
![]() $L_V$
on
$L_V$
on
![]() $\Sigma _{V,\theta }$
corresponding to
$\Sigma _{V,\theta }$
corresponding to
![]() $(V,\theta )$
. Let
$(V,\theta )$
. Let
![]() $\mathcal{P}_{\ast }\mathcal{L}_V$
be the filtered line bundle on
$\mathcal{P}_{\ast }\mathcal{L}_V$
be the filtered line bundle on
![]() $(\widetilde{\Sigma }_{V,\theta },\widetilde{D})$
corresponding to
$(\widetilde{\Sigma }_{V,\theta },\widetilde{D})$
corresponding to
![]() $(\mathcal{P}_{\ast }\mathcal{V},\theta )$
. There exists a Hermitian metric
$(\mathcal{P}_{\ast }\mathcal{V},\theta )$
. There exists a Hermitian metric
![]() $h_0$
of
$h_0$
of
![]() $L_{V}$
such that (i)
$L_{V}$
such that (i)
![]() $h_0$
is flat around any point of
$h_0$
is flat around any point of
![]() $\widetilde{D}$
, (ii)
$\widetilde{D}$
, (ii)
![]() $h_0$
is adapted to
$h_0$
is adapted to
![]() $\mathcal{P}_{\ast }\mathcal{L}_V$
and (iii)
$\mathcal{P}_{\ast }\mathcal{L}_V$
and (iii)
![]() $h_{0|{\partial } \widetilde{X}}$
induces
$h_{0|{\partial } \widetilde{X}}$
induces
![]() $h_{{\partial } X}$
. Let
$h_{{\partial } X}$
. Let
![]() $R(h_0)$
denote the curvature of the Chern connection of
$R(h_0)$
denote the curvature of the Chern connection of
![]() $(L_V,h_0)$
. It vanishes around
$(L_V,h_0)$
. It vanishes around
![]() $\widetilde{D}$
. There exists an
$\widetilde{D}$
. There exists an
![]() $\mathbb{R}$
-valued
$\mathbb{R}$
-valued
![]() $C^{\infty }$
-function
$C^{\infty }$
-function
![]() $\alpha$
on
$\alpha$
on
![]() $\widetilde{X}$
such that (i)
$\widetilde{X}$
such that (i)
![]() $\overline{\partial }{\partial }\alpha =R(h_0)_{|\widetilde{X}}$
and (ii)
$\overline{\partial }{\partial }\alpha =R(h_0)_{|\widetilde{X}}$
and (ii)
![]() $\alpha _{|{\partial } \widetilde{X}}=0$
. Then,
$\alpha _{|{\partial } \widetilde{X}}=0$
. Then,
![]() $h_1=e^{-\alpha }h_0$
is a flat metric of
$h_1=e^{-\alpha }h_0$
is a flat metric of
![]() $L_{V|\widetilde{X}}$
adapted to
$L_{V|\widetilde{X}}$
adapted to
![]() $\mathcal{P}_{\ast }\mathcal{L}_V$
such that
$\mathcal{P}_{\ast }\mathcal{L}_V$
such that
![]() $h_{1|{\partial } \widetilde{X}}=h_{0|{\partial } \widetilde{X}}$
. Let
$h_{1|{\partial } \widetilde{X}}=h_{0|{\partial } \widetilde{X}}$
. Let
![]() $h_2$
be the decoupled harmonic metric of
$h_2$
be the decoupled harmonic metric of
![]() $(V,\theta )_{|X\setminus D}$
corresponding to
$(V,\theta )_{|X\setminus D}$
corresponding to
![]() $h_1$
. It is adapted to
$h_1$
. It is adapted to
![]() $\mathcal{P}_{\ast }\mathcal{V}$
and it satisfies
$\mathcal{P}_{\ast }\mathcal{V}$
and it satisfies
![]() $h_{2|{\partial } X}=h_{{\partial } X}$
. By the uniqueness in Theorem2.8, we have
$h_{2|{\partial } X}=h_{{\partial } X}$
. By the uniqueness in Theorem2.8, we have
![]() $h=h_2$
.
$h=h_2$
.
6. Large-scale solutions with prescribed boundary value
6.1 Harmonic metrics of regular semisimple Higgs bundles on a punctured disc
6.1.1 General case
Let
![]() $U$
be a neighbourhood of
$U$
be a neighbourhood of
![]() $0$
in
$0$
in
![]() $\mathbb{C}$
. Let
$\mathbb{C}$
. Let
![]() $U_0$
be a relatively compact open neighbourhood of
$U_0$
be a relatively compact open neighbourhood of
![]() $0$
in
$0$
in
![]() $U$
with smooth boundary
$U$
with smooth boundary
![]() ${\partial } U_0$
. We set
${\partial } U_0$
. We set
![]() $U^{\ast }=U\setminus \{0\}$
and
$U^{\ast }=U\setminus \{0\}$
and
![]() $U_0^{\ast }=U_0\setminus \{0\}$
.
$U_0^{\ast }=U_0\setminus \{0\}$
.
Let
![]() $(\mathcal{P}_{\ast }\mathcal{V},\theta )$
be a good filtered Higgs bundle of rank
$(\mathcal{P}_{\ast }\mathcal{V},\theta )$
be a good filtered Higgs bundle of rank
![]() $r$
on
$r$
on
![]() $(U,0)$
such that
$(U,0)$
such that
![]() $(V,\theta ):=(\mathcal{V},\theta )_{|U^{\ast }}$
is regular semisimple. Let
$(V,\theta ):=(\mathcal{V},\theta )_{|U^{\ast }}$
is regular semisimple. Let
![]() $h_{{\partial } U_0}$
be a Hermitian metric of
$h_{{\partial } U_0}$
be a Hermitian metric of
![]() $V_{|{\partial } U_0}$
. According to Theorem2.8, for any
$V_{|{\partial } U_0}$
. According to Theorem2.8, for any
![]() $t\gt 0$
, there exists a unique harmonic metric
$t\gt 0$
, there exists a unique harmonic metric
![]() $h_t$
of
$h_t$
of
![]() $(V,t\theta )_{|U_0^{\ast }}$
such that
$(V,t\theta )_{|U_0^{\ast }}$
such that
![]() $h_{t|{\partial } U_0}=h_{{\partial } U_0}$
and that
$h_{t|{\partial } U_0}=h_{{\partial } U_0}$
and that
![]() $\mathcal{P}^{h_t}_{\ast }(V)=\mathcal{P}_{\ast }\mathcal{V}$
. Note that
$\mathcal{P}^{h_t}_{\ast }(V)=\mathcal{P}_{\ast }\mathcal{V}$
. Note that
![]() $\det (h_t)=\det (h_1)$
for any
$\det (h_t)=\det (h_1)$
for any
![]() $t\gt 0$
.
$t\gt 0$
.
Proposition 6.1.
Let
![]() $t(i)$
be any sequence of positive numbers such that
$t(i)$
be any sequence of positive numbers such that
![]() $t(i)\to \infty$
. Then, there exists a subsequence
$t(i)\to \infty$
. Then, there exists a subsequence
![]() $t'(j)$
such that the following hold:
$t'(j)$
such that the following hold:
-
–
 $t'(j)\to \infty$
;
$t'(j)\to \infty$
; -
– the sequence
 $h_{t'(j)}$
is convergent to a harmonic metric on any relatively compact open subset of
$h_{t'(j)}$
is convergent to a harmonic metric on any relatively compact open subset of
 $U_0^{\ast }$
in the
$U_0^{\ast }$
in the
 $C^{\infty }$
-sense.
$C^{\infty }$
-sense.
The limit
![]() $h_{\infty }$
is a decoupled harmonic metric of
$h_{\infty }$
is a decoupled harmonic metric of
![]() $(V,\theta )$
such that
$(V,\theta )$
such that
![]() $\mathcal{P}^{h_{\infty }}(V)=\mathcal{V}$
and that
$\mathcal{P}^{h_{\infty }}(V)=\mathcal{V}$
and that
![]() $\det (h_{\infty })=\det (h_1)$
.
$\det (h_{\infty })=\det (h_1)$
.
Proof.
By taking the pull back via a ramified covering map
![]() $\varphi _{\ell }$
as in §5.1.1, it is enough to consider the case where there exist meromorphic functions
$\varphi _{\ell }$
as in §5.1.1, it is enough to consider the case where there exist meromorphic functions
![]() $\gamma (1),\ldots, \gamma (r)$
on
$\gamma (1),\ldots, \gamma (r)$
on
![]() $(U,0)$
and a decomposition
$(U,0)$
and a decomposition
 \begin{align*} (\mathcal {V},\theta ) =\bigoplus _{i=1}^r (\mathcal {V}_{i},\gamma (i)\,dz). \end{align*}
\begin{align*} (\mathcal {V},\theta ) =\bigoplus _{i=1}^r (\mathcal {V}_{i},\gamma (i)\,dz). \end{align*}
Let
![]() $v_i$
be a frame of
$v_i$
be a frame of
![]() $\mathcal{V}_i$
on
$\mathcal{V}_i$
on
![]() $U$
such that
$U$
such that
![]() $v_i$
is a section of
$v_i$
is a section of
![]() $\mathcal{P}_{\lt 0}\mathcal{V}$
.
$\mathcal{P}_{\lt 0}\mathcal{V}$
.
Lemma 6.2.
There exists a constant
![]() $C\gt 0$
such that
$C\gt 0$
such that
![]() $h_{t}(v_i,v_i)\leqslant C$
for any
$h_{t}(v_i,v_i)\leqslant C$
for any
![]() $t\gt 0$
.
$t\gt 0$
.
Proof.
It is enough to consider the case where
![]() $\gamma (i)=0$
. We have
$\gamma (i)=0$
. We have
![]() $\theta (v_i)=0$
. Then, we have
$\theta (v_i)=0$
. Then, we have
![]() $-{\partial }_z{\partial }_{{\overline{z}}}|v_i|_{h_t}^2\leqslant 0$
on
$-{\partial }_z{\partial }_{{\overline{z}}}|v_i|_{h_t}^2\leqslant 0$
on
![]() $U_0^{\ast }$
(see a preliminary Weitzenböck formula in [Reference SimpsonSim90, Proof of Lemma 4.1]). Because
$U_0^{\ast }$
(see a preliminary Weitzenböck formula in [Reference SimpsonSim90, Proof of Lemma 4.1]). Because
![]() $v_i$
is a section of
$v_i$
is a section of
![]() $\mathcal{P}_{\lt 0}\mathcal{V}$
,
$\mathcal{P}_{\lt 0}\mathcal{V}$
,
![]() $|v_i|_{h_t}^2$
is bounded for each
$|v_i|_{h_t}^2$
is bounded for each
![]() $t$
. Hence,
$t$
. Hence,
![]() $|v_i|_{h_t}^2$
is subharmonic on
$|v_i|_{h_t}^2$
is subharmonic on
![]() $U_0$
. By the maximum principle, we obtain
$U_0$
. By the maximum principle, we obtain
![]() $|v_i|^2_{h_t} \leqslant \max _{{\partial } U_0}|v_i|_{h_t}^2 =\max _{{\partial } U_0}|v_i|_{h_1}^2$
.
$|v_i|^2_{h_t} \leqslant \max _{{\partial } U_0}|v_i|_{h_t}^2 =\max _{{\partial } U_0}|v_i|_{h_1}^2$
.
Let
![]() $\mathcal{V}^{\lor }={\mathcal Hom}_{\mathcal{O}_U}(\mathcal{V},\mathcal{O}_U(\ast 0))$
denote the dual of
$\mathcal{V}^{\lor }={\mathcal Hom}_{\mathcal{O}_U}(\mathcal{V},\mathcal{O}_U(\ast 0))$
denote the dual of
![]() $\mathcal{V}$
. We have the induced filtered bundle
$\mathcal{V}$
. We have the induced filtered bundle
![]() $\mathcal{P}_{\ast }(\mathcal{V}^{\lor })$
on
$\mathcal{P}_{\ast }(\mathcal{V}^{\lor })$
on
![]() $\mathcal{V}^{\lor }$
. We set
$\mathcal{V}^{\lor }$
. We set
![]() $(V^{\lor },\theta ^{\lor }) =(\mathcal{V}^{\lor },\theta ^{\lor })_{|U^{\ast }}$
. The induced harmonic metric
$(V^{\lor },\theta ^{\lor }) =(\mathcal{V}^{\lor },\theta ^{\lor })_{|U^{\ast }}$
. The induced harmonic metric
![]() $h_t^{\lor }$
of
$h_t^{\lor }$
of
![]() $(V^{\lor },t\theta ^{\lor })$
is adapted to
$(V^{\lor },t\theta ^{\lor })$
is adapted to
![]() $\mathcal{P}_{\ast }(\mathcal{V}^{\lor })$
.
$\mathcal{P}_{\ast }(\mathcal{V}^{\lor })$
.
There exists the induced decomposition
![]() $\mathcal{V}^{\lor } =\bigoplus _{i=1}^r\mathcal{V}_i^{\lor }$
. Let
$\mathcal{V}^{\lor } =\bigoplus _{i=1}^r\mathcal{V}_i^{\lor }$
. Let
![]() $v_i^{\lor }$
denote the section of
$v_i^{\lor }$
denote the section of
![]() $\mathcal{V}^{\lor }_i$
such that
$\mathcal{V}^{\lor }_i$
such that
![]() $v_i^{\lor }(v_i)=1$
. There exists
$v_i^{\lor }(v_i)=1$
. There exists
![]() $m(i)\in \mathbb{Z}_{\gt 0}$
such that
$m(i)\in \mathbb{Z}_{\gt 0}$
such that
![]() $z^{m(i)}v_i^{\lor }$
is a section of
$z^{m(i)}v_i^{\lor }$
is a section of
![]() $\mathcal{P}_{\lt 0}(\mathcal{V}^{\lor })$
. By Lemma 6.2, we obtain the following lemma.
$\mathcal{P}_{\lt 0}(\mathcal{V}^{\lor })$
. By Lemma 6.2, we obtain the following lemma.
Lemma 6.3.
There exists
![]() $C\gt 0$
such that
$C\gt 0$
such that
![]() $|z|^{2m(i)}h_t^{\lor }(v_i^{\lor },v_i^{\lor })\leqslant C$
for any
$|z|^{2m(i)}h_t^{\lor }(v_i^{\lor },v_i^{\lor })\leqslant C$
for any
![]() $t\gt 0$
.
$t\gt 0$
.
Let
![]() $s_t$
be the automorphism of
$s_t$
be the automorphism of
![]() $V_{|U_0^{\ast }}$
determined by
$V_{|U_0^{\ast }}$
determined by
![]() $h_t=h_1\cdot s_t$
. Let
$h_t=h_1\cdot s_t$
. Let
![]() $K$
be any relatively compact open subset of
$K$
be any relatively compact open subset of
![]() $U_0^{\ast }$
. By Lemmas 6.2 and 6.3, there exist
$U_0^{\ast }$
. By Lemmas 6.2 and 6.3, there exist
![]() $C_{K,1}\gt 0$
such that the following holds for any
$C_{K,1}\gt 0$
such that the following holds for any
![]() $t\gt 0$
:
$t\gt 0$
:
By a variant of Simpson’s main estimate (see [Reference MochizukiMoc16, Proposition 2.3]), there exist
![]() $t_{K,1},C_{K,2},C_{K,3}\gt 0$
such that the following holds for any
$t_{K,1},C_{K,2},C_{K,3}\gt 0$
such that the following holds for any
![]() $t\gt t_{K,1}$
and for any local sections
$t\gt t_{K,1}$
and for any local sections
![]() $u_{\beta (i)}$
and
$u_{\beta (i)}$
and
![]() $u_{\beta (j)}$
of
$u_{\beta (j)}$
of
![]() $V_{\beta (i)}$
and
$V_{\beta (i)}$
and
![]() $V_{\beta (j)}$
on
$V_{\beta (j)}$
on
![]() $K$
$K$
![]() $(i\neq j)$
:
$(i\neq j)$
:
There also exist
![]() $t_{K,2},C_{K,4},C_{K,5}\gt 0$
such that the following holds on
$t_{K,2},C_{K,4},C_{K,5}\gt 0$
such that the following holds on
![]() $K$
for any
$K$
for any
![]() $t\gt t_{K,2}$
(see [Reference MochizukiMoc16, Theorem 2.9]):
$t\gt t_{K,2}$
(see [Reference MochizukiMoc16, Theorem 2.9]):
By (43) and (45), it is standard to obtain the existence of a convergent subsequence
![]() $h_{t'(j)}$
. By (44) and (45), the limit is a decoupled harmonic metric. By Lemma 6.2, we obtain that
$h_{t'(j)}$
. By (44) and (45), the limit is a decoupled harmonic metric. By Lemma 6.2, we obtain that
![]() $h_{\infty }(v_i,v_i)\leqslant C$
. Hence,
$h_{\infty }(v_i,v_i)\leqslant C$
. Hence,
![]() $v_i$
are sections of
$v_i$
are sections of
![]() $\mathcal{P}^{h_{\infty }}(V)$
. This implies that
$\mathcal{P}^{h_{\infty }}(V)$
. This implies that
![]() $\mathcal{V}\subset \mathcal{P}^{h_{\infty }}(V)$
. Because both
$\mathcal{V}\subset \mathcal{P}^{h_{\infty }}(V)$
. Because both
![]() $\mathcal{V}$
and
$\mathcal{V}$
and
![]() $\mathcal{P}^{h_{\infty }}(V)$
are locally free
$\mathcal{P}^{h_{\infty }}(V)$
are locally free
![]() $\mathcal{O}_{U}(\ast 0)$
-modules, we obtain that
$\mathcal{O}_{U}(\ast 0)$
-modules, we obtain that
![]() $\mathcal{V}=\mathcal{P}^{h_{\infty }}(V)$
.
$\mathcal{V}=\mathcal{P}^{h_{\infty }}(V)$
.
Proposition 6.4.
Let
![]() $h_{\infty }$
denote the limit of a convergent subsequence in Proposition 6.1
. Suppose the following condition holds.
$h_{\infty }$
denote the limit of a convergent subsequence in Proposition 6.1
. Suppose the following condition holds.
-
– For every
 $z_0\in{\partial } U_0$
, the eigen decomposition of
$z_0\in{\partial } U_0$
, the eigen decomposition of
 $\theta$
at
$\theta$
at
 $z_0$
is orthogonal with respect to
$z_0$
is orthogonal with respect to
 $h_{{\partial } U_0}$
.
$h_{{\partial } U_0}$
.
Then,
![]() $h_{\infty |{\partial } U_0}=h_{{\partial } U_0}$
.
$h_{\infty |{\partial } U_0}=h_{{\partial } U_0}$
.
Proof.
Let
![]() $U_1$
be a relatively compact open neighbourhood of
$U_1$
be a relatively compact open neighbourhood of
![]() $0$
in
$0$
in
![]() $U_0$
with smooth boundary
$U_0$
with smooth boundary
![]() ${\partial } U_1$
. Because
${\partial } U_1$
. Because
![]() $h_{\infty }$
is a decoupled harmonic metric, the following condition is satisfied.
$h_{\infty }$
is a decoupled harmonic metric, the following condition is satisfied.
-
– For every
 $z_1\in{\partial } U_1$
, the eigen decomposition of
$z_1\in{\partial } U_1$
, the eigen decomposition of
 $\theta$
at
$\theta$
at
 $z_1$
is orthogonal with respect to
$z_1$
is orthogonal with respect to
 $h_{\infty }$
.
$h_{\infty }$
.
We set
![]() $A=U_0\setminus \overline{U_1}$
. By Proposition 5.37, there exists a decoupled harmonic metric
$A=U_0\setminus \overline{U_1}$
. By Proposition 5.37, there exists a decoupled harmonic metric
![]() $h^{(1)}$
of
$h^{(1)}$
of
![]() $(V,\overline{\partial }_V,\theta )_{|A}$
such that
$(V,\overline{\partial }_V,\theta )_{|A}$
such that
![]() $h^{(1)}_{|{\partial } U_0}=h_{{\partial } U_0}$
and
$h^{(1)}_{|{\partial } U_0}=h_{{\partial } U_0}$
and
![]() $h^{(1)}_{|{\partial } U_1}=h_{\infty |{\partial } U_1}$
. We note that
$h^{(1)}_{|{\partial } U_1}=h_{\infty |{\partial } U_1}$
. We note that
![]() $h^{(1)}$
is a harmonic metric of
$h^{(1)}$
is a harmonic metric of
![]() $(V,\overline{\partial }_V,t\theta )_{|A}$
for any
$(V,\overline{\partial }_V,t\theta )_{|A}$
for any
![]() $t\gt 0$
. We also note that
$t\gt 0$
. We also note that
![]() $\det (h^{(1)})=\det (h_1)_{|A}$
because
$\det (h^{(1)})=\det (h_1)_{|A}$
because
![]() $\det (h^{(1)})_{|{\partial } A}=\det (h_1)_{|{\partial } A}$
.
$\det (h^{(1)})_{|{\partial } A}=\det (h_1)_{|{\partial } A}$
.
Let
![]() $s_t$
be determined by
$s_t$
be determined by
![]() $h_t=h^{(1)}s_t$
on
$h_t=h^{(1)}s_t$
on
![]() $A$
. We have
$A$
. We have
![]() $-{\partial }_z{\partial }_{{\overline{z}}}{\mathop{\textrm{Tr}}\nolimits }(s_t)\leqslant 0$
. We have
$-{\partial }_z{\partial }_{{\overline{z}}}{\mathop{\textrm{Tr}}\nolimits }(s_t)\leqslant 0$
. We have
![]() $s_{t'(j)}\to{\mathop{\textrm{id}}\nolimits }$
on
$s_{t'(j)}\to{\mathop{\textrm{id}}\nolimits }$
on
![]() ${\partial } U_1$
and
${\partial } U_1$
and
![]() $s_{t'(j)}={\mathop{\textrm{id}}\nolimits }$
on
$s_{t'(j)}={\mathop{\textrm{id}}\nolimits }$
on
![]() ${\partial } U_0$
. Hence, we obtain
${\partial } U_0$
. Hence, we obtain
![]() $\bigl |{\mathop{\textrm{Tr}}\nolimits }(s_{t'(j)}-{\mathop{\textrm{id}}\nolimits }) \bigr |\to 0$
as
$\bigl |{\mathop{\textrm{Tr}}\nolimits }(s_{t'(j)}-{\mathop{\textrm{id}}\nolimits }) \bigr |\to 0$
as
![]() $t'(j)\to \infty$
. This implies the claim of the proposition.
$t'(j)\to \infty$
. This implies the claim of the proposition.
6.1.2 The irreducible case
Suppose that the spectral curve is irreducible, i.e.
![]() $\Sigma _{V,\theta }$
is connected. We obtain the decomposable filtered bundle
$\Sigma _{V,\theta }$
is connected. We obtain the decomposable filtered bundle
![]() $\mathcal{P}^{\star }_{\ast }(\mathcal{V})$
determined by
$\mathcal{P}^{\star }_{\ast }(\mathcal{V})$
determined by
![]() $\det (\mathcal{P}_{\ast }\mathcal{V})$
as in Proposition 5.13, which is not necessarily equal to
$\det (\mathcal{P}_{\ast }\mathcal{V})$
as in Proposition 5.13, which is not necessarily equal to
![]() $\mathcal{P}_{\ast }(\mathcal{V})$
.
$\mathcal{P}_{\ast }(\mathcal{V})$
.
Lemma 6.5.
Let
![]() $h_{\infty }$
denote the limit of a convergent subsequence in Proposition 6.1
. Then, we have
$h_{\infty }$
denote the limit of a convergent subsequence in Proposition 6.1
. Then, we have
![]() $\mathcal{P}^{h_{\infty }}_{\ast }(V) =\mathcal{P}^{\star }_{\ast }(\mathcal{V})$
.
$\mathcal{P}^{h_{\infty }}_{\ast }(V) =\mathcal{P}^{\star }_{\ast }(\mathcal{V})$
.
Proof.
We have
![]() $\mathcal{P}^{h_{\infty }}V=\mathcal{V}$
. Because
$\mathcal{P}^{h_{\infty }}V=\mathcal{V}$
. Because
![]() $h_{\infty }$
is a decoupled harmonic metric,
$h_{\infty }$
is a decoupled harmonic metric,
![]() $\mathcal{P}^{h_{\infty }}_{\ast }(\mathcal{V})$
is decomposable. Because
$\mathcal{P}^{h_{\infty }}_{\ast }(\mathcal{V})$
is decomposable. Because
![]() $\det (h_{\infty })=\det (h_1)$
, we obtain
$\det (h_{\infty })=\det (h_1)$
, we obtain
![]() $\det (\mathcal{P}^{h_{\infty }}_{\ast }V)=\det (\mathcal{P}_{\ast }\mathcal{V})$
. Then, the claim follows from the uniqueness of
$\det (\mathcal{P}^{h_{\infty }}_{\ast }V)=\det (\mathcal{P}_{\ast }\mathcal{V})$
. Then, the claim follows from the uniqueness of
![]() $\mathcal{P}^{\star }_{\ast }(\mathcal{V})$
.
$\mathcal{P}^{\star }_{\ast }(\mathcal{V})$
.
Let
![]() $h_0$
be any decoupled harmonic metric of
$h_0$
be any decoupled harmonic metric of
![]() $(V,\overline{\partial }_V,\theta )$
such that
$(V,\overline{\partial }_V,\theta )$
such that
![]() $\mathcal{P}^{h_0}(V)=\mathcal{V}$
and that
$\mathcal{P}^{h_0}(V)=\mathcal{V}$
and that
![]() $\det (h_0)$
is adapted to
$\det (h_0)$
is adapted to
![]() $\det (\mathcal{P}_{\ast }\mathcal{V})$
. By the argument in the proof of Lemma 6.5, we can prove
$\det (\mathcal{P}_{\ast }\mathcal{V})$
. By the argument in the proof of Lemma 6.5, we can prove
![]() $\mathcal{P}^{h_0}_{\ast }(V)=\mathcal{P}^{\star }_{\ast }(\mathcal{V})$
. Let
$\mathcal{P}^{h_0}_{\ast }(V)=\mathcal{P}^{\star }_{\ast }(\mathcal{V})$
. Let
![]() $h_t$
$h_t$
![]() $(t\gt 0)$
be the harmonic metrics of
$(t\gt 0)$
be the harmonic metrics of
![]() $(V,\overline{\partial }_V,t\theta )$
adapted to
$(V,\overline{\partial }_V,t\theta )$
adapted to
![]() $\mathcal{P}_{\ast }\mathcal{V}$
such that
$\mathcal{P}_{\ast }\mathcal{V}$
such that
![]() $h_{t|{\partial } U_0}=h_{0|{\partial } U_0}$
.
$h_{t|{\partial } U_0}=h_{0|{\partial } U_0}$
.
Proposition 6.6.
The sequence
![]() $h_t$
is convergent to
$h_t$
is convergent to
![]() $h_0$
as
$h_0$
as
![]() $t\to \infty$
in the
$t\to \infty$
in the
![]() $C^{\infty }$
-sense on any relatively compact open subset of
$C^{\infty }$
-sense on any relatively compact open subset of
![]() $U_0^{\ast }$
.
$U_0^{\ast }$
.
Proof.
Let
![]() $t_i$
be any subsequence such that
$t_i$
be any subsequence such that
![]() $t_i\to \infty$
and that
$t_i\to \infty$
and that
![]() $h_{t_i}$
is convergent. Let
$h_{t_i}$
is convergent. Let
![]() $h_{\infty }$
denote the limit. By Proposition 6.4, we have
$h_{\infty }$
denote the limit. By Proposition 6.4, we have
![]() $h_{\infty |{\partial } U_0}=h_{0|{\partial } U_0}$
. We also have
$h_{\infty |{\partial } U_0}=h_{0|{\partial } U_0}$
. We also have
![]() $\mathcal{P}_{\ast }^{h_{\infty }}(V) =\mathcal{P}^{\star }_{\ast }(\mathcal{V}) =\mathcal{P}_{\ast }^{h_0}(V)$
. Hence, we obtain
$\mathcal{P}_{\ast }^{h_{\infty }}(V) =\mathcal{P}^{\star }_{\ast }(\mathcal{V}) =\mathcal{P}_{\ast }^{h_0}(V)$
. Hence, we obtain
![]() $h_{\infty }=h_0$
. This implies that
$h_{\infty }=h_0$
. This implies that
![]() $h_t$
is convergent to
$h_t$
is convergent to
![]() $h_0$
as
$h_0$
as
![]() $t\to \infty$
.
$t\to \infty$
.
6.1.3 Symmetric case
We do not assume that the spectral curve is irreducible. Instead, suppose that there exists a perfect pairing
![]() $C$
of
$C$
of
![]() $(\mathcal{P}_{\ast }\mathcal{V},\theta )$
. There uniquely exists a decoupled harmonic metric
$(\mathcal{P}_{\ast }\mathcal{V},\theta )$
. There uniquely exists a decoupled harmonic metric
![]() $h^C$
of
$h^C$
of
![]() $(V,\theta )$
which is compatible with
$(V,\theta )$
which is compatible with
![]() $C$
. As in Lemma 5.23, we have
$C$
. As in Lemma 5.23, we have
![]() $\mathcal{P}^{h^C}_{\ast }(V)= \mathcal{P}^C_{\ast }\mathcal{V}$
.
$\mathcal{P}^{h^C}_{\ast }(V)= \mathcal{P}^C_{\ast }\mathcal{V}$
.
Suppose that
![]() $h_{{\partial } U_0}$
is compatible with
$h_{{\partial } U_0}$
is compatible with
![]() $C_{|{\partial } U_0}$
. Then,
$C_{|{\partial } U_0}$
. Then,
![]() $h_t$
$h_t$
![]() $(t\gt 0)$
are compatible with
$(t\gt 0)$
are compatible with
![]() $C$
by Corollary 2.9. Let
$C$
by Corollary 2.9. Let
![]() $s_t$
be determined by
$s_t$
be determined by
![]() $h_t=h^Cs_t$
. We note that
$h_t=h^Cs_t$
. We note that
![]() $\det (h_t)=\det (h_1)=\det (h^C)$
by the compatibility with
$\det (h_t)=\det (h_1)=\det (h^C)$
by the compatibility with
![]() $C$
. The following proposition is a special case of Corollary 3.5.
$C$
. The following proposition is a special case of Corollary 3.5.
Proposition 6.7.
If
![]() $h_{{\partial } U_0}$
is compatible with
$h_{{\partial } U_0}$
is compatible with
![]() $C_{|{\partial } U_0}$
, the sequence
$C_{|{\partial } U_0}$
, the sequence
![]() $h_t$
is convergent to
$h_t$
is convergent to
![]() $h^C$
in the
$h^C$
in the
![]() $C^{\infty }$
-sense on any relatively compact subset
$C^{\infty }$
-sense on any relatively compact subset
![]() $K$
of
$K$
of
![]() $U_0^{\ast }$
. Moreover, there exists
$U_0^{\ast }$
. Moreover, there exists
![]() $t(K)\gt 0$
such that the following holds for any
$t(K)\gt 0$
such that the following holds for any
![]() $\ell \geqslant 0$
.
$\ell \geqslant 0$
.
-
– There exists
 $C(K,\ell )$
and
$C(K,\ell )$
and
 $\epsilon (K,\ell )$
such that the norms of
$\epsilon (K,\ell )$
such that the norms of
 $s_t-{\mathop{\textrm{id}}\nolimits }$
$s_t-{\mathop{\textrm{id}}\nolimits }$
 $(t\geqslant t(K))$
and their derivatives up to order
$(t\geqslant t(K))$
and their derivatives up to order
 $\ell$
are dominated by
$\ell$
are dominated by
 $C(K,\ell )\exp (-\epsilon (K,\ell )t)$
.
$C(K,\ell )\exp (-\epsilon (K,\ell )t)$
.
Let us also consider the case where
![]() $h_{{\partial } U_0}$
is not necessarily compatible with
$h_{{\partial } U_0}$
is not necessarily compatible with
![]() $C_{|{\partial } U_0}$
, but
$C_{|{\partial } U_0}$
, but
![]() $\det (h_{{\partial } U_0})$
is compatible with
$\det (h_{{\partial } U_0})$
is compatible with
![]() $\det (C)_{|{\partial } U_0}$
. Because
$\det (C)_{|{\partial } U_0}$
. Because
![]() $\det (h_t)$
are compatible with
$\det (h_t)$
are compatible with
![]() $\det (C)$
on
$\det (C)$
on
![]() $U_0$
, we obtain
$U_0$
, we obtain
![]() $\det (h_t)=\det (h_1)=\det (h^C)$
.
$\det (h_t)=\det (h_1)=\det (h^C)$
.
Proposition 6.8.
Let
![]() $h_{t(i)}$
be a convergent subsequence, and let
$h_{t(i)}$
be a convergent subsequence, and let
![]() $h_{\infty }$
denote the limit as in Proposition 6.1
. Then,
$h_{\infty }$
denote the limit as in Proposition 6.1
. Then,
![]() $\mathcal{P}^{h_{\infty }}_{\ast }(V)=\mathcal{P}^C_{\ast }(\mathcal{V})$
.
$\mathcal{P}^{h_{\infty }}_{\ast }(V)=\mathcal{P}^C_{\ast }(\mathcal{V})$
.
Proof.
Let
![]() $h'_t$
$h'_t$
![]() $(t\gt 0)$
be harmonic metrics of
$(t\gt 0)$
be harmonic metrics of
![]() $(V,t\theta )$
which are compatible with
$(V,t\theta )$
which are compatible with
![]() $C$
, such that
$C$
, such that
![]() $\det (h'_t)=\det (h_1)$
. We have already proved that the sequence
$\det (h'_t)=\det (h_1)$
. We have already proved that the sequence
![]() $h'_t$
is convergent to
$h'_t$
is convergent to
![]() $h^C$
. We have
$h^C$
. We have
![]() $\det (h'_t)=\det (h_t)$
. Let
$\det (h'_t)=\det (h_t)$
. Let
![]() $s_t$
be the automorphism determined by
$s_t$
be the automorphism determined by
![]() $h_t=h_t's_t$
. Let
$h_t=h_t's_t$
. Let
![]() $s_{\infty }$
be determined by
$s_{\infty }$
be determined by
![]() $h_{\infty }=h^Cs_{\infty }$
. The sequence
$h_{\infty }=h^Cs_{\infty }$
. The sequence
![]() $s_t$
is convergent to
$s_t$
is convergent to
![]() $s_{\infty }$
. Because
$s_{\infty }$
. Because
![]() $\det (s_t)=1$
, we have
$\det (s_t)=1$
, we have
![]() $\det (s_{\infty })=1$
. Because
$\det (s_{\infty })=1$
. Because
![]() ${\mathop{\textrm{Tr}}\nolimits }(s_t)$
is subharmonic on
${\mathop{\textrm{Tr}}\nolimits }(s_t)$
is subharmonic on
![]() $U_0$
, we obtain that
$U_0$
, we obtain that
![]() $\max _{U_0}{\mathop{\textrm{Tr}}\nolimits }(s_t)= \max _{{\partial } U_0}{\mathop{\textrm{Tr}}\nolimits }(s_t) =\max _{{\partial } U_0}{\mathop{\textrm{Tr}}\nolimits }(s_1)$
. We obtain that
$\max _{U_0}{\mathop{\textrm{Tr}}\nolimits }(s_t)= \max _{{\partial } U_0}{\mathop{\textrm{Tr}}\nolimits }(s_t) =\max _{{\partial } U_0}{\mathop{\textrm{Tr}}\nolimits }(s_1)$
. We obtain that
![]() ${\mathop{\textrm{Tr}}\nolimits }(s_{\infty })$
is bounded. Then,
${\mathop{\textrm{Tr}}\nolimits }(s_{\infty })$
is bounded. Then,
![]() $s_{\infty }$
and
$s_{\infty }$
and
![]() $s_{\infty }^{-1}$
are bounded, and we obtain
$s_{\infty }^{-1}$
are bounded, and we obtain
![]() $\mathcal{P}^{h_{\infty }}(V)=\mathcal{P}^{C}_{\ast }(\mathcal{V})$
.
$\mathcal{P}^{h_{\infty }}(V)=\mathcal{P}^{C}_{\ast }(\mathcal{V})$
.
Suppose that for every
![]() $z_0\in{\partial } U_0$
the eigen decomposition of
$z_0\in{\partial } U_0$
the eigen decomposition of
![]() $\theta$
is orthogonal with respect to
$\theta$
is orthogonal with respect to
![]() $h_{{\partial } U_0}$
. There exists a decoupled harmonic metric
$h_{{\partial } U_0}$
. There exists a decoupled harmonic metric
![]() $\widetilde{h}$
of
$\widetilde{h}$
of
![]() $(V,\theta )$
such that
$(V,\theta )$
such that
![]() $\widetilde{h}_{|{\partial } U_0}=h_{{\partial } U_0}$
and
$\widetilde{h}_{|{\partial } U_0}=h_{{\partial } U_0}$
and
![]() $\mathcal{P}^{\widetilde{h}}_{\ast }(V)=\mathcal{P}^C_{\ast }(\mathcal{V})$
.
$\mathcal{P}^{\widetilde{h}}_{\ast }(V)=\mathcal{P}^C_{\ast }(\mathcal{V})$
.
Corollary 6.9.
The sequence
![]() $h_{t}$
is convergent to
$h_{t}$
is convergent to
![]() $\widetilde{h}$
.
$\widetilde{h}$
.
6.2 Local symmetrizability of Higgs bundles
Let
![]() $U$
be a simply connected open subset in
$U$
be a simply connected open subset in
![]() $\mathbb{C}$
. Let
$\mathbb{C}$
. Let
![]() $D$
be a finite subset of
$D$
be a finite subset of
![]() $U$
. Let
$U$
. Let
![]() $(E,\overline{\partial }_E,\theta )$
be a Higgs bundle on
$(E,\overline{\partial }_E,\theta )$
be a Higgs bundle on
![]() $U$
such that
$U$
such that
![]() $(V,\theta )=(E,\theta )_{|U\setminus D}$
is regular semisimple. Let
$(V,\theta )=(E,\theta )_{|U\setminus D}$
is regular semisimple. Let
![]() $\pi :\Sigma _{E,\theta }\to U$
denote the projection. Let
$\pi :\Sigma _{E,\theta }\to U$
denote the projection. Let
![]() $\rho :\widetilde{\Sigma }_{E,\theta }\to \Sigma _{E,\theta }$
denote the normalization of
$\rho :\widetilde{\Sigma }_{E,\theta }\to \Sigma _{E,\theta }$
denote the normalization of
![]() $\Sigma _{E,\theta }$
. We set
$\Sigma _{E,\theta }$
. We set
![]() $\widetilde{D}=(\pi \circ \rho )^{-1}(D)$
. We assume the following condition.
$\widetilde{D}=(\pi \circ \rho )^{-1}(D)$
. We assume the following condition.
-
– There exists a line bundle
 $L$
on
$L$
on
 $\widetilde{\Sigma }_{E,\theta }$
with an isomorphism
$\widetilde{\Sigma }_{E,\theta }$
with an isomorphism
 $(\pi \circ \rho )_{\ast }L\simeq E$
. Moreover, the Higgs field
$(\pi \circ \rho )_{\ast }L\simeq E$
. Moreover, the Higgs field
 $\theta$
of
$\theta$
of
 $E$
is induced by the
$E$
is induced by the
 $\mathcal{O}_{T^{\ast }U}$
-action on
$\mathcal{O}_{T^{\ast }U}$
-action on
 $\rho _{\ast }L$
.
$\rho _{\ast }L$
.
For any
![]() $P\in D$
, let
$P\in D$
, let
![]() $U_P$
be a simply connected neighbourhood of
$U_P$
be a simply connected neighbourhood of
![]() $P$
in
$P$
in
![]() $U$
such that
$U$
such that
![]() $U_P\cap D=\{P\}$
. We set
$U_P\cap D=\{P\}$
. We set
![]() $U_P^{\ast }=U_P\setminus \{P\}$
. There exists the decomposition
$U_P^{\ast }=U_P\setminus \{P\}$
. There exists the decomposition
such that the spectral curves of
![]() $(V_P^{[k]},\theta _P^{[k]})$
are connected. Because
$(V_P^{[k]},\theta _P^{[k]})$
are connected. Because
![]() $E\simeq (\pi \circ \rho )_{\ast }L$
, (46) extends to the decomposition
$E\simeq (\pi \circ \rho )_{\ast }L$
, (46) extends to the decomposition
Let
![]() $h$
be a decoupled harmonic metric of
$h$
be a decoupled harmonic metric of
![]() $(V,\theta )$
. The decomposition (46) is orthogonal with respect to
$(V,\theta )$
. The decomposition (46) is orthogonal with respect to
![]() $h$
. Let
$h$
. Let
![]() $h_P^{[k]}$
denote the restriction of
$h_P^{[k]}$
denote the restriction of
![]() $h$
to
$h$
to
![]() $V^{[k]}_P$
. We consider the following condition.
$V^{[k]}_P$
. We consider the following condition.
Condition 6.10.
![]() $\det (h^{[k]}_P)$
induces a flat metric of
$\det (h^{[k]}_P)$
induces a flat metric of
![]() $\det (E^{[k]}_P)$
, and
$\det (E^{[k]}_P)$
, and
![]() $\mathcal{P}^hV=E(\ast D)$
holds.
$\mathcal{P}^hV=E(\ast D)$
holds.
We shall prove the following proposition in §6.2.2 after the preliminary in §6.2.1.
Proposition 6.11.
Suppose that Condition 6.10 is satisfied at each
![]() $P\in D$
. Moreover, we assume that each connected component of
$P\in D$
. Moreover, we assume that each connected component of
![]() $\widetilde{\Sigma }_{E,\theta }$
is simply connected. Then, the following claims hold.
$\widetilde{\Sigma }_{E,\theta }$
is simply connected. Then, the following claims hold.
-
– There exists a non-degenerate symmetric pairing
 $C$
of
$C$
of
 $(E,\theta )$
such that
$(E,\theta )$
such that
 $C_{|U\setminus D}$
is compatible with
$C_{|U\setminus D}$
is compatible with
 $h$
.
$h$
. -
– Let
 $C'$
be a non-degenerate symmetric pairing of
$C'$
be a non-degenerate symmetric pairing of
 $(V,\theta )$
which is compatible with
$(V,\theta )$
which is compatible with
 $h$
. Then,
$h$
. Then,
 $C'$
induces a non-degenerate symmetric pairing of
$C'$
induces a non-degenerate symmetric pairing of
 $E$
.
$E$
.
Remark 6.12. If
![]() $\Sigma _{E,\theta }$
is a simply connected complex submanifold of
$\Sigma _{E,\theta }$
is a simply connected complex submanifold of
![]() $T^{\ast }U$
, we can apply Proposition 6.11 to
$T^{\ast }U$
, we can apply Proposition 6.11 to
![]() $(E,\theta )$
.
$(E,\theta )$
.
6.2.1 Special case
Let us study the case that
![]() $D=\{0\}$
, and that
$D=\{0\}$
, and that
![]() $\Sigma _{V,\theta }$
is connected. We set
$\Sigma _{V,\theta }$
is connected. We set
![]() $\mathcal{V}=E(\ast 0)$
. We use the notation in §5.1.1. By choosing an
$\mathcal{V}=E(\ast 0)$
. We use the notation in §5.1.1. By choosing an
![]() $r$
-th root of
$r$
-th root of
![]() $(\pi \circ \rho )^{\ast }(z)$
on
$(\pi \circ \rho )^{\ast }(z)$
on
![]() $\widetilde{\Sigma }_{E,\theta }$
, we obtain a holomorphic isomorphism
$\widetilde{\Sigma }_{E,\theta }$
, we obtain a holomorphic isomorphism
![]() $\psi :\widetilde{\Sigma }_{E,\theta }\to U^{(r)}$
such that
$\psi :\widetilde{\Sigma }_{E,\theta }\to U^{(r)}$
such that
![]() $\varphi _r\circ \psi =\pi \circ \rho$
. There exists the decomposition (41) on
$\varphi _r\circ \psi =\pi \circ \rho$
. There exists the decomposition (41) on
![]() $U^{(r)}$
. There exists the natural isomorphism
$U^{(r)}$
. There exists the natural isomorphism
![]() $\psi _{\ast }(L)(\ast 0)\simeq \mathcal{V}_{\beta (1)}$
. Let
$\psi _{\ast }(L)(\ast 0)\simeq \mathcal{V}_{\beta (1)}$
. Let
![]() $E_{\beta (1)}\subset \mathcal{V}_{\beta (1)}$
denote the image of
$E_{\beta (1)}\subset \mathcal{V}_{\beta (1)}$
denote the image of
![]() $L$
. We have
$L$
. We have
![]() $\varphi _{r\ast }(E_{\beta (1)})=E$
.
$\varphi _{r\ast }(E_{\beta (1)})=E$
.
Let
![]() $C_{\beta (1)}: \mathcal{V}_{\beta (1)}\otimes \mathcal{V}_{\beta (1)} \longrightarrow \mathcal{O}_{U^{(r)}}(\ast 0)$
be a non-degenerate symmetric pairing. There exists the morphism
$C_{\beta (1)}: \mathcal{V}_{\beta (1)}\otimes \mathcal{V}_{\beta (1)} \longrightarrow \mathcal{O}_{U^{(r)}}(\ast 0)$
be a non-degenerate symmetric pairing. There exists the morphism
![]() ${\mathop{\textrm{tr}}\nolimits }:\varphi _{r\ast }\mathcal{O}_{U^{(r)}}(\ast 0)\to \mathcal{O}_{U}(\ast 0)$
as in §2.2.2. We obtain the induced symmetric pairing
${\mathop{\textrm{tr}}\nolimits }:\varphi _{r\ast }\mathcal{O}_{U^{(r)}}(\ast 0)\to \mathcal{O}_{U}(\ast 0)$
as in §2.2.2. We obtain the induced symmetric pairing
![]() $\Psi (C_{\beta (1)})={\mathop{\textrm{tr}}\nolimits }\circ \varphi _{r\ast }(C_{\beta (1)})$
of
$\Psi (C_{\beta (1)})={\mathop{\textrm{tr}}\nolimits }\circ \varphi _{r\ast }(C_{\beta (1)})$
of
![]() $\mathcal{V}=\varphi _{r\ast }(\mathcal{V}_{\beta (1)})$
. There exists an integer
$\mathcal{V}=\varphi _{r\ast }(\mathcal{V}_{\beta (1)})$
. There exists an integer
![]() $k$
such that
$k$
such that
![]() $C_{\beta (1)}(E_{\beta (1)}\otimes E_{\beta (1)}) =\mathcal{O}_{U^{(r)}}(k\{0\})$
.
$C_{\beta (1)}(E_{\beta (1)}\otimes E_{\beta (1)}) =\mathcal{O}_{U^{(r)}}(k\{0\})$
.
Lemma 6.13. The pairing
![]() $\Psi (C_{\beta (1)})$
induces a symmetric pairing of
$\Psi (C_{\beta (1)})$
induces a symmetric pairing of
![]() $E$
if and only if
$E$
if and only if
![]() $k\leqslant r-1$
. The induced pairing is non-degenerate if and only if
$k\leqslant r-1$
. The induced pairing is non-degenerate if and only if
![]() $k=r-1$
.
$k=r-1$
.
Proof.
There exists a frame
![]() $v$
of
$v$
of
![]() $E_{\beta (1)}$
such that
$E_{\beta (1)}$
such that
![]() $C_{\beta (1)}(v,v)=\zeta ^{-k}$
. The tuple
$C_{\beta (1)}(v,v)=\zeta ^{-k}$
. The tuple
![]() $v,\zeta v,\ldots, \zeta ^{r-1}v$
induces a frame of
$v,\zeta v,\ldots, \zeta ^{r-1}v$
induces a frame of
![]() $E$
. Note that
$E$
. Note that
![]() ${\mathop{\textrm{tr}}\nolimits }(\zeta ^j)=0$
unless
${\mathop{\textrm{tr}}\nolimits }(\zeta ^j)=0$
unless
![]() $j\in r\mathbb{Z}$
. It is easy to see that
$j\in r\mathbb{Z}$
. It is easy to see that
are holomorphic at
![]() $0$
if and only if
$0$
if and only if
![]() $k\leqslant r-1$
, and that the induced pairing is non-degenerate at
$k\leqslant r-1$
, and that the induced pairing is non-degenerate at
![]() $0$
if and only if
$0$
if and only if
![]() $k=r-1$
.
$k=r-1$
.
Let
![]() $C_{0,\beta (1)}$
be a non-degenerate symmetric pairing of
$C_{0,\beta (1)}$
be a non-degenerate symmetric pairing of
![]() $\mathcal{V}_{\beta (1)}$
such that
$\mathcal{V}_{\beta (1)}$
such that
![]() $C_{0,\beta (1)}(E_{\beta (1)}\otimes E_{\beta (1)}) =\mathcal{O}_{U^{(r)}}((r-1)\{0\})$
. We set
$C_{0,\beta (1)}(E_{\beta (1)}\otimes E_{\beta (1)}) =\mathcal{O}_{U^{(r)}}((r-1)\{0\})$
. We set
![]() $C_{0}=\Psi (C_{0,\beta (1)})$
which is a non-degenerate symmetric pairing of
$C_{0}=\Psi (C_{0,\beta (1)})$
which is a non-degenerate symmetric pairing of
![]() $(E,\theta )$
. Let
$(E,\theta )$
. Let
![]() $h_0$
be a decoupled harmonic metric of
$h_0$
be a decoupled harmonic metric of
![]() $(V,\theta )$
compatible with
$(V,\theta )$
compatible with
![]() $C_0$
. We note that
$C_0$
. We note that
![]() $\det (h_0)$
is compatible with
$\det (h_0)$
is compatible with
![]() $\det (C_0)$
, and hence it induces a Hermitian metric of
$\det (C_0)$
, and hence it induces a Hermitian metric of
![]() $\det (E)$
.
$\det (E)$
.
Let
![]() $h_1$
be any decoupled harmonic metric of
$h_1$
be any decoupled harmonic metric of
![]() $(V,\theta )$
such that
$(V,\theta )$
such that
![]() $\mathcal{P}^{h_1}(V)=\mathcal{V}$
and that
$\mathcal{P}^{h_1}(V)=\mathcal{V}$
and that
![]() $\det (h_1)=\det (h_0)$
. According to Corollary 5.22, there exists a holomorphic function
$\det (h_1)=\det (h_0)$
. According to Corollary 5.22, there exists a holomorphic function
![]() $\gamma _1$
on
$\gamma _1$
on
![]() $U^{(r)}$
such that (i)
$U^{(r)}$
such that (i)
![]() $\varphi _r^{\ast }(h_1)_{|V_{\beta (1)}} =\exp (2{\mathop{\textrm{Re}}\nolimits }\gamma _1) \varphi _r^{\ast }(h_0)_{|V_{\beta (1)}}$
and (ii)
$\varphi _r^{\ast }(h_1)_{|V_{\beta (1)}} =\exp (2{\mathop{\textrm{Re}}\nolimits }\gamma _1) \varphi _r^{\ast }(h_0)_{|V_{\beta (1)}}$
and (ii)
![]() $\sum _{\sigma \in \mathop{\textrm{Gal}}\nolimits (r)} \sigma ^{\ast }\gamma _1=0$
. We set
$\sum _{\sigma \in \mathop{\textrm{Gal}}\nolimits (r)} \sigma ^{\ast }\gamma _1=0$
. We set
It is a non-degenerate symmetric pairing of
![]() $\mathcal{V}_{\beta (1)}$
satisfying
$\mathcal{V}_{\beta (1)}$
satisfying
![]() $C_{1,\beta (1)}(E_{\beta (1)}\otimes E_{\beta (1)}) =\mathcal{O}_{U^{(r)}}((r-1)\{0\})$
. We obtain a non-degenerate symmetric pairing
$C_{1,\beta (1)}(E_{\beta (1)}\otimes E_{\beta (1)}) =\mathcal{O}_{U^{(r)}}((r-1)\{0\})$
. We obtain a non-degenerate symmetric pairing
![]() $C_1=\Psi (C_{1,\beta (1)})$
of
$C_1=\Psi (C_{1,\beta (1)})$
of
![]() $(E,\theta )$
such that
$(E,\theta )$
such that
![]() $C_{1|U^{\ast }}$
is compatible with
$C_{1|U^{\ast }}$
is compatible with
![]() $h_1$
.
$h_1$
.
Let
![]() $h$
be any decoupled harmonic metric of
$h$
be any decoupled harmonic metric of
![]() $(V,\theta )$
such that
$(V,\theta )$
such that
![]() $\mathcal{P}^h(V)=\mathcal{V}$
and that
$\mathcal{P}^h(V)=\mathcal{V}$
and that
![]() $\det (h)$
induces a flat metric of
$\det (h)$
induces a flat metric of
![]() $\det (E)$
. There exists a holomorphic function
$\det (E)$
. There exists a holomorphic function
![]() $\gamma _2$
on
$\gamma _2$
on
![]() $U$
such that
$U$
such that
![]() $\det (h)=\exp (2r{\mathop{\textrm{Re}}\nolimits }(\gamma _2))\det (h_1)$
. Then,
$\det (h)=\exp (2r{\mathop{\textrm{Re}}\nolimits }(\gamma _2))\det (h_1)$
. Then,
![]() $C=\exp (2\gamma _2)C_1$
is compatible with
$C=\exp (2\gamma _2)C_1$
is compatible with
![]() $h$
, and it induces a non-degenerate symmetric pairing of
$h$
, and it induces a non-degenerate symmetric pairing of
![]() $E$
.
$E$
.
Lemma 6.14.
Let
![]() $C'$
be a non-degenerate symmetric pairing of
$C'$
be a non-degenerate symmetric pairing of
![]() $(V,\theta )$
compatible with
$(V,\theta )$
compatible with
![]() $h$
. Then,
$h$
. Then,
![]() $C'$
induces a non-degenerate symmetric pairing of
$C'$
induces a non-degenerate symmetric pairing of
![]() $E$
.
$E$
.
Proof.
There exist non-degenerate symmetric pairings
![]() $C_{\beta (1)}$
and
$C_{\beta (1)}$
and
![]() $C'_{\beta (1)}$
of
$C'_{\beta (1)}$
of
![]() $\mathcal{V}_{\beta (1)}$
such that
$\mathcal{V}_{\beta (1)}$
such that
![]() $\Psi (C_{\beta (1)})=C$
and
$\Psi (C_{\beta (1)})=C$
and
![]() $\Psi (C'_{\beta (1)})=C'$
, respectively. Because both
$\Psi (C'_{\beta (1)})=C'$
, respectively. Because both
![]() $C_{\beta (1)}$
and
$C_{\beta (1)}$
and
![]() $C'_{\beta (1)}$
are compatible with
$C'_{\beta (1)}$
are compatible with
![]() $\varphi _r^{\ast }(h)_{|V_{\beta (1)}}$
, there exists a constant
$\varphi _r^{\ast }(h)_{|V_{\beta (1)}}$
, there exists a constant
![]() $\alpha$
such that
$\alpha$
such that
![]() $|\alpha |=1$
and
$|\alpha |=1$
and
![]() $C'_{\beta (1)}=\alpha C_{\beta (1)}$
. Hence,
$C'_{\beta (1)}=\alpha C_{\beta (1)}$
. Hence,
![]() $C'_{\beta (1)}(E_{\beta (1)}\otimes E_{\beta (1)}) =\mathcal{O}_{U^{(r)}}((r-1)\{0\})$
, and hence
$C'_{\beta (1)}(E_{\beta (1)}\otimes E_{\beta (1)}) =\mathcal{O}_{U^{(r)}}((r-1)\{0\})$
, and hence
![]() $C'$
induces a non-degenerate symmetric pairing of
$C'$
induces a non-degenerate symmetric pairing of
![]() $E$
.
$E$
.
6.2.2 Proof of Proposition 6.11
It is enough to consider the case where
![]() $\Sigma _{V,\theta }$
is connected, which implies that
$\Sigma _{V,\theta }$
is connected, which implies that
![]() $\widetilde{\Sigma }_{E,\theta }$
is connected. Let
$\widetilde{\Sigma }_{E,\theta }$
is connected. Let
![]() $h_{L}$
denote the flat metric of
$h_{L}$
denote the flat metric of
![]() $L_{|\Sigma _{V,\theta }}$
corresponding to the decoupled harmonic metric
$L_{|\Sigma _{V,\theta }}$
corresponding to the decoupled harmonic metric
![]() $h$
. Let
$h$
. Let
![]() $P$
be any point of
$P$
be any point of
![]() $D$
. By Proposition 5.25, there exists a non-degenerate symmetric pairing of
$D$
. By Proposition 5.25, there exists a non-degenerate symmetric pairing of
![]() $V_{|U_P^{\ast }}$
which is compatible with
$V_{|U_P^{\ast }}$
which is compatible with
![]() $h_{|U_P^{\ast }}$
. There exists a non-degenerate symmetric pairing of
$h_{|U_P^{\ast }}$
. There exists a non-degenerate symmetric pairing of
![]() $L$
on
$L$
on
![]() $(\pi \circ \rho )^{-1}(U_P^{\ast })$
which is compatible with
$(\pi \circ \rho )^{-1}(U_P^{\ast })$
which is compatible with
![]() $h_L$
. Hence, the monodromy of the Chern connection of
$h_L$
. Hence, the monodromy of the Chern connection of
![]() $h_{L}$
around any point of
$h_{L}$
around any point of
![]() $\widetilde{D}$
is
$\widetilde{D}$
is
![]() $1$
or
$1$
or
![]() $-1$
. Because
$-1$
. Because
![]() $\widetilde{\Sigma }_{E,\theta }$
is simply connected, Lemma 2.7 implies that there exists a non-degenerate symmetric pairing
$\widetilde{\Sigma }_{E,\theta }$
is simply connected, Lemma 2.7 implies that there exists a non-degenerate symmetric pairing
![]() $C_{L}$
of
$C_{L}$
of
![]() $L_{|\Sigma _{V,\theta }}$
compatible with
$L_{|\Sigma _{V,\theta }}$
compatible with
![]() $h_{L}$
. It induces a non-degenerate symmetric pairing
$h_{L}$
. It induces a non-degenerate symmetric pairing
![]() $C$
of
$C$
of
![]() $(V,\theta )$
compatible with
$(V,\theta )$
compatible with
![]() $h$
. By Lemma 6.14,
$h$
. By Lemma 6.14,
![]() $C$
induces a non-degenerate symmetric pairing of
$C$
induces a non-degenerate symmetric pairing of
![]() $E$
. Thus, we obtain the first claim of Proposition 6.11. The second claim also follows from Lemma 6.14.
$E$
. Thus, we obtain the first claim of Proposition 6.11. The second claim also follows from Lemma 6.14.
6.3 A uniform estimate in the symmetric case
6.3.1 Setting
For
![]() $R\gt 0$
, we set
$R\gt 0$
, we set
![]() $B(R)=\bigl \{z\in \mathbb{C}\,\big |\,|z|\lt R\bigr \}$
. Let
$B(R)=\bigl \{z\in \mathbb{C}\,\big |\,|z|\lt R\bigr \}$
. Let
![]() $\mathcal{S}\subset \mathbb{C}^n$
be a connected open subset with a base point
$\mathcal{S}\subset \mathbb{C}^n$
be a connected open subset with a base point
![]() $x_0$
. Let
$x_0$
. Let
![]() $\mathcal{Z}_i$
$\mathcal{Z}_i$
![]() $(i=1,2)$
be an open subset of
$(i=1,2)$
be an open subset of
![]() $\mathcal{S}\times \mathbb{C}_{z_i}$
. For simplicity, we assume that
$\mathcal{S}\times \mathbb{C}_{z_i}$
. For simplicity, we assume that
![]() $\mathcal{Z}_2=\mathcal{S}\times B(2)$
. Let
$\mathcal{Z}_2=\mathcal{S}\times B(2)$
. Let
![]() $p_i:\mathcal{Z}_i\to \mathcal{S}$
denote the projections. We set
$p_i:\mathcal{Z}_i\to \mathcal{S}$
denote the projections. We set
![]() $T^{\ast }(\mathcal{Z}_2/\mathcal{S})=\mathcal{S}\times T^{\ast }B(2)$
. Let
$T^{\ast }(\mathcal{Z}_2/\mathcal{S})=\mathcal{S}\times T^{\ast }B(2)$
. Let
![]() $\pi _2:T^{\ast }(\mathcal{Z}_2/\mathcal{S})\to \mathcal{Z}_2$
denote the projection. Let
$\pi _2:T^{\ast }(\mathcal{Z}_2/\mathcal{S})\to \mathcal{Z}_2$
denote the projection. Let
![]() $\Phi _0:\mathcal{Z}_1\to T^{\ast }(\mathcal{Z}_2/\mathcal{S})$
be a holomorphic map such that
$\Phi _0:\mathcal{Z}_1\to T^{\ast }(\mathcal{Z}_2/\mathcal{S})$
be a holomorphic map such that
![]() $p_1=p_2\circ \pi _2\circ \Phi _0$
. We set
$p_1=p_2\circ \pi _2\circ \Phi _0$
. We set
![]() $\Phi _1:=\pi _2\circ \Phi _0:\mathcal{Z}_1\to \mathcal{Z}_2$
. We assume the following conditions:
$\Phi _1:=\pi _2\circ \Phi _0:\mathcal{Z}_1\to \mathcal{Z}_2$
. We assume the following conditions:
-
–
 $\Phi _1$
is proper and finite;
$\Phi _1$
is proper and finite; -
– there exists a complex analytic closed hypersurface
 $\mathcal{D}\subset \mathcal{S}\times B(R_1)\subset \mathcal{Z}_2$
for some
$\mathcal{D}\subset \mathcal{S}\times B(R_1)\subset \mathcal{Z}_2$
for some
 $0\lt R_1\lt 1$
such that (i) the induced map
$0\lt R_1\lt 1$
such that (i) the induced map
 $\mathcal{Z}_1\setminus \Phi _1^{-1}(\mathcal{D}) \longrightarrow \mathcal{Z}_2\setminus \mathcal{D}$
is a covering map, (ii)
$\mathcal{Z}_1\setminus \Phi _1^{-1}(\mathcal{D}) \longrightarrow \mathcal{Z}_2\setminus \mathcal{D}$
is a covering map, (ii)
 $\Phi _0$
induces an injection
$\Phi _0$
induces an injection
 $\mathcal{Z}_1\setminus \Phi _1^{-1}(\mathcal{D})\to T^{\ast }(\mathcal{Z}_2\setminus \mathcal{D})$
and (iii)
$\mathcal{Z}_1\setminus \Phi _1^{-1}(\mathcal{D})\to T^{\ast }(\mathcal{Z}_2\setminus \mathcal{D})$
and (iii)
 $\mathcal{D}\cap (\{x_0\}\times \mathbb{C})=\{(x_0,0)\}$
.
$\mathcal{D}\cap (\{x_0\}\times \mathbb{C})=\{(x_0,0)\}$
.
We set
![]() $r:=|\Phi _1^{-1}(P)|$
for any
$r:=|\Phi _1^{-1}(P)|$
for any
![]() $P\in \mathcal{Z}_2\setminus \mathcal{D}$
. We also set
$P\in \mathcal{Z}_2\setminus \mathcal{D}$
. We also set
![]() $\widetilde{\mathcal{D}}=\Phi _1^{-1}(\mathcal{D})$
.
$\widetilde{\mathcal{D}}=\Phi _1^{-1}(\mathcal{D})$
.
Lemma 6.15. The sheaf
![]() $\mathcal{E}=\Phi _{1\ast }(\mathcal{O}_{\mathcal{Z}_1})$
is a locally free
$\mathcal{E}=\Phi _{1\ast }(\mathcal{O}_{\mathcal{Z}_1})$
is a locally free
![]() $\mathcal{O}_{\mathcal{Z}_2}$
-module of rank
$\mathcal{O}_{\mathcal{Z}_2}$
-module of rank
![]() $r$
.
$r$
.
Proof.
By a change of local holomorphic coordinate system on
![]() $\mathcal{Z}_1$
, it is enough to consider the case where
$\mathcal{Z}_1$
, it is enough to consider the case where
![]() $\Phi _1^{\ast }(z_2)$
is expressed as a Weierstrass polynomial. Then, it is reduced to [Reference Grauert and RemmertGR84, Chapter 2, §4.2, Theorem].
$\Phi _1^{\ast }(z_2)$
is expressed as a Weierstrass polynomial. Then, it is reduced to [Reference Grauert and RemmertGR84, Chapter 2, §4.2, Theorem].
Note that
![]() $\mathcal{E}=\pi _{2\ast }(\Phi _{0\ast }\mathcal{O}_{\mathcal{Z}_1})$
is naturally a
$\mathcal{E}=\pi _{2\ast }(\Phi _{0\ast }\mathcal{O}_{\mathcal{Z}_1})$
is naturally a
![]() $\pi _{2\ast }(\mathcal{O}_{T^{\ast }(\mathcal{Z}_2/\mathcal{S})})$
-module. Hence, we obtain the relative Higgs field
$\pi _{2\ast }(\mathcal{O}_{T^{\ast }(\mathcal{Z}_2/\mathcal{S})})$
-module. Hence, we obtain the relative Higgs field
![]() $\theta :\mathcal{E}\to \mathcal{E}\otimes \Omega ^1_{\mathcal{Z}_2/\mathcal{S}}$
. The following lemma is clear by the construction.
$\theta :\mathcal{E}\to \mathcal{E}\otimes \Omega ^1_{\mathcal{Z}_2/\mathcal{S}}$
. The following lemma is clear by the construction.
Lemma 6.16.
For any
![]() $P\in \mathcal{Z}_2\setminus \mathcal{D}$
, there exist a neighbourhood
$P\in \mathcal{Z}_2\setminus \mathcal{D}$
, there exist a neighbourhood
![]() $\mathcal{U}$
of
$\mathcal{U}$
of
![]() $P$
in
$P$
in
![]() $\mathcal{Z}_2\setminus \mathcal{D}$
and a decomposition
$\mathcal{Z}_2\setminus \mathcal{D}$
and a decomposition
 \begin{align} (\mathcal{E},\theta )_{|\mathcal{U}} =\bigoplus _{i=1}^{r} (\mathcal{E}_{P,i},\theta _{P,i}), \end{align}
\begin{align} (\mathcal{E},\theta )_{|\mathcal{U}} =\bigoplus _{i=1}^{r} (\mathcal{E}_{P,i},\theta _{P,i}), \end{align}
where
![]() $\mathop{\textrm{rank}}\nolimits \mathcal{E}_{P,i}=1$
, and
$\mathop{\textrm{rank}}\nolimits \mathcal{E}_{P,i}=1$
, and
![]() $\theta _{P,i}-\theta _{P,j}$
$\theta _{P,i}-\theta _{P,j}$
![]() $(i\neq j)$
are nowhere vanishing.
$(i\neq j)$
are nowhere vanishing.
For any
![]() $x\in \mathcal{S}$
, we set
$x\in \mathcal{S}$
, we set
![]() $\mathcal{Z}_{i,x}=\mathcal{Z}_i\cap (\{x\}\times \mathbb{C})$
,
$\mathcal{Z}_{i,x}=\mathcal{Z}_i\cap (\{x\}\times \mathbb{C})$
,
![]() $\widetilde{\mathcal{D}}_x=\widetilde{\mathcal{D}}\cap (\{x\}\times \mathbb{C})$
and
$\widetilde{\mathcal{D}}_x=\widetilde{\mathcal{D}}\cap (\{x\}\times \mathbb{C})$
and
![]() $\mathcal{D}_x=\mathcal{D}\cap (\{x\}\times \mathbb{C})$
. Note that
$\mathcal{D}_x=\mathcal{D}\cap (\{x\}\times \mathbb{C})$
. Note that
![]() $\mathcal{Z}_{2,x}=B(2)$
for any
$\mathcal{Z}_{2,x}=B(2)$
for any
![]() $x\in \mathcal{S}$
. Let
$x\in \mathcal{S}$
. Let
![]() $\iota _x:\mathcal{Z}_{2,x}\to \mathcal{Z}_2$
denote the inclusion. We obtain the Higgs bundles
$\iota _x:\mathcal{Z}_{2,x}\to \mathcal{Z}_2$
denote the inclusion. We obtain the Higgs bundles
![]() $(\mathcal{E}_x,\theta _x):=\iota _x^{\ast }(\mathcal{E},\theta )$
on
$(\mathcal{E}_x,\theta _x):=\iota _x^{\ast }(\mathcal{E},\theta )$
on
![]() $\mathcal{Z}_{2,x}$
which is regular semisimple outside
$\mathcal{Z}_{2,x}$
which is regular semisimple outside
![]() $\mathcal{D}_{x}$
.
$\mathcal{D}_{x}$
.
6.3.2 A uniform estimate in the symmetric case
Let
![]() $h^{\circ }_{x}$
$h^{\circ }_{x}$
![]() $(x\in \mathcal{S})$
be decoupled harmonic metrics of
$(x\in \mathcal{S})$
be decoupled harmonic metrics of
![]() $(\mathcal{E}_{x},\theta _{x}) _{|B(2)\setminus \mathcal{D}_{x}}$
such that they induce a
$(\mathcal{E}_{x},\theta _{x}) _{|B(2)\setminus \mathcal{D}_{x}}$
such that they induce a
![]() $C^{\infty }$
-metric of
$C^{\infty }$
-metric of
![]() $\mathcal{E}_{|\mathcal{Z}_2\setminus \mathcal{D}}$
. Assume the following.
$\mathcal{E}_{|\mathcal{Z}_2\setminus \mathcal{D}}$
. Assume the following.
Condition 6.17.
For each
![]() $(x,P)\in \mathcal{D}$
, Condition 6.10 is satisfied for
$(x,P)\in \mathcal{D}$
, Condition 6.10 is satisfied for
![]() $(\mathcal{E}_x,\theta _x,h^{\circ }_x)$
at
$(\mathcal{E}_x,\theta _x,h^{\circ }_x)$
at
![]() $P$
.
$P$
.
Let
![]() $h_{x,t}$
be harmonic metrics of
$h_{x,t}$
be harmonic metrics of
![]() $(\mathcal{E}_x,t\theta _x)_{|B(1)}$
such that
$(\mathcal{E}_x,t\theta _x)_{|B(1)}$
such that
![]() $h_{x,t|{\partial } B(1)}=h^{\circ }_{x|{\partial } B(1)}$
. Let
$h_{x,t|{\partial } B(1)}=h^{\circ }_{x|{\partial } B(1)}$
. Let
![]() $s_{x,t}$
be the automorphism of
$s_{x,t}$
be the automorphism of
![]() $\mathcal{E}_{x|B(1)\setminus \mathcal{D}_x}$
determined by
$\mathcal{E}_{x|B(1)\setminus \mathcal{D}_x}$
determined by
![]() $h_{x,t}=h^{\circ }_{x}\cdot s_{x,t}$
.
$h_{x,t}=h^{\circ }_{x}\cdot s_{x,t}$
.
Proposition 6.18.
Let
![]() $R_1\lt R_2\lt 1$
. Let
$R_1\lt R_2\lt 1$
. Let
![]() $\mathcal{S}'$
be a relatively compact open subset of
$\mathcal{S}'$
be a relatively compact open subset of
![]() $\mathcal{S}$
. Then, there exists
$\mathcal{S}$
. Then, there exists
![]() $t_0\gt 0$
such that the following hold.
$t_0\gt 0$
such that the following hold.
-
– For any
 $\ell \in \mathbb{Z}_{\geqslant 0}$
, there exist positive constants
$\ell \in \mathbb{Z}_{\geqslant 0}$
, there exist positive constants
 $C(\ell )$
and
$C(\ell )$
and
 $\epsilon (\ell )$
such that
for any
$\epsilon (\ell )$
such that
for any \begin{align*} \bigl | (s_{x,t}-{\mathop {\textrm {id}}\nolimits })_{|B(R_2)\setminus B(R_1)}\bigr |_{L_{\ell }^2} \leqslant C(\ell )\exp (-\epsilon (\ell ) t) \end{align*}
\begin{align*} \bigl | (s_{x,t}-{\mathop {\textrm {id}}\nolimits })_{|B(R_2)\setminus B(R_1)}\bigr |_{L_{\ell }^2} \leqslant C(\ell )\exp (-\epsilon (\ell ) t) \end{align*}
 $x\in \mathcal{S}'$
and any
$x\in \mathcal{S}'$
and any
 $t\geqslant t_0$
. Here, we consider the
$t\geqslant t_0$
. Here, we consider the
 $L_{\ell }^2$
-norms with respect to
$L_{\ell }^2$
-norms with respect to
 $h^{\circ }_x$
and the standard Euclidean metric
$h^{\circ }_x$
and the standard Euclidean metric
 $dz_2\,d{\overline{z}}_2$
.
$dz_2\,d{\overline{z}}_2$
.
Proof.
For
![]() $0\lt R\leqslant 2$
, we set
$0\lt R\leqslant 2$
, we set
![]() $\mathcal{Z}_{1,x}(R):=\Phi _1^{-1}(\{x\}\times B(R)) \subset \mathcal{Z}_{1,x}$
.
$\mathcal{Z}_{1,x}(R):=\Phi _1^{-1}(\{x\}\times B(R)) \subset \mathcal{Z}_{1,x}$
.
Lemma 6.19.
If
![]() $R_1\lt R\leqslant 2$
, each connected component of
$R_1\lt R\leqslant 2$
, each connected component of
![]() $\mathcal{Z}_{1,x}(R)$
is diffeomorphic to a two
$\mathcal{Z}_{1,x}(R)$
is diffeomorphic to a two
![]() $2$
-dimensional disc.
$2$
-dimensional disc.
Proof.
Let us consider the case
![]() $R_1\lt R\lt 2$
. We set
$R_1\lt R\lt 2$
. We set
![]() $\mathcal{Z}_{1}(R):=\Phi _1^{-1}(\mathcal{S}\times B(R)) \subset \mathcal{Z}$
. The closure
$\mathcal{Z}_{1}(R):=\Phi _1^{-1}(\mathcal{S}\times B(R)) \subset \mathcal{Z}$
. The closure
![]() $\overline{\mathcal{Z}}_1(R)$
of
$\overline{\mathcal{Z}}_1(R)$
of
![]() $\mathcal{Z}_1(R)$
is a
$\mathcal{Z}_1(R)$
is a
![]() $C^{\infty }$
-manifold with smooth boundary. The projection
$C^{\infty }$
-manifold with smooth boundary. The projection
![]() $\overline{\mathcal{Z}}_{1}(R)\to \mathcal{S}$
is submersive and proper. Each connected component of
$\overline{\mathcal{Z}}_{1}(R)\to \mathcal{S}$
is submersive and proper. Each connected component of
![]() $\mathcal{Z}_{1,x_0}(R)$
is diffeomorphic to a disc. Because
$\mathcal{Z}_{1,x_0}(R)$
is diffeomorphic to a disc. Because
![]() $\mathcal{S}$
is connected, we obtain that each connected component of
$\mathcal{S}$
is connected, we obtain that each connected component of
![]() $\mathcal{Z}_{1,x}(R)$
is diffeomorphic to a disc. For
$\mathcal{Z}_{1,x}(R)$
is diffeomorphic to a disc. For
![]() $R_1\lt R\lt 2$
, there exists a diffeomorphism
$R_1\lt R\lt 2$
, there exists a diffeomorphism
![]() $\rho _R:B(R)\simeq B(2)$
whose restriction to
$\rho _R:B(R)\simeq B(2)$
whose restriction to
![]() $B(R_1)$
is the identity. We can construct a diffeomorphism
$B(R_1)$
is the identity. We can construct a diffeomorphism
![]() $\mathcal{Z}_{1,x}(R)\simeq \mathcal{Z}_{1,x}(2)$
by lifting
$\mathcal{Z}_{1,x}(R)\simeq \mathcal{Z}_{1,x}(2)$
by lifting
![]() $\rho _R$
.
$\rho _R$
.
Lemma 6.20.
There exist holomorphic non-degenerate symmetric pairings
![]() $C_x$
$C_x$
![]() $(x\in \mathcal{S})$
of
$(x\in \mathcal{S})$
of
![]() $(\mathcal{E}_{x},\theta _{x})$
such that the restrictions
$(\mathcal{E}_{x},\theta _{x})$
such that the restrictions
![]() $C_{x|B(1)\setminus \mathcal{D}_{x}}$
are compatible with
$C_{x|B(1)\setminus \mathcal{D}_{x}}$
are compatible with
![]() $h^{\circ }_x$
and continuous with respect to
$h^{\circ }_x$
and continuous with respect to
![]() $x$
.
$x$
.
Proof.
Let
![]() $h^{\circ }_{0,x}$
denote the flat metric of
$h^{\circ }_{0,x}$
denote the flat metric of
![]() $\mathcal{O}_{\mathcal{Z}_{1,x}\setminus \widetilde{\mathcal{D}}_{x}}$
corresponding to
$\mathcal{O}_{\mathcal{Z}_{1,x}\setminus \widetilde{\mathcal{D}}_{x}}$
corresponding to
![]() $h^{\circ }_x$
, which are continuous with respect to
$h^{\circ }_x$
, which are continuous with respect to
![]() $x$
. Let
$x$
. Let
![]() $\nabla ^{\circ }_{0,x}$
denote the Chern connection. They are flat connections, and continuous with respect to
$\nabla ^{\circ }_{0,x}$
denote the Chern connection. They are flat connections, and continuous with respect to
![]() $x$
.
$x$
.
By Proposition 6.11 and Lemma 6.19, for each
![]() $x\in \mathcal{S}$
, there exists a holomorphic non-degenerate symmetric pairing
$x\in \mathcal{S}$
, there exists a holomorphic non-degenerate symmetric pairing
![]() $C'_x$
of
$C'_x$
of
![]() $(\mathcal{E}_{x},\theta _{x})$
such that the restriction
$(\mathcal{E}_{x},\theta _{x})$
such that the restriction
![]() $(C'_{x})_{|B(1)\setminus \mathcal{D}_{x}}$
is compatible with
$(C'_{x})_{|B(1)\setminus \mathcal{D}_{x}}$
is compatible with
![]() $h^{\circ }_x$
. Let
$h^{\circ }_x$
. Let
![]() $C'_{0,x}$
denote the holomorphic non-degenerate symmetric bilinear form of
$C'_{0,x}$
denote the holomorphic non-degenerate symmetric bilinear form of
![]() $\mathcal{O}_{\mathcal{Z}_{1,x}\setminus \widetilde{\mathcal{D}}_{x}}$
corresponding to
$\mathcal{O}_{\mathcal{Z}_{1,x}\setminus \widetilde{\mathcal{D}}_{x}}$
corresponding to
![]() $C'_x$
, which is compatible with
$C'_x$
, which is compatible with
![]() $h^{\circ }_{0,x}$
.
$h^{\circ }_{0,x}$
.
Let
![]() $z_1\in B(1)\setminus B(R_1)$
. There exists a continuous family of non-degenerate symmetric pairings
$z_1\in B(1)\setminus B(R_1)$
. There exists a continuous family of non-degenerate symmetric pairings
![]() $C^{\circ }_{0,(x,z_1)}$
of the vector space
$C^{\circ }_{0,(x,z_1)}$
of the vector space
![]() $\mathcal{O}_{\mathcal{Z}_1|(x,z_1)}$
which are compatible with
$\mathcal{O}_{\mathcal{Z}_1|(x,z_1)}$
which are compatible with
![]() $(h^{\circ }_{0,x})_{|z_1}$
. We obtain
$(h^{\circ }_{0,x})_{|z_1}$
. We obtain
![]() $\alpha _x\in \mathbb{C}^{\ast }$
determined by
$\alpha _x\in \mathbb{C}^{\ast }$
determined by
![]() $C^{\circ }_{0,(x,z_1)}=\alpha _x (C'_{0,x})_{|z_1}$
. We set
$C^{\circ }_{0,(x,z_1)}=\alpha _x (C'_{0,x})_{|z_1}$
. We set
![]() $C_{0,x}=\alpha _x C'_{0,x}$
. Because
$C_{0,x}=\alpha _x C'_{0,x}$
. Because
![]() $C_{0,x}$
are
$C_{0,x}$
are
![]() $\nabla ^{\circ }_{0,x}$
-flat, they are continuous with respect to
$\nabla ^{\circ }_{0,x}$
-flat, they are continuous with respect to
![]() $x$
. Let
$x$
. Let
![]() $C_{x}$
denote the non-degenerate symmetric pairing of
$C_{x}$
denote the non-degenerate symmetric pairing of
![]() $(\mathcal{E}_x,\theta _x)$
corresponding to
$(\mathcal{E}_x,\theta _x)$
corresponding to
![]() $C_{0,x}$
. (See Proposition 6.11.) Then, they satisfy the desired condition.
$C_{0,x}$
. (See Proposition 6.11.) Then, they satisfy the desired condition.
Because
![]() $h_{t,x|{\partial } B(1)}=h^{\circ }_{x|{\partial } B(1)}$
are compatible with
$h_{t,x|{\partial } B(1)}=h^{\circ }_{x|{\partial } B(1)}$
are compatible with
![]() $C_{x|{\partial } B(1)}$
, we obtain that
$C_{x|{\partial } B(1)}$
, we obtain that
![]() $h_{t,x}$
are compatible with
$h_{t,x}$
are compatible with
![]() $C_x$
. Then, the claim of Proposition 6.18 follows from Theorem3.4.
$C_x$
. Then, the claim of Proposition 6.18 follows from Theorem3.4.
We also obtain the following proposition from Theorem3.4, as in the proof of Proposition 6.18.
Proposition 6.21.
Let
![]() $R_1\lt R_2\lt 2$
. Let
$R_1\lt R_2\lt 2$
. Let
![]() $\mathcal{S}'$
be a relatively compact open subset of
$\mathcal{S}'$
be a relatively compact open subset of
![]() $\mathcal{S}$
. There exists
$\mathcal{S}$
. There exists
![]() $t_0\gt 0$
such that the following holds.
$t_0\gt 0$
such that the following holds.
-
– Let
 $h'_{x,t}$
be any harmonic metrics of
$h'_{x,t}$
be any harmonic metrics of
 $(\mathcal{E}_x,t\theta _x)$
$(\mathcal{E}_x,t\theta _x)$
 $(x\in \mathcal{S}')$
compatible with
$(x\in \mathcal{S}')$
compatible with
 $C^{\circ }_x$
. Let
$C^{\circ }_x$
. Let
 $s'_{x,t}$
be determined by
$s'_{x,t}$
be determined by
 $h'_{x,t}=h^{\circ }_x\cdot s'_{x,t}$
. Then, for any
$h'_{x,t}=h^{\circ }_x\cdot s'_{x,t}$
. Then, for any
 $\ell \in \mathbb{Z}_{\geqslant 0}$
, there exist positive constants
$\ell \in \mathbb{Z}_{\geqslant 0}$
, there exist positive constants
 $C(\ell )$
and
$C(\ell )$
and
 $\epsilon (\ell )$
such that
for any
$\epsilon (\ell )$
such that
for any \begin{align*} \bigl | (s'_{x,t}-{\mathop {\textrm {id}}\nolimits })_{|B(R_2)\setminus B(R_1)}\bigr |_{L_{\ell }^2} \leqslant C(\ell )\exp (-\epsilon (\ell ) t), \end{align*}
\begin{align*} \bigl | (s'_{x,t}-{\mathop {\textrm {id}}\nolimits })_{|B(R_2)\setminus B(R_1)}\bigr |_{L_{\ell }^2} \leqslant C(\ell )\exp (-\epsilon (\ell ) t), \end{align*}
 $t\geqslant t_0$
.
$t\geqslant t_0$
.
6.3.3 Examples of non-degenerate symmetric pairings and decoupled harmonic metrics
We obtain a holomorphic function
![]() $G={\partial }_{z_1}(\Phi _1^{\ast }(z_2))$
. We have
$G={\partial }_{z_1}(\Phi _1^{\ast }(z_2))$
. We have
![]() $G^{-1}(0)\subset \widetilde{\mathcal{D}}$
. We define the symmetric product
$G^{-1}(0)\subset \widetilde{\mathcal{D}}$
. We define the symmetric product
![]() $C_0:\mathcal{O}_{\mathcal{Z}_1}\otimes \mathcal{O}_{\mathcal{Z}_1} \longrightarrow G^{-1}\mathcal{O}_{\mathcal{Z}_1}$
by
$C_0:\mathcal{O}_{\mathcal{Z}_1}\otimes \mathcal{O}_{\mathcal{Z}_1} \longrightarrow G^{-1}\mathcal{O}_{\mathcal{Z}_1}$
by
We obtain the following lemma by using Lemma 6.13.
Lemma 6.22. The pairing
![]() $C_0$
induces a non-degenerate symmetric pairing
$C_0$
induces a non-degenerate symmetric pairing
![]() $C_1$
of
$C_1$
of
![]() $\mathcal{E}$
, which induces a non-degenerate symmetric pairing of
$\mathcal{E}$
, which induces a non-degenerate symmetric pairing of
![]() $(\mathcal{E}_x,\theta _x)$
for any
$(\mathcal{E}_x,\theta _x)$
for any
![]() $x\in \mathcal{S}$
.
$x\in \mathcal{S}$
.
Let
![]() $h_0$
be the flat metric of
$h_0$
be the flat metric of
![]() $\mathcal{O}_{\mathcal{Z}_1\setminus \widetilde{\mathcal{D}}}$
defined as follows:
$\mathcal{O}_{\mathcal{Z}_1\setminus \widetilde{\mathcal{D}}}$
defined as follows:
Lemma 6.23. The metric
![]() $h_0$
induces a flat metric
$h_0$
induces a flat metric
![]() $h_1$
of
$h_1$
of
![]() $\mathcal{E}_{|\mathcal{Z}_2\setminus \mathcal{D}}$
. For each
$\mathcal{E}_{|\mathcal{Z}_2\setminus \mathcal{D}}$
. For each
![]() $x\in \mathcal{S}$
, the induced metric
$x\in \mathcal{S}$
, the induced metric
![]() $h_{1,x}$
of
$h_{1,x}$
of
![]() $(\mathcal{E}_x,\theta _x)_{|\mathcal{Z}_{2,x}\setminus \mathcal{D}_{x}}$
is a decoupled harmonic metric such that
$(\mathcal{E}_x,\theta _x)_{|\mathcal{Z}_{2,x}\setminus \mathcal{D}_{x}}$
is a decoupled harmonic metric such that
![]() $\det (h_{1,x})$
induces a flat metric of
$\det (h_{1,x})$
induces a flat metric of
![]() $\det (\mathcal{E}_{x})$
for each
$\det (\mathcal{E}_{x})$
for each
![]() $x\in \mathcal{S}$
.
$x\in \mathcal{S}$
.
Remark 6.24. We shall use
![]() $h_0$
in §7.3.
$h_0$
in §7.3.
7. Large-scale solutions on compact Riemann surfaces
7.1 Convergence in the locally irreducible case
7.1.1 Statement
Let
![]() $X$
be a compact Riemann surface. Let
$X$
be a compact Riemann surface. Let
![]() $\pi :T^{\ast }X\to X$
denote the projection. For any
$\pi :T^{\ast }X\to X$
denote the projection. For any
![]() $A\subset T^{\ast }X$
, the induced map
$A\subset T^{\ast }X$
, the induced map
![]() $A\to X$
is also denoted by
$A\to X$
is also denoted by
![]() $\pi$
. Let
$\pi$
. Let
![]() $D\subset X$
be a finite subset.
$D\subset X$
be a finite subset.
Let
![]() $(\mathcal{P}_{\ast }\mathcal{V},\theta )$
be a good filtered Higgs bundle of degree
$(\mathcal{P}_{\ast }\mathcal{V},\theta )$
be a good filtered Higgs bundle of degree
![]() $0$
on
$0$
on
![]() $(X,D)$
. We obtain the Higgs bundle
$(X,D)$
. We obtain the Higgs bundle
![]() $(V,\theta )=(\mathcal{V},\theta )_{|X\setminus D}$
. We assume the following.
$(V,\theta )=(\mathcal{V},\theta )_{|X\setminus D}$
. We assume the following.
Condition 7.1. The Higgs bundle
![]() $(V,\theta )$
is a regular semisimple Higgs bundle on
$(V,\theta )$
is a regular semisimple Higgs bundle on
![]() $X\setminus D$
.
$X\setminus D$
.
Remark 7.2. If
![]() $(V,\theta )$
is generically regular semisimple, there exists a finite subset
$(V,\theta )$
is generically regular semisimple, there exists a finite subset
![]() $D'\subset X$
such that
$D'\subset X$
such that
![]() $(V',\theta ')_{|X\setminus D'}$
is regular semisimple and that
$(V',\theta ')_{|X\setminus D'}$
is regular semisimple and that
![]() $D\subset D'$
. We set
$D\subset D'$
. We set
![]() $\mathcal{V}'=\mathcal{V}(\ast D')$
. For each
$\mathcal{V}'=\mathcal{V}(\ast D')$
. For each
![]() $P\in D'\setminus D$
, we consider the filtered bundle
$P\in D'\setminus D$
, we consider the filtered bundle
![]() $\mathcal{P}_{\ast }(\mathcal{V}'_P)$
over
$\mathcal{P}_{\ast }(\mathcal{V}'_P)$
over
![]() $\mathcal{V}'_P$
defined by
$\mathcal{V}'_P$
defined by
![]() $\mathcal{P}_a\mathcal{V}'_P =\mathcal{V}_P([a]P)$
, where
$\mathcal{P}_a\mathcal{V}'_P =\mathcal{V}_P([a]P)$
, where
![]() $[a]=\max \{n\in \mathbb{Z}\,|\,n\leqslant a\}$
. For harmonic metrics of
$[a]=\max \{n\in \mathbb{Z}\,|\,n\leqslant a\}$
. For harmonic metrics of
![]() $(V,t\theta )$
adapted to
$(V,t\theta )$
adapted to
![]() $\mathcal{P}_{\ast }\mathcal{V}$
, it is enough to study harmonic metrics of
$\mathcal{P}_{\ast }\mathcal{V}$
, it is enough to study harmonic metrics of
![]() $(V',t\theta ')$
adapted to
$(V',t\theta ')$
adapted to
![]() $\mathcal{P}_{\ast }\mathcal{V}'$
.
$\mathcal{P}_{\ast }\mathcal{V}'$
.
For any
![]() $P\in D$
, there exist a neighbourhood
$P\in D$
, there exist a neighbourhood
![]() $X_P$
of
$X_P$
of
![]() $P$
in
$P$
in
![]() $X$
and a decomposition of the meromorphic Higgs bundle
$X$
and a decomposition of the meromorphic Higgs bundle
such that the spectral curves of
![]() $(\mathcal{V}_{P,i},\theta _{P,i})_{|X_P\setminus \{P\}}$
are connected.
$(\mathcal{V}_{P,i},\theta _{P,i})_{|X_P\setminus \{P\}}$
are connected.
Condition 7.3. We assume the following conditions:
-
– the spectral curve
 $\Sigma _{V,\theta }$
is connected;
$\Sigma _{V,\theta }$
is connected;
-
– for any
 $P\in D$
, the decomposition (
48
) is compatible with the filtered bundle
$P\in D$
, the decomposition (
48
) is compatible with the filtered bundle
 $\mathcal{P}_{\ast }(\mathcal{V}_P)$
over
$\mathcal{P}_{\ast }(\mathcal{V}_P)$
over
 $\mathcal{V}_P$
, i.e.
$\mathcal{V}_P$
, i.e.
 $\mathcal{P}_{\ast }(\mathcal{V}_P) =\bigoplus _{i\in S(P)}\mathcal{P}_{\ast }\bigl ( (\mathcal{V}_{P,i})_P\bigr )$
.
$\mathcal{P}_{\ast }(\mathcal{V}_P) =\bigoplus _{i\in S(P)}\mathcal{P}_{\ast }\bigl ( (\mathcal{V}_{P,i})_P\bigr )$
.
For each
![]() $P\in D$
, we obtain the filtered bundle
$P\in D$
, we obtain the filtered bundle
![]() $\mathcal{P}^{\star }_{\ast }(\mathcal{V}_{P}) =\bigoplus _{i\in S(P)} \mathcal{P}^{\star }_{\ast }\bigl ( (\mathcal{V}_{P,i})_P\bigr )$
over
$\mathcal{P}^{\star }_{\ast }(\mathcal{V}_{P}) =\bigoplus _{i\in S(P)} \mathcal{P}^{\star }_{\ast }\bigl ( (\mathcal{V}_{P,i})_P\bigr )$
over
![]() $\mathcal{V}_{P}$
determined by the filtered bundles
$\mathcal{V}_{P}$
determined by the filtered bundles
![]() $\det (\mathcal{P}_{\ast }\mathcal{V}_{P,i})$
as in Proposition 5.13. By patching
$\det (\mathcal{P}_{\ast }\mathcal{V}_{P,i})$
as in Proposition 5.13. By patching
![]() $\mathcal{P}^{\star }_{\ast }(\mathcal{V}_{P})$
$\mathcal{P}^{\star }_{\ast }(\mathcal{V}_{P})$
![]() $(P\in D)$
with
$(P\in D)$
with
![]() $\mathcal{V}$
, we obtain a decomposable filtered Higgs bundle
$\mathcal{V}$
, we obtain a decomposable filtered Higgs bundle
![]() $(\mathcal{P}^{\star }_{\ast }(\mathcal{V}),\theta )$
.
$(\mathcal{P}^{\star }_{\ast }(\mathcal{V}),\theta )$
.
Lemma 7.4. The filtered Higgs bundle
![]() $(\mathcal{P}^{\star }_{\ast }(\mathcal{V}),\theta )$
is stable of degree
$(\mathcal{P}^{\star }_{\ast }(\mathcal{V}),\theta )$
is stable of degree
![]() $0$
. As a result, there exists a decoupled harmonic metric
$0$
. As a result, there exists a decoupled harmonic metric
![]() $h_{\infty }$
of
$h_{\infty }$
of
![]() $(V,\theta )$
adapted to
$(V,\theta )$
adapted to
![]() $\mathcal{P}^{\star }_{\ast }(\mathcal{V})$
.
$\mathcal{P}^{\star }_{\ast }(\mathcal{V})$
.
Proof.
Because
![]() $\Sigma _{V,\theta }$
is connected, there does not exist a non-trivial Higgs subbundle of
$\Sigma _{V,\theta }$
is connected, there does not exist a non-trivial Higgs subbundle of
![]() $(V,\theta )$
. Hence,
$(V,\theta )$
. Hence,
![]() $(\mathcal{P}_{\ast }\mathcal{V},\theta )$
is stable. Because
$(\mathcal{P}_{\ast }\mathcal{V},\theta )$
is stable. Because
![]() $\det (\mathcal{P}^{\star }_{\ast }\mathcal{V}) =\det (\mathcal{P}_{\ast }\mathcal{V})$
, we obtain
$\det (\mathcal{P}^{\star }_{\ast }\mathcal{V}) =\det (\mathcal{P}_{\ast }\mathcal{V})$
, we obtain
![]() $\deg (\mathcal{P}^{\star }_{\ast }\mathcal{V})=0$
. The second claim follows from Proposition 5.34.
$\deg (\mathcal{P}^{\star }_{\ast }\mathcal{V})=0$
. The second claim follows from Proposition 5.34.
Note that
![]() $\det (h_{\infty })$
is a flat metric of
$\det (h_{\infty })$
is a flat metric of
![]() $\det (V)$
adapted to
$\det (V)$
adapted to
![]() $\det (\mathcal{P}_{\ast }\mathcal{V})=\det (\mathcal{P}^{\star }_{\ast }\mathcal{V})$
. Because
$\det (\mathcal{P}_{\ast }\mathcal{V})=\det (\mathcal{P}^{\star }_{\ast }\mathcal{V})$
. Because
![]() $\Sigma _{V,\theta }$
is connected,
$\Sigma _{V,\theta }$
is connected,
![]() $(\mathcal{P}_{\ast }\mathcal{V},\theta )$
is stable of degree
$(\mathcal{P}_{\ast }\mathcal{V},\theta )$
is stable of degree
![]() $0$
as in Lemma 7.4. Hence, for any
$0$
as in Lemma 7.4. Hence, for any
![]() $t\gt 0$
, there exists a harmonic metric
$t\gt 0$
, there exists a harmonic metric
![]() $h_t$
of
$h_t$
of
![]() $(V,t\theta )$
which is adapted to
$(V,t\theta )$
which is adapted to
![]() $\mathcal{P}_{\ast }\mathcal{V}$
such that
$\mathcal{P}_{\ast }\mathcal{V}$
such that
![]() $\det (h_t)=\det (h_{\infty })$
.
$\det (h_t)=\det (h_{\infty })$
.
Theorem 7.5.
On any relatively compact open subset
![]() $K\subset X\setminus D$
, the sequence
$K\subset X\setminus D$
, the sequence
![]() $h_{t}$
is convergent to
$h_{t}$
is convergent to
![]() $h_{\infty }$
in the
$h_{\infty }$
in the
![]() $C^{\infty }$
-sense.
$C^{\infty }$
-sense.
7.1.2 The case of locally and globally irreducible Higgs bundles
We state Theorem7.5 in a special case for clarification (see also Remark 7.2). Let
![]() $(E,\overline{\partial }_E,\theta )$
be a generically regular semisimple Higgs bundle of degree
$(E,\overline{\partial }_E,\theta )$
be a generically regular semisimple Higgs bundle of degree
![]() $0$
on
$0$
on
![]() $X$
. Let
$X$
. Let
![]() $\Sigma _{E,\theta }$
denote the spectral curve. There exists the finite subset
$\Sigma _{E,\theta }$
denote the spectral curve. There exists the finite subset
![]() $D(E,\theta )\subset X$
such that the following holds:
$D(E,\theta )\subset X$
such that the following holds:
-
–
 $P\in D(E,\theta )$
if and only if
$P\in D(E,\theta )$
if and only if
 $|T_P^{\ast }X\cap \Sigma _{E,\theta }|\lt r$
.
$|T_P^{\ast }X\cap \Sigma _{E,\theta }|\lt r$
.
We impose the following condition.
Condition 7.6.
-
– The spectral curve
 $\Sigma _{E,\theta }$
is irreducible, i.e.
$\Sigma _{E,\theta }$
is irreducible, i.e.
 $\Sigma _{E,\theta }\setminus \pi ^{-1}(D(E,\theta ))$
is connected.
$\Sigma _{E,\theta }\setminus \pi ^{-1}(D(E,\theta ))$
is connected.
-
– For any
 $P\in D(E,\theta )$
, there exist a neighbourhood
$P\in D(E,\theta )$
, there exist a neighbourhood
 $X_P$
of
$X_P$
of
 $P$
in
$P$
in
 $X$
and a decomposition
(49)such that the spectral curves
$X$
and a decomposition
(49)such that the spectral curves \begin{align} (E,\theta )_{|X_P} =\bigoplus _{i\in S(P)} (E_{P,i},\theta _{P,i}), \end{align}
\begin{align} (E,\theta )_{|X_P} =\bigoplus _{i\in S(P)} (E_{P,i},\theta _{P,i}), \end{align}
 $\Sigma _{E_{P,i},\theta _{P,i}}$
are irreducible.
$\Sigma _{E_{P,i},\theta _{P,i}}$
are irreducible.
We set
![]() $D=D(E,\theta )$
. Let
$D=D(E,\theta )$
. Let
![]() $\mathcal{P}^{(0)}_{\ast }(E(\ast D)_P)$
be the filtered bundle over
$\mathcal{P}^{(0)}_{\ast }(E(\ast D)_P)$
be the filtered bundle over
![]() $E(\ast D)_P$
defined by
$E(\ast D)_P$
defined by
![]() $\mathcal{P}^{(0)}_a(E(\ast D)_P)=E_P([a]P)$
, where
$\mathcal{P}^{(0)}_a(E(\ast D)_P)=E_P([a]P)$
, where
![]() $[a]=\max \{n\in \mathbb{Z}\,|\,n\leqslant a\}$
. Because there exists the decomposition
$[a]=\max \{n\in \mathbb{Z}\,|\,n\leqslant a\}$
. Because there exists the decomposition
induced by (49), we obtain the filtered bundle
![]() $\mathcal{P}^{\star }_{\ast }(E(\ast D)_P)$
determined by
$\mathcal{P}^{\star }_{\ast }(E(\ast D)_P)$
determined by
![]() $\det (\mathcal{P}^{(0)}_{\ast }E_{P,i}(\ast D)_P)$
as in Proposition 5.13. By patching them with
$\det (\mathcal{P}^{(0)}_{\ast }E_{P,i}(\ast D)_P)$
as in Proposition 5.13. By patching them with
![]() $(E(\ast D),\theta )$
, we obtain a filtered bundle
$(E(\ast D),\theta )$
, we obtain a filtered bundle
![]() $\mathcal{P}^{\star }_{\ast }\mathcal{V}$
over
$\mathcal{P}^{\star }_{\ast }\mathcal{V}$
over
![]() $\mathcal{V}=E(\ast D)$
. The filtered Higgs bundle
$\mathcal{V}=E(\ast D)$
. The filtered Higgs bundle
![]() $(\mathcal{P}^{\star }_{\ast }(E(\ast D)),\theta )$
is decomposable.
$(\mathcal{P}^{\star }_{\ast }(E(\ast D)),\theta )$
is decomposable.
As in Lemma 7.4, there exists a decoupled harmonic metric
![]() $h_{\infty }$
of
$h_{\infty }$
of
![]() $(E,\theta )_{|X\setminus D}$
such that
$(E,\theta )_{|X\setminus D}$
such that
![]() $h_{\infty }$
is adapted to
$h_{\infty }$
is adapted to
![]() $\mathcal{P}^{\star }_{\ast }\mathcal{V}$
. For any
$\mathcal{P}^{\star }_{\ast }\mathcal{V}$
. For any
![]() $t\gt 0$
, there exists a unique harmonic metric
$t\gt 0$
, there exists a unique harmonic metric
![]() $h_t$
of
$h_t$
of
![]() $(E,t\theta )$
such that
$(E,t\theta )$
such that
![]() $\det (h_t)=\det (h_{\infty })$
. As a special case of Theorem7.5, we obtain the following.
$\det (h_t)=\det (h_{\infty })$
. As a special case of Theorem7.5, we obtain the following.
Corollary 7.7.
On any relatively compact open subset
![]() $K\subset X\setminus D$
, the sequence
$K\subset X\setminus D$
, the sequence
![]() $h_{t}$
is convergent to
$h_{t}$
is convergent to
![]() $h_{\infty }$
in the
$h_{\infty }$
in the
![]() $C^{\infty }$
-sense.
$C^{\infty }$
-sense.
Remark 7.8. The second condition in Condition 7.6 is satisfied if
![]() $\Sigma _{E,\theta }$
is locally irreducible.
$\Sigma _{E,\theta }$
is locally irreducible.
7.1.3 Proof of Theorem7.5
Let
![]() $P\in D$
. We set
$P\in D$
. We set
![]() $X_P^{\ast }=X_P\setminus \{P\}$
. We set
$X_P^{\ast }=X_P\setminus \{P\}$
. We set
![]() $V_{P,i}=\mathcal{V}_{P,i|X_P^{\ast }}$
and
$V_{P,i}=\mathcal{V}_{P,i|X_P^{\ast }}$
and
![]() $r(P,i)=\mathop{\textrm{rank}}\nolimits V_{P,i}$
. Let
$r(P,i)=\mathop{\textrm{rank}}\nolimits V_{P,i}$
. Let
![]() $z_P$
be a holomorphic coordinate of
$z_P$
be a holomorphic coordinate of
![]() $X_P$
by which
$X_P$
by which
![]() $X_P\simeq \bigl \{z\in \mathbb{C}\,\big |\,|z|\lt 2\bigr \}$
. We set
$X_P\simeq \bigl \{z\in \mathbb{C}\,\big |\,|z|\lt 2\bigr \}$
. We set
![]() $(h_{\infty })_{P,i}:=h_{\infty |V_{P,i}}$
. Let
$(h_{\infty })_{P,i}:=h_{\infty |V_{P,i}}$
. Let
![]() $h_{t,P,i}$
be a harmonic metric of
$h_{t,P,i}$
be a harmonic metric of
![]() $(V_{P,i},t\theta _{P,i})$
such that (i) the boundary value at
$(V_{P,i},t\theta _{P,i})$
such that (i) the boundary value at
![]() $|z_P|=1$
is equal to that of
$|z_P|=1$
is equal to that of
![]() $(h_{\infty })_{P,i}$
and (ii)
$(h_{\infty })_{P,i}$
and (ii)
![]() $h_{t,P,i}$
is adapted to
$h_{t,P,i}$
is adapted to
![]() $\mathcal{P}_{\ast }\mathcal{V}_{P,i}$
. We have
$\mathcal{P}_{\ast }\mathcal{V}_{P,i}$
. We have
![]() $\det (h_{t,P,i})=\det ((h_{\infty })_{P,i})$
. We obtain the following lemma by Proposition 6.6.
$\det (h_{t,P,i})=\det ((h_{\infty })_{P,i})$
. We obtain the following lemma by Proposition 6.6.
Lemma 7.9.
The sequence
![]() $h_{t,P,i}$
is convergent to
$h_{t,P,i}$
is convergent to
![]() $(h_{\infty })_{P,i}$
as
$(h_{\infty })_{P,i}$
as
![]() $t\to \infty$
in the
$t\to \infty$
in the
![]() $C^{\infty }$
-sense on any relatively compact open subset of
$C^{\infty }$
-sense on any relatively compact open subset of
![]() $X_P^{\ast }$
.
$X_P^{\ast }$
.
We regard
![]() $X_P$
as an open subset of
$X_P$
as an open subset of
![]() $\mathbb{C}$
by the coordinate
$\mathbb{C}$
by the coordinate
![]() $z_P$
. Let
$z_P$
. Let
![]() $\varphi _{P,r(P,i)}:\mathbb{C}\to \mathbb{C}$
be defined by
$\varphi _{P,r(P,i)}:\mathbb{C}\to \mathbb{C}$
be defined by
![]() $\varphi _{P,r(P,i)}(\zeta _{P,i})=\zeta _{P,i}^{r(P,i)}$
. We set
$\varphi _{P,r(P,i)}(\zeta _{P,i})=\zeta _{P,i}^{r(P,i)}$
. We set
![]() $X_P^{(r(P,i))}=\varphi _{P,r(P,i)}^{-1}(X_P)$
and
$X_P^{(r(P,i))}=\varphi _{P,r(P,i)}^{-1}(X_P)$
and
![]() $X_P^{(r(P,i))\ast }=\varphi _{P,r(P,i)}^{-1}(X_P^{\ast })$
. The induced maps
$X_P^{(r(P,i))\ast }=\varphi _{P,r(P,i)}^{-1}(X_P^{\ast })$
. The induced maps
![]() $X_P^{(r(P,i))}\to X_P$
and
$X_P^{(r(P,i))}\to X_P$
and
![]() $X_P^{(r(P,i))\ast }\to X_P^{\ast }$
are also denoted by
$X_P^{(r(P,i))\ast }\to X_P^{\ast }$
are also denoted by
![]() $\varphi _{P,r(P,i)}$
.
$\varphi _{P,r(P,i)}$
.
We define a Hermitian product
![]() $h_{t,P,i}^{(r(P,i))}$
of
$h_{t,P,i}^{(r(P,i))}$
of
![]() $\varphi _{P,r(P,i)}^{\ast }(V_{P,i})_{|X_P^{(r(P,i))\ast }}$
as follows. We have the decomposition
$\varphi _{P,r(P,i)}^{\ast }(V_{P,i})_{|X_P^{(r(P,i))\ast }}$
as follows. We have the decomposition
 \begin{align*} \varphi _{P,r(P,i)}^{\ast } (V_{P,i},\theta _{P,i})_{|X_P^{(r(P,i))\ast }} =\bigoplus _{p=1}^{r(P,i)} (V_{P,i,\beta (p)},\beta (p)\,d\zeta _{P,i}), \end{align*}
\begin{align*} \varphi _{P,r(P,i)}^{\ast } (V_{P,i},\theta _{P,i})_{|X_P^{(r(P,i))\ast }} =\bigoplus _{p=1}^{r(P,i)} (V_{P,i,\beta (p)},\beta (p)\,d\zeta _{P,i}), \end{align*}
where
![]() $\beta (p)$
are meromorphic functions on
$\beta (p)$
are meromorphic functions on
![]() $X_P^{(r(P,i))}$
. Let
$X_P^{(r(P,i))}$
. Let
![]() $v_{\beta (1)}$
be a holomorphic frame of
$v_{\beta (1)}$
be a holomorphic frame of
![]() $V_{P,i,\beta (1)}$
. We obtain a frame
$V_{P,i,\beta (1)}$
. We obtain a frame
![]() $v_{\sigma ^{\ast }\beta (1)}=\sigma ^{\ast }(v_{\beta (1)})$
of
$v_{\sigma ^{\ast }\beta (1)}=\sigma ^{\ast }(v_{\beta (1)})$
of
![]() $V_{P,i,\sigma ^{\ast }\beta (1)}$
. Let
$V_{P,i,\sigma ^{\ast }\beta (1)}$
. Let
![]() $\chi (\zeta _{P,i})$
be an
$\chi (\zeta _{P,i})$
be an
![]() $\mathbb{R}_{\geqslant 0}$
-valued function such that (i)
$\mathbb{R}_{\geqslant 0}$
-valued function such that (i)
![]() $\chi (\zeta _{P,i})$
depends only on
$\chi (\zeta _{P,i})$
depends only on
![]() $|\zeta _{P,i}|$
and (ii)
$|\zeta _{P,i}|$
and (ii)
![]() $\chi (\zeta _{P,i})=1$
$\chi (\zeta _{P,i})=1$
![]() $(|\zeta _{P,i}|\leqslant 1/2)$
,
$(|\zeta _{P,i}|\leqslant 1/2)$
,
![]() $\chi (\zeta _{P,i})=0$
$\chi (\zeta _{P,i})=0$
![]() $(|\zeta _{P,i}|\geqslant 2/3)$
. For
$(|\zeta _{P,i}|\geqslant 2/3)$
. For
![]() $p\neq q$
, we put
$p\neq q$
, we put
We define
![]() $h_{t,P,i}^{(r(P,i))}(v_{\beta (p)},v_{\beta (p)})$
by
$h_{t,P,i}^{(r(P,i))}(v_{\beta (p)},v_{\beta (p)})$
by
 \begin{align} \log h_{t,P,i}^{(r(P,i))}(v_{\beta (p)},v_{\beta (p)}) &= \chi (\zeta _{P,i}) \log \varphi _{P,r(P)}^{\ast }(h_{t,P,i})(v_{\beta (p)},v_{\beta (p)})\nonumber\\& \quad\qquad+(1-\chi (\zeta (P,i))) \log \varphi _{P,r(P)}^{\ast }\bigl ( (h_{\infty })_{P,i}^{(r(P,i))} \bigr )(v_{\beta (p)},v_{\beta (p)}). \end{align}
\begin{align} \log h_{t,P,i}^{(r(P,i))}(v_{\beta (p)},v_{\beta (p)}) &= \chi (\zeta _{P,i}) \log \varphi _{P,r(P)}^{\ast }(h_{t,P,i})(v_{\beta (p)},v_{\beta (p)})\nonumber\\& \quad\qquad+(1-\chi (\zeta (P,i))) \log \varphi _{P,r(P)}^{\ast }\bigl ( (h_{\infty })_{P,i}^{(r(P,i))} \bigr )(v_{\beta (p)},v_{\beta (p)}). \end{align}
Then,
![]() $h^{(r(P,i))}_{t,P,i}$
is
$h^{(r(P,i))}_{t,P,i}$
is
![]() $\mathop{\textrm{Gal}}\nolimits (r(P,i))$
-invariant, and we have
$\mathop{\textrm{Gal}}\nolimits (r(P,i))$
-invariant, and we have
![]() $h^{(r(P,i))}_{t,P,i}=\varphi _{P,r(P,i)}^{-1}(h_{t,P,i})$
on
$h^{(r(P,i))}_{t,P,i}=\varphi _{P,r(P,i)}^{-1}(h_{t,P,i})$
on
![]() $\{0\lt |\zeta _{P,i}|\lt 1/4\}$
and
$\{0\lt |\zeta _{P,i}|\lt 1/4\}$
and
![]() $h^{(r(P,i))}_{t,P,i} =\varphi _{P,r(P,i)}^{-1}\bigl ((h_{\infty })_{P,i}\bigr )$
on
$h^{(r(P,i))}_{t,P,i} =\varphi _{P,r(P,i)}^{-1}\bigl ((h_{\infty })_{P,i}\bigr )$
on
![]() $\{4/5\lt |\zeta _{P,i}|\}$
. There exists a Hermitian metric
$\{4/5\lt |\zeta _{P,i}|\}$
. There exists a Hermitian metric
![]() $\widetilde{h}_{t,P,i}$
of
$\widetilde{h}_{t,P,i}$
of
![]() $V_{P,i}$
such that
$V_{P,i}$
such that
![]() $\varphi _{P,r(P,i)}^{-1}(\widetilde{h}_{t,P,i}) =h^{(r(P,i))}_{t,P,i}$
on
$\varphi _{P,r(P,i)}^{-1}(\widetilde{h}_{t,P,i}) =h^{(r(P,i))}_{t,P,i}$
on
![]() $X_P^{(r(P,i))\ast }$
. We obtain a Hermitian metric
$X_P^{(r(P,i))\ast }$
. We obtain a Hermitian metric
of
![]() $V_{|X_P^{\ast }}$
. By patching
$V_{|X_P^{\ast }}$
. By patching
![]() $\widetilde{h}_{t,P}$
and
$\widetilde{h}_{t,P}$
and
![]() $h_{\infty }$
, we obtain Hermitian metrics
$h_{\infty }$
, we obtain Hermitian metrics
![]() $\widetilde{h}'_{t}$
of
$\widetilde{h}'_{t}$
of
![]() $V$
. We obtain the
$V$
. We obtain the
![]() $C^{\infty }$
-function
$C^{\infty }$
-function
![]() $\alpha _t$
on
$\alpha _t$
on
![]() $X\setminus D$
determined by
$X\setminus D$
determined by
![]() $\det (\widetilde{h}'_t)=e^{\alpha _t}\det (h_{\infty })$
. We set
$\det (\widetilde{h}'_t)=e^{\alpha _t}\det (h_{\infty })$
. We set
![]() $\widetilde{h}_t=e^{-\alpha _t/r}\widetilde{h}'_t$
. By the construction, the following lemma is clear.
$\widetilde{h}_t=e^{-\alpha _t/r}\widetilde{h}'_t$
. By the construction, the following lemma is clear.
Lemma 7.10.
There exists
![]() $t_0$
such that
$t_0$
such that
![]() $\widetilde{h}_{t}$
is positive definite for any
$\widetilde{h}_{t}$
is positive definite for any
![]() $t\geqslant t_0$
. Moreover, the following holds.
$t\geqslant t_0$
. Moreover, the following holds.
-
– The sequence
 $\widetilde{h}_t$
is convergent to
$\widetilde{h}_t$
is convergent to
 $h_{\infty }$
in the
$h_{\infty }$
in the
 $C^{\infty }$
-sense on any relatively compact open subset of
$C^{\infty }$
-sense on any relatively compact open subset of
 $X\setminus D$
. The support of
$X\setminus D$
. The support of
 $R(\widetilde{h}_{t})+ [t\theta, (t\theta )^{\dagger }_{\widetilde{h}_{t}}]$
is contained in
$R(\widetilde{h}_{t})+ [t\theta, (t\theta )^{\dagger }_{\widetilde{h}_{t}}]$
is contained in
 $\{\left ({1 \over 4}\right )^{\mathop{\textrm{rank}}\nolimits (E)} \leqslant |z_P|\leqslant {4 \over 5}\}$
for
$\{\left ({1 \over 4}\right )^{\mathop{\textrm{rank}}\nolimits (E)} \leqslant |z_P|\leqslant {4 \over 5}\}$
for
 $P\in D$
. In particular,
(51)as
$P\in D$
. In particular,
(51)as \begin{align} \int _X \Bigl | R(\widetilde{h}_{t})+[t\theta, (t\theta )^{\dagger }_{\widetilde{h}_{t}}] \Bigr |_{\widetilde{h}_{t},g_X} \to 0, \end{align}
\begin{align} \int _X \Bigl | R(\widetilde{h}_{t})+[t\theta, (t\theta )^{\dagger }_{\widetilde{h}_{t}}] \Bigr |_{\widetilde{h}_{t},g_X} \to 0, \end{align}
 $t\to \infty$
.
$t\to \infty$
.
Let
![]() $g_X$
be a Kähler metric of
$g_X$
be a Kähler metric of
![]() $X$
. Let
$X$
. Let
![]() $s_{t}$
denote the automorphism of
$s_{t}$
denote the automorphism of
![]() $V$
determined by
$V$
determined by
![]() $h_t=\widetilde{h}_{t}s_{t}$
. We have
$h_t=\widetilde{h}_{t}s_{t}$
. We have
![]() $\det (s_{t})=1$
. According to [Reference SimpsonSim88, Lemma 3.1], we obtain the following on
$\det (s_{t})=1$
. According to [Reference SimpsonSim88, Lemma 3.1], we obtain the following on
![]() $X\setminus D$
:
$X\setminus D$
:
Note that
![]() $\bigoplus _{i\in S(P)} h_{t,P,i}$
and
$\bigoplus _{i\in S(P)} h_{t,P,i}$
and
![]() $h_{t|X_P^{\ast }}$
are mutually bounded for any
$h_{t|X_P^{\ast }}$
are mutually bounded for any
![]() $P\in D$
. Hence,
$P\in D$
. Hence,
![]() ${\mathop{\textrm{Tr}}\nolimits }(s_t)$
is bounded. We also note the following vanishing (see Lemma [Reference MochizukiMoc21, Lemma 4.7]):
${\mathop{\textrm{Tr}}\nolimits }(s_t)$
is bounded. We also note the following vanishing (see Lemma [Reference MochizukiMoc21, Lemma 4.7]):
We set
![]() $b_{t}=\sup _{X\setminus D}{\mathop{\textrm{Tr}}\nolimits }(s_{t})$
. Note that
$b_{t}=\sup _{X\setminus D}{\mathop{\textrm{Tr}}\nolimits }(s_{t})$
. Note that
![]() $b_{t}\geqslant \mathop{\textrm{rank}}\nolimits (E)$
, and
$b_{t}\geqslant \mathop{\textrm{rank}}\nolimits (E)$
, and
![]() $b_t=\mathop{\textrm{rank}}\nolimits (E)$
if and only if
$b_t=\mathop{\textrm{rank}}\nolimits (E)$
if and only if
![]() $s_t={\mathop{\textrm{id}}\nolimits }_E$
. We set
$s_t={\mathop{\textrm{id}}\nolimits }_E$
. We set
![]() $u_{t}=b_{t}^{-1}\cdot s_{t}$
. There exists
$u_{t}=b_{t}^{-1}\cdot s_{t}$
. There exists
![]() $C\gt 0$
, which is independent of
$C\gt 0$
, which is independent of
![]() $t$
such that
$t$
such that
![]() $|u_{t}|_{\widetilde{h}_{t}}\leqslant C$
. By (51), (52) and (53) we obtain
$|u_{t}|_{\widetilde{h}_{t}}\leqslant C$
. By (51), (52) and (53) we obtain
as
![]() $t\to \infty$
.
$t\to \infty$
.
Let
![]() $t(i)\gt 0$
be a sequence such that
$t(i)\gt 0$
be a sequence such that
![]() $t(i)\to \infty$
as
$t(i)\to \infty$
as
![]() $i\to \infty$
. By going to a subsequence,
$i\to \infty$
. By going to a subsequence,
![]() $u_{t(i)}$
is weakly convergent in
$u_{t(i)}$
is weakly convergent in
![]() $L_1^2$
locally on
$L_1^2$
locally on
![]() $X\setminus D$
. In particular, it is convergent in
$X\setminus D$
. In particular, it is convergent in
![]() $L^q$
for any
$L^q$
for any
![]() $q\geqslant 1$
locally on
$q\geqslant 1$
locally on
![]() $X\setminus D$
. Let
$X\setminus D$
. Let
![]() $u_{\infty }$
denote the limit which satisfies
$u_{\infty }$
denote the limit which satisfies
![]() $\overline{\partial } u_{\infty }=[\theta, u_{\infty }]=0$
.
$\overline{\partial } u_{\infty }=[\theta, u_{\infty }]=0$
.
Lemma 7.11. We have
![]() $u_{\infty }\neq 0$
.
$u_{\infty }\neq 0$
.
Proof.
Note that
![]() $\sup _X{\mathop{\textrm{Tr}}\nolimits }(u_{t(i)})=1$
for any
$\sup _X{\mathop{\textrm{Tr}}\nolimits }(u_{t(i)})=1$
for any
![]() $i$
. Let
$i$
. Let
![]() $0\lt \epsilon \lt 1$
. Let
$0\lt \epsilon \lt 1$
. Let
![]() $P_{i}\in X$
be points such that
$P_{i}\in X$
be points such that
![]() ${\mathop{\textrm{Tr}}\nolimits }(u_{t})(P_{i})\geqslant \epsilon$
. By going to a subsequence, we may assume that the sequence is convergent to a point
${\mathop{\textrm{Tr}}\nolimits }(u_{t})(P_{i})\geqslant \epsilon$
. By going to a subsequence, we may assume that the sequence is convergent to a point
![]() $P_{\infty }$
. Let us consider the case where
$P_{\infty }$
. Let us consider the case where
Let
![]() $(X_{P_{\infty }},z)$
be a holomorphic coordinate neighbourhood around
$(X_{P_{\infty }},z)$
be a holomorphic coordinate neighbourhood around
![]() $P_{\infty }$
, which does not intersect with
$P_{\infty }$
, which does not intersect with
![]() $W$
. Because
$W$
. Because
![]() $F(\widetilde{h}_{t})=0$
on
$F(\widetilde{h}_{t})=0$
on
![]() $X_{P_{\infty }}$
, we obtain
$X_{P_{\infty }}$
, we obtain
![]() $\Delta _{g_X}{\mathop{\textrm{Tr}}\nolimits }(u_{t})\leqslant 0$
. By the mean value property of the subharmonic functions, there exists
$\Delta _{g_X}{\mathop{\textrm{Tr}}\nolimits }(u_{t})\leqslant 0$
. By the mean value property of the subharmonic functions, there exists
![]() $C\gt 0$
such that
$C\gt 0$
such that
Because
![]() $u_{t(i)}$
is convergent to
$u_{t(i)}$
is convergent to
![]() $u_{\infty }$
in
$u_{\infty }$
in
![]() $L^p$
for any
$L^p$
for any
![]() $p\geqslant 1$
on
$p\geqslant 1$
on
![]() $X_{P_{\infty }}$
, we obtain that
$X_{P_{\infty }}$
, we obtain that
![]() $u_{\infty }\neq 0$
.
$u_{\infty }\neq 0$
.
Let us consider the case where
![]() $P_{\infty }\in \{|z_P|\lt 4/5\}$
for some
$P_{\infty }\in \{|z_P|\lt 4/5\}$
for some
![]() $P\in D$
. Let
$P\in D$
. Let
![]() $(X_P,z_P)$
be a holomorphic coordinate neighbourhood around
$(X_P,z_P)$
be a holomorphic coordinate neighbourhood around
![]() $P$
as above. By [Reference SimpsonSim88, Lemma 3.1], we have
$P$
as above. By [Reference SimpsonSim88, Lemma 3.1], we have
There exist
![]() $C^{\infty }$
-functions
$C^{\infty }$
-functions
![]() $\alpha _{i}$
on
$\alpha _{i}$
on
![]() $X_{P}$
such that (i)
$X_{P}$
such that (i)
![]() $\Delta _{g_X} \alpha _{i} =\Bigl |R(\widetilde{h}_{t(i)})+[t\theta, (t\theta )^{\dagger }_{\widetilde{h}_{t(i)}}] \Bigr |_{\widetilde{h}_{t(i)},g_X}$
, (ii)
$\Delta _{g_X} \alpha _{i} =\Bigl |R(\widetilde{h}_{t(i)})+[t\theta, (t\theta )^{\dagger }_{\widetilde{h}_{t(i)}}] \Bigr |_{\widetilde{h}_{t(i)},g_X}$
, (ii)
![]() $\alpha _{i|{\partial } X_{P}}=0$
and (iii) there exists
$\alpha _{i|{\partial } X_{P}}=0$
and (iii) there exists
![]() $C\gt 0$
such that
$C\gt 0$
such that
![]() $|\alpha _{i}|\leqslant C$
for any
$|\alpha _{i}|\leqslant C$
for any
![]() $i$
. Because
$i$
. Because
![]() $\log{\mathop{\textrm{Tr}}\nolimits }(u_{t(i)})-\alpha _i$
is a subharmonic function on
$\log{\mathop{\textrm{Tr}}\nolimits }(u_{t(i)})-\alpha _i$
is a subharmonic function on
![]() $X_P$
, the maximum principle allows us to obtain
$X_P$
, the maximum principle allows us to obtain
Hence, there exists a sequence
![]() $P'_i\in{\partial } X_{P}$
such that
$P'_i\in{\partial } X_{P}$
such that
![]() ${\mathop{\textrm{Tr}}\nolimits }(u_{t(i)})(P'_i)\geqslant \epsilon e^{-C}$
. By going to a subsequence, we may assume that the sequence
${\mathop{\textrm{Tr}}\nolimits }(u_{t(i)})(P'_i)\geqslant \epsilon e^{-C}$
. By going to a subsequence, we may assume that the sequence
![]() $P'_i$
is convergent to
$P'_i$
is convergent to
![]() $P'_{\infty }\in X\setminus W$
. Then, we can apply the result in the first part of this proof.
$P'_{\infty }\in X\setminus W$
. Then, we can apply the result in the first part of this proof.
Recall that
![]() $u_{\infty }\neq 0$
is an endomorphism of
$u_{\infty }\neq 0$
is an endomorphism of
![]() $(V,\theta )$
such that
$(V,\theta )$
such that
![]() $\overline{\partial } u_{\infty }=[\theta, u_{\infty }]=0$
. At each point of
$\overline{\partial } u_{\infty }=[\theta, u_{\infty }]=0$
. At each point of
![]() $X\setminus D$
, an eigenspace of
$X\setminus D$
, an eigenspace of
![]() $\theta$
is also an eigenspace of
$\theta$
is also an eigenspace of
![]() $u_{\infty }$
. Because each
$u_{\infty }$
. Because each
![]() $u_{t(i)}$
is self-adjoint with respect to
$u_{t(i)}$
is self-adjoint with respect to
![]() $\widetilde{h}_{t}$
,
$\widetilde{h}_{t}$
,
![]() $u_{\infty }$
is self-adjoint with respect to
$u_{\infty }$
is self-adjoint with respect to
![]() $h_{\infty }$
. We obtain
$h_{\infty }$
. We obtain
![]() ${\partial }_{h_{\infty }}u_{\infty }=0$
. Hence, the eigenvalues of
${\partial }_{h_{\infty }}u_{\infty }=0$
. Hence, the eigenvalues of
![]() $u_{\infty }$
are constant. Because
$u_{\infty }$
are constant. Because
![]() $\widetilde{h}_t(u_{t(i)}v,v)\geqslant 0$
for any local section
$\widetilde{h}_t(u_{t(i)}v,v)\geqslant 0$
for any local section
![]() $v$
of
$v$
of
![]() $V$
, we obtain
$V$
, we obtain
![]() $h_{\infty }(u_{\infty }v,v)\geqslant 0$
, which implies that the eigenvalues of
$h_{\infty }(u_{\infty }v,v)\geqslant 0$
, which implies that the eigenvalues of
![]() $u_{\infty }$
are non-negative. We also note that
$u_{\infty }$
are non-negative. We also note that
![]() $\Sigma _{V,\theta }$
is connected. Hence,
$\Sigma _{V,\theta }$
is connected. Hence,
![]() $u_{\infty }$
is a positive constant multiplication. This implies that the sequence
$u_{\infty }$
is a positive constant multiplication. This implies that the sequence
![]() $b_{t}$
is bounded, and that the subsequence
$b_{t}$
is bounded, and that the subsequence
![]() $s_{t(i)}$
is convergent to a positive constant multiplication. Because
$s_{t(i)}$
is convergent to a positive constant multiplication. Because
![]() $\det (s_{t})=1$
, the limit is the identity. Because this is independent of the choice of a subsequence, we obtain the desired convergence.
$\det (s_{t})=1$
, the limit is the identity. Because this is independent of the choice of a subsequence, we obtain the desired convergence.
7.2 Order of convergence in a smooth case
7.2.1 Rough statement
Let us study the order of the convergence in the situation of §7.1.2 assuming the following stronger condition.
Condition 7.12.
Let
![]() $\rho :\widetilde{\Sigma }_{E,\theta }\to \Sigma _{E,\theta }$
be the normalization. There exists a line bundle
$\rho :\widetilde{\Sigma }_{E,\theta }\to \Sigma _{E,\theta }$
be the normalization. There exists a line bundle
![]() $L$
on
$L$
on
![]() $\widetilde{\Sigma }_{E,\theta }$
with an isomorphism
$\widetilde{\Sigma }_{E,\theta }$
with an isomorphism
![]() $(\pi \circ \rho )_{\ast }L\simeq E$
such that
$(\pi \circ \rho )_{\ast }L\simeq E$
such that
![]() $\theta$
is induced by the
$\theta$
is induced by the
![]() $\mathcal{O}_{T^{\ast }X}$
-action on
$\mathcal{O}_{T^{\ast }X}$
-action on
![]() $\rho _{\ast }L$
.
$\rho _{\ast }L$
.
Let
![]() $g(\widetilde{\Sigma }_{E,\theta })$
and
$g(\widetilde{\Sigma }_{E,\theta })$
and
![]() $g(X)$
denote the genus of
$g(X)$
denote the genus of
![]() $\widetilde{\Sigma }_{E,\theta }$
and
$\widetilde{\Sigma }_{E,\theta }$
and
![]() $X$
, respectively. Then, we have
$X$
, respectively. Then, we have
![]() $\deg (L)=g(\widetilde{\Sigma }_{E,\theta })-rg(X)+r-1$
.
$\deg (L)=g(\widetilde{\Sigma }_{E,\theta })-rg(X)+r-1$
.
Remark 7.13. If Condition 7.12 is satisfied, Condition 7.6 is also satisfied. Condition 7.12 is satisfied if
![]() $\Sigma _{E,\theta }$
is smooth and connected.
$\Sigma _{E,\theta }$
is smooth and connected.
We set
![]() $(V,\theta )=(E,\theta )_{|X\setminus D}$
. Let
$(V,\theta )=(E,\theta )_{|X\setminus D}$
. Let
![]() $s(h_{\infty },h_t)$
be the automorphism of
$s(h_{\infty },h_t)$
be the automorphism of
![]() $V$
determined by
$V$
determined by
![]() $h_t=h_{\infty }\cdot s(h_{\infty },h_t)$
. Let
$h_t=h_{\infty }\cdot s(h_{\infty },h_t)$
. Let
![]() $g_X$
be a Kähler metric of
$g_X$
be a Kähler metric of
![]() $X$
.
$X$
.
Theorem 7.14.
For any relatively compact open subset
![]() $K$
of
$K$
of
![]() $X\setminus D$
and a non-negative integer
$X\setminus D$
and a non-negative integer
![]() $\ell$
, there exist positive constants
$\ell$
, there exist positive constants
![]() $C(K,\ell )$
and
$C(K,\ell )$
and
![]() $\epsilon (K,\ell )$
such that the
$\epsilon (K,\ell )$
such that the
![]() $L_{\ell }^2$
-norms of
$L_{\ell }^2$
-norms of
![]() $s(h_{\infty },h_t)-{\mathop{\textrm{id}}\nolimits }_E$
on
$s(h_{\infty },h_t)-{\mathop{\textrm{id}}\nolimits }_E$
on
![]() $K$
with respect to
$K$
with respect to
![]() $h_{\infty }$
,
$h_{\infty }$
,
![]() $g_X$
and the Chern connection of
$g_X$
and the Chern connection of
![]() $h_{\infty }$
are dominated by
$h_{\infty }$
are dominated by
![]() $C(K,\ell )e^{-\epsilon (K,\ell )t}$
.
$C(K,\ell )e^{-\epsilon (K,\ell )t}$
.
7.2.2 Refined statement
We shall prove a refined statement. For that purpose, we refine the construction of
![]() $\widetilde{h}_t$
in the proof of Theorem7.5. Let
$\widetilde{h}_t$
in the proof of Theorem7.5. Let
![]() $P\in D$
and
$P\in D$
and
![]() $i\in S(P)$
.
$i\in S(P)$
.
Lemma 7.15. The metric
![]() $\det ((h_{\infty })_{P,i})$
induces a flat metric of
$\det ((h_{\infty })_{P,i})$
induces a flat metric of
![]() $\det (E_{P,i})$
.
$\det (E_{P,i})$
.
Proof.
The lemma follows from the condition that
![]() $\det ((h_{\infty })_{P,i})$
is adapted to
$\det ((h_{\infty })_{P,i})$
is adapted to
![]() $\det \mathcal{P}^{\star }_{\ast }(E_{P,i}(\ast D)_P) =\det \mathcal{P}^{(0)}_{\ast }(E_{P,i}(\ast D)_P)$
.
$\det \mathcal{P}^{\star }_{\ast }(E_{P,i}(\ast D)_P) =\det \mathcal{P}^{(0)}_{\ast }(E_{P,i}(\ast D)_P)$
.
According to Proposition 6.11, there exists a non-degenerate symmetric pairing
![]() $C_{P,i}$
of
$C_{P,i}$
of
![]() $(E_{P,i},\theta _{P,i})$
such that
$(E_{P,i},\theta _{P,i})$
such that
![]() $C_{P,i|X_P^{\ast }}$
is compatible with
$C_{P,i|X_P^{\ast }}$
is compatible with
![]() $(h_{\infty })_{P,i}$
. For
$(h_{\infty })_{P,i}$
. For
![]() $t\gt 0$
, there exists a harmonic metric
$t\gt 0$
, there exists a harmonic metric
![]() $h_{t,P,i}$
of
$h_{t,P,i}$
of
![]() $(E_{P,i},\theta _{P,i})$
which is compatible with
$(E_{P,i},\theta _{P,i})$
which is compatible with
![]() $C_{P,i}$
such that its boundary value at
$C_{P,i}$
such that its boundary value at
![]() ${\partial } X_P$
is equal to that of
${\partial } X_P$
is equal to that of
![]() $h_{\infty |E_{P,i}}$
. We construct the metric
$h_{\infty |E_{P,i}}$
. We construct the metric
![]() $\widetilde{h}_{t}$
by using
$\widetilde{h}_{t}$
by using
![]() $h_{t,P,i}$
as in the proof of Theorem7.5 (see §7.1.3). By Proposition 6.7, the following holds.
$h_{t,P,i}$
as in the proof of Theorem7.5 (see §7.1.3). By Proposition 6.7, the following holds.
Lemma 7.16.
Let
![]() $s(h_{\infty },\widetilde{h}_t)$
be the automorphism of
$s(h_{\infty },\widetilde{h}_t)$
be the automorphism of
![]() $E_{|X\setminus D}$
determined by
$E_{|X\setminus D}$
determined by
![]() $\widetilde{h}_t=h_{\infty }\cdot s(h_{\infty },\widetilde{h}_t)$
. For any relatively compact open subset
$\widetilde{h}_t=h_{\infty }\cdot s(h_{\infty },\widetilde{h}_t)$
. For any relatively compact open subset
![]() $K$
of
$K$
of
![]() $X_P^{\ast }$
and for any
$X_P^{\ast }$
and for any
![]() $\ell \in \mathbb{Z}_{\geqslant 0}$
, there exist constants
$\ell \in \mathbb{Z}_{\geqslant 0}$
, there exist constants
![]() $C(K,\ell ),\epsilon (K,\ell ),t(K)\gt 0$
such that the
$C(K,\ell ),\epsilon (K,\ell ),t(K)\gt 0$
such that the
![]() $L_{\ell }^2$
-norms of
$L_{\ell }^2$
-norms of
![]() $s(h_{\infty },\widetilde{h}_t)-{\mathop{\textrm{id}}\nolimits }$
on
$s(h_{\infty },\widetilde{h}_t)-{\mathop{\textrm{id}}\nolimits }$
on
![]() $K$
with respect to
$K$
with respect to
![]() $h_{\infty }$
and
$h_{\infty }$
and
![]() $g_X$
are dominated by
$g_X$
are dominated by
![]() $C(K,\ell )\exp (-\epsilon (K,\ell )t)$
for any
$C(K,\ell )\exp (-\epsilon (K,\ell )t)$
for any
![]() $t\gt t(K)$
.
$t\gt t(K)$
.
By Lemma 7.16, we obtain
for some
![]() $\epsilon, C\gt 0$
. Moreover, by the construction, the support of (54) is contained in
$\epsilon, C\gt 0$
. Moreover, by the construction, the support of (54) is contained in
Let
![]() $s_t$
be the automorphism of
$s_t$
be the automorphism of
![]() $E$
determined by
$E$
determined by
![]() $h_t=\widetilde{h}_t\cdot s_t$
. We obtain Theorem7.14 from Lemma 7.16 and the following theorem.
$h_t=\widetilde{h}_t\cdot s_t$
. We obtain Theorem7.14 from Lemma 7.16 and the following theorem.
Theorem 7.17.
For any
![]() $\ell \gt 0$
, there exist
$\ell \gt 0$
, there exist
![]() $C(\ell ),\epsilon (\ell )\gt 0$
such that the
$C(\ell ),\epsilon (\ell )\gt 0$
such that the
![]() $L_{\ell }^2$
-norms of
$L_{\ell }^2$
-norms of
![]() $s_t-{\mathop{\textrm{id}}\nolimits }$
on
$s_t-{\mathop{\textrm{id}}\nolimits }$
on
![]() $X$
with respect to
$X$
with respect to
![]() $\widetilde{h}_t$
,
$\widetilde{h}_t$
,
![]() $g_X$
and the Chern connection of
$g_X$
and the Chern connection of
![]() $\widetilde{h}_t$
are dominated by
$\widetilde{h}_t$
are dominated by
![]() $C(\ell )\exp (-\epsilon (\ell ) t)$
.
$C(\ell )\exp (-\epsilon (\ell ) t)$
.
Proof.
By [Reference SimpsonSim88, Lemma 3.1] and (54), there exist
![]() $C_1,\epsilon _1\gt 0$
such that
$C_1,\epsilon _1\gt 0$
such that
By Corollary 7.7,
![]() $|s_{t}|_{\widetilde{h}_{t}}$
and
$|s_{t}|_{\widetilde{h}_{t}}$
and
![]() $|s_{t}^{-1}|_{\widetilde{h}_{t}}$
are uniformly bounded. There exist
$|s_{t}^{-1}|_{\widetilde{h}_{t}}$
are uniformly bounded. There exist
![]() $C_2,\epsilon _2\gt 0$
such that
$C_2,\epsilon _2\gt 0$
such that
Let
![]() $K$
be a relatively compact open subset of
$K$
be a relatively compact open subset of
![]() $X\setminus D$
. By the variant of Simpson’s main estimate ([Reference MochizukiMoc16, Theorem 2.9]) and Lemma 7.16, there exist
$X\setminus D$
. By the variant of Simpson’s main estimate ([Reference MochizukiMoc16, Theorem 2.9]) and Lemma 7.16, there exist
![]() $C_3(K),\epsilon _3(K)\gt 0$
such that the following holds on
$C_3(K),\epsilon _3(K)\gt 0$
such that the following holds on
![]() $K$
:
$K$
:
Together with (55), we obtain that there exist
![]() $C_4(K),\epsilon _4(K)\gt 0$
such that the following holds on
$C_4(K),\epsilon _4(K)\gt 0$
such that the following holds on
![]() $K$
:
$K$
:
Because
![]() $s_{t}$
is self-adjoint with respect to
$s_{t}$
is self-adjoint with respect to
![]() $\widetilde{h}_{t}$
, we obtain the following on
$\widetilde{h}_{t}$
, we obtain the following on
![]() $K$
:
$K$
:
Lemma 7.18.
There exist
![]() $C(K),\epsilon (K)\gt 0$
such that the following holds on
$C(K),\epsilon (K)\gt 0$
such that the following holds on
![]() $K$
:
$K$
:
Proof.
Let
![]() $P$
be any point of
$P$
be any point of
![]() $X\setminus D$
. Let
$X\setminus D$
. Let
![]() $X_P$
be a simply connected neighbourhood of
$X_P$
be a simply connected neighbourhood of
![]() $P$
in
$P$
in
![]() $X\setminus D$
. There exists a decomposition into Higgs bundles of rank
$X\setminus D$
. There exists a decomposition into Higgs bundles of rank
![]() $1$
:
$1$
:
 \begin{align*} (E,\theta )_{|X_P} =\bigoplus _{i=1}^{\mathop {\textrm {rank}}\nolimits (E)} (E_{P,i},\theta _{P,i}). \end{align*}
\begin{align*} (E,\theta )_{|X_P} =\bigoplus _{i=1}^{\mathop {\textrm {rank}}\nolimits (E)} (E_{P,i},\theta _{P,i}). \end{align*}
We obtain the decomposition
![]() $s_{t}=\sum (s_{t})_{j,i}$
, where
$s_{t}=\sum (s_{t})_{j,i}$
, where
![]() $(s_{t})_{j,i}:E_{P,i}\to E_{P,j}$
. By [Reference MochizukiMoc16, Proposition2.3], there exist
$(s_{t})_{j,i}:E_{P,i}\to E_{P,j}$
. By [Reference MochizukiMoc16, Proposition2.3], there exist
![]() $C_5(P),\epsilon _5(P)\gt 0$
such that the following for
$C_5(P),\epsilon _5(P)\gt 0$
such that the following for
![]() $i\neq j$
on
$i\neq j$
on
![]() $X_P$
:
$X_P$
:
By (56) and (57), there exist
![]() $C_6(P),\epsilon _6(P)\gt 0$
such that
$C_6(P),\epsilon _6(P)\gt 0$
such that
Hence, there exist
![]() $C_7(P),\epsilon _7(P)\gt 0$
such that the following holds for any
$C_7(P),\epsilon _7(P)\gt 0$
such that the following holds for any
![]() $P_1,P_2\in X_P$
:
$P_1,P_2\in X_P$
:
Let
![]() $i\neq j$
. There exists a loop
$i\neq j$
. There exists a loop
![]() $\gamma$
in
$\gamma$
in
![]() $X\setminus D$
such that the monodromy of
$X\setminus D$
such that the monodromy of
![]() $\Sigma _{E,\theta }$
along
$\Sigma _{E,\theta }$
along
![]() $\gamma$
exchanges
$\gamma$
exchanges
![]() $E_i$
and
$E_i$
and
![]() $E_j$
. By taking a finite covering of
$E_j$
. By taking a finite covering of
![]() $\gamma$
by relatively compact open subsets and by applying the above consideration, we obtain that there exist
$\gamma$
by relatively compact open subsets and by applying the above consideration, we obtain that there exist
![]() $C_8(P),\epsilon _8(P)\gt 0$
such that the following holds for any
$C_8(P),\epsilon _8(P)\gt 0$
such that the following holds for any
![]() $P_1\in X_P$
:
$P_1\in X_P$
:
By (58), there exist
![]() $C_9(P),\epsilon _9(P)\gt 0$
such that the following holds on
$C_9(P),\epsilon _9(P)\gt 0$
such that the following holds on
![]() $X_P$
:
$X_P$
:
 \begin{align} \left | \prod _{i=1}^{\mathop{\textrm{rank}}\nolimits (E)} (s_{t})_{i,i} -1 \right | \leqslant C_9(P)\exp (-\epsilon _9(P) t). \end{align}
\begin{align} \left | \prod _{i=1}^{\mathop{\textrm{rank}}\nolimits (E)} (s_{t})_{i,i} -1 \right | \leqslant C_9(P)\exp (-\epsilon _9(P) t). \end{align}
By (59) and (60), there exist
![]() $C_{10}(P),\epsilon _{10}(P)\gt 0$
such that
$C_{10}(P),\epsilon _{10}(P)\gt 0$
such that
Then, we obtain the claim of Lemma 7.18.
We obtain the estimate of
![]() $|s_t-{\mathop{\textrm{id}}\nolimits }|_{\widetilde{h}_t}$
around
$|s_t-{\mathop{\textrm{id}}\nolimits }|_{\widetilde{h}_t}$
around
![]() $D$
by using Theorem4.3. We can also obtain the estimate for the higher derivatives by using Theorem4.3.
$D$
by using Theorem4.3. We can also obtain the estimate for the higher derivatives by using Theorem4.3.
7.3 A family case
7.3.1 Setting
Let
![]() $\mathcal{S}$
be a connected complex manifold. Let
$\mathcal{S}$
be a connected complex manifold. Let
![]() $\mathcal{Y}$
be a complex manifold with a proper smooth morphism
$\mathcal{Y}$
be a complex manifold with a proper smooth morphism
![]() $p_1:\mathcal{Y}\to \mathcal{S}$
. Let
$p_1:\mathcal{Y}\to \mathcal{S}$
. Let
![]() $p_2:\mathcal{S}\times X\to \mathcal{S}$
and
$p_2:\mathcal{S}\times X\to \mathcal{S}$
and
![]() $\pi _2:\mathcal{S}\times T^{\ast }X\to \mathcal{S}\times X$
denote the projections. Let
$\pi _2:\mathcal{S}\times T^{\ast }X\to \mathcal{S}\times X$
denote the projections. Let
![]() $\Phi _0:\mathcal{Y}\to \mathcal{S}\times T^{\ast }X$
be a holomorphic map such that
$\Phi _0:\mathcal{Y}\to \mathcal{S}\times T^{\ast }X$
be a holomorphic map such that
![]() $p_1=p_2\circ \pi _2\circ \Phi _0$
. We set
$p_1=p_2\circ \pi _2\circ \Phi _0$
. We set
![]() $\Phi _1=\pi _2\circ \Phi _0$
. We assume the following conditions:
$\Phi _1=\pi _2\circ \Phi _0$
. We assume the following conditions:
-
– each fiber of
 $p_1$
is connected and one
$p_1$
is connected and one
 $1$
-dimensional;
$1$
-dimensional; -
–
 $\Phi _1$
is proper and finite;
$\Phi _1$
is proper and finite; -
– there exists a closed complex analytic hypersurface
 $\mathcal{D}\subset \mathcal{S}\times X$
such that (i)
$\mathcal{D}\subset \mathcal{S}\times X$
such that (i)
 $\mathcal{D}$
is finite over
$\mathcal{D}$
is finite over
 $\mathcal{S}$
, (ii) the induced map
$\mathcal{S}$
, (ii) the induced map
 $\mathcal{Y}\setminus \Phi _1^{-1}(\mathcal{D}) \to (\mathcal{S}\times X)\setminus \mathcal{D}$
is a covering map and (iii)
$\mathcal{Y}\setminus \Phi _1^{-1}(\mathcal{D}) \to (\mathcal{S}\times X)\setminus \mathcal{D}$
is a covering map and (iii)
 $\Phi _0$
induces an injection
$\Phi _0$
induces an injection
 $\mathcal{Y}\setminus \Phi _1^{-1}(\mathcal{D}) \longrightarrow \mathcal{S}\times T^{\ast }X$
.
$\mathcal{Y}\setminus \Phi _1^{-1}(\mathcal{D}) \longrightarrow \mathcal{S}\times T^{\ast }X$
.
We set
![]() $r:=|\Phi _1^{-1}(P)|$
for any
$r:=|\Phi _1^{-1}(P)|$
for any
![]() $P\in (\mathcal{S}\times X)\setminus \mathcal{D}$
. We set
$P\in (\mathcal{S}\times X)\setminus \mathcal{D}$
. We set
![]() $\widetilde{\mathcal{D}}:=\Phi _1^{-1}(\mathcal{D})$
. For any
$\widetilde{\mathcal{D}}:=\Phi _1^{-1}(\mathcal{D})$
. For any
![]() $x\in \mathcal{S}$
, we set
$x\in \mathcal{S}$
, we set
![]() $\mathcal{Y}_x:=p_1^{-1}(x)$
,
$\mathcal{Y}_x:=p_1^{-1}(x)$
,
![]() $\widetilde{\mathcal{D}}_x:=\mathcal{Y}_x\cap \widetilde{\mathcal{D}}$
and
$\widetilde{\mathcal{D}}_x:=\mathcal{Y}_x\cap \widetilde{\mathcal{D}}$
and
![]() $\mathcal{D}_x:=p_2^{-1}(x)\cap \mathcal{D}$
. Let
$\mathcal{D}_x:=p_2^{-1}(x)\cap \mathcal{D}$
. Let
![]() $g(X)$
denote the genus of
$g(X)$
denote the genus of
![]() $X$
. Let
$X$
. Let
![]() $\widetilde{g}$
denote the genus of
$\widetilde{g}$
denote the genus of
![]() $\mathcal{Y}_x$
, which is independent of
$\mathcal{Y}_x$
, which is independent of
![]() $x\in \mathcal{S}$
.
$x\in \mathcal{S}$
.
Let
![]() $\mathcal{L}$
be a line bundle on
$\mathcal{L}$
be a line bundle on
![]() $\mathcal{Y}$
such that
$\mathcal{Y}$
such that
We obtain the locally free
![]() $\mathcal{O}_{\mathcal{S}\times X}$
-module
$\mathcal{O}_{\mathcal{S}\times X}$
-module
![]() $\mathcal{E}=\Phi _{1\ast }\mathcal{L}$
. It is equipped with the relative Higgs field
$\mathcal{E}=\Phi _{1\ast }\mathcal{L}$
. It is equipped with the relative Higgs field
induced by the
![]() $\mathcal{O}_{\mathcal{S}\times T^{\ast }X}$
-action on
$\mathcal{O}_{\mathcal{S}\times T^{\ast }X}$
-action on
![]() $\Phi _{0\ast }\mathcal{L}$
. For any
$\Phi _{0\ast }\mathcal{L}$
. For any
![]() $x\in \mathcal{S}$
, let
$x\in \mathcal{S}$
, let
![]() $(\mathcal{E}_x,\theta _x)$
be the induced Higgs bundle on
$(\mathcal{E}_x,\theta _x)$
be the induced Higgs bundle on
![]() $X\simeq \{x\}\times X$
. We obtain the following lemma by the construction.
$X\simeq \{x\}\times X$
. We obtain the following lemma by the construction.
Lemma 7.19.
Each
![]() $(\mathcal{E}_x,\theta _x)$
is stable of degree
$(\mathcal{E}_x,\theta _x)$
is stable of degree
![]() $0$
.
$0$
.
7.3.2 Statement
We obtain the holomorphic line bundle
![]() $\det (\mathcal{E})$
on
$\det (\mathcal{E})$
on
![]() $\mathcal{S}\times X$
. There exists a
$\mathcal{S}\times X$
. There exists a
![]() $C^{\infty }$
-Hermitian metric
$C^{\infty }$
-Hermitian metric
![]() $h_{\det (\mathcal{E})}$
of
$h_{\det (\mathcal{E})}$
of
![]() $\det (\mathcal{E})$
such that
$\det (\mathcal{E})$
such that
![]() $h_{\det (\mathcal{E}),x}:=h_{\det (\mathcal{E})|\{x\}\times X}$
is flat for any
$h_{\det (\mathcal{E}),x}:=h_{\det (\mathcal{E})|\{x\}\times X}$
is flat for any
![]() $x\in \mathcal{S}$
.
$x\in \mathcal{S}$
.
We have the decomposable filtered Higgs bundle
![]() $(\mathcal{P}^{\star }_{\ast }\mathcal{E}_x,\theta _x)$
on
$(\mathcal{P}^{\star }_{\ast }\mathcal{E}_x,\theta _x)$
on
![]() $(X,\mathcal{D}_{x})$
. Let
$(X,\mathcal{D}_{x})$
. Let
![]() $h_{\infty, x}$
be the decoupled harmonic metric of
$h_{\infty, x}$
be the decoupled harmonic metric of
![]() $(\mathcal{E}_x,\theta _x)_{|X\setminus \mathcal{D}_{x}}$
such that
$(\mathcal{E}_x,\theta _x)_{|X\setminus \mathcal{D}_{x}}$
such that
![]() $\det (h_{\infty, x})=h_{\det (\mathcal{E}),x}$
.
$\det (h_{\infty, x})=h_{\det (\mathcal{E}),x}$
.
Lemma 7.20. The metrics
![]() $h_{\infty, x}$
$h_{\infty, x}$
![]() $(x\in \mathcal{S})$
induce a
$(x\in \mathcal{S})$
induce a
![]() $C^{\infty }$
-metric of
$C^{\infty }$
-metric of
![]() $\mathcal{E}_{|(\mathcal{S}\times X)\setminus \mathcal{D}}$
.
$\mathcal{E}_{|(\mathcal{S}\times X)\setminus \mathcal{D}}$
.
Proof.
It is enough to study locally around any point
![]() $x_0\in \mathcal{S}$
. By using the examples in §6.3.3, we can construct a
$x_0\in \mathcal{S}$
. By using the examples in §6.3.3, we can construct a
![]() $C^{\infty }$
-Hermitian metric
$C^{\infty }$
-Hermitian metric
![]() $h_0$
of
$h_0$
of
![]() $\mathcal{L}_{|\mathcal{Y}\setminus \widetilde{\mathcal{D}}}$
such that (i)
$\mathcal{L}_{|\mathcal{Y}\setminus \widetilde{\mathcal{D}}}$
such that (i)
![]() $h_0$
is flat around
$h_0$
is flat around
![]() $\widetilde{\mathcal{D}}$
and (ii)
$\widetilde{\mathcal{D}}$
and (ii)
![]() $h_{0|\mathcal{Y}_x\setminus \widetilde{\mathcal{D}}_{x}}$
is adapted to
$h_{0|\mathcal{Y}_x\setminus \widetilde{\mathcal{D}}_{x}}$
is adapted to
![]() $\mathcal{P}^{\star }_{\ast }(\mathcal{L}_{|\mathcal{Y}_x})$
. By using Lemma 7.23 below, we can construct a
$\mathcal{P}^{\star }_{\ast }(\mathcal{L}_{|\mathcal{Y}_x})$
. By using Lemma 7.23 below, we can construct a
![]() $C^{\infty }$
-function
$C^{\infty }$
-function
![]() $f$
on
$f$
on
![]() $\mathcal{Y}$
such that
$\mathcal{Y}$
such that
![]() $h_{1,x}=e^{f}h_{0,x}$
$h_{1,x}=e^{f}h_{0,x}$
![]() $(x\in \mathcal{S})$
is a family of flat metrics
$(x\in \mathcal{S})$
is a family of flat metrics
![]() $\mathcal{L}_{|\mathcal{Y}_x\setminus \widetilde{\mathcal{D}}_{x}}$
. It induces a family of decoupled harmonic metrics
$\mathcal{L}_{|\mathcal{Y}_x\setminus \widetilde{\mathcal{D}}_{x}}$
. It induces a family of decoupled harmonic metrics
![]() $h_{2,x}$
of
$h_{2,x}$
of
![]() $(\mathcal{E}_x,\theta _x)_{|X\setminus \mathcal{D}_{x}}$
such that they give a
$(\mathcal{E}_x,\theta _x)_{|X\setminus \mathcal{D}_{x}}$
such that they give a
![]() $C^{\infty }$
-Hermitian metric
$C^{\infty }$
-Hermitian metric
![]() $h_2$
of
$h_2$
of
![]() $\mathcal{E}_{|(\mathcal{S}\times X)\setminus \mathcal{D}}$
. Note that
$\mathcal{E}_{|(\mathcal{S}\times X)\setminus \mathcal{D}}$
. Note that
![]() $\det (h_{2,x})$
induces a flat metric of
$\det (h_{2,x})$
induces a flat metric of
![]() $\det (\mathcal{E}_x,\theta _x)$
. For each
$\det (\mathcal{E}_x,\theta _x)$
. For each
![]() $x\in \mathcal{S}$
, because both
$x\in \mathcal{S}$
, because both
![]() $\det (h_{2,x})$
and
$\det (h_{2,x})$
and
![]() $h_{\det (\mathcal{E}),x}$
are flat metrics of
$h_{\det (\mathcal{E}),x}$
are flat metrics of
![]() $\det (\mathcal{E}_x)$
, we obtain that
$\det (\mathcal{E}_x)$
, we obtain that
![]() $\alpha _x\gt 0$
determined by
$\alpha _x\gt 0$
determined by
![]() $\det (h_{2,x})=\alpha _xh_{\det (\mathcal{E}),x}$
. Because
$\det (h_{2,x})=\alpha _xh_{\det (\mathcal{E}),x}$
. Because
![]() $\det (h_{2,x})$
$\det (h_{2,x})$
![]() $(x\in \mathcal{S})$
give a
$(x\in \mathcal{S})$
give a
![]() $C^{\infty }$
-metric of
$C^{\infty }$
-metric of
![]() $\det (\mathcal{E})_{|(\mathcal{S}\times X)\setminus \mathcal{D}}$
, we obtain that
$\det (\mathcal{E})_{|(\mathcal{S}\times X)\setminus \mathcal{D}}$
, we obtain that
![]() $\alpha _x$
$\alpha _x$
![]() $(x\in \mathcal{S})$
give a
$(x\in \mathcal{S})$
give a
![]() $C^{\infty }$
-function on
$C^{\infty }$
-function on
![]() $\mathcal{S}$
. Because
$\mathcal{S}$
. Because
![]() $h_{\infty, x}=e^{-\alpha _x/r}h_{2,x}$
, we obtain that
$h_{\infty, x}=e^{-\alpha _x/r}h_{2,x}$
, we obtain that
![]() $h_{\infty, x}$
induces a
$h_{\infty, x}$
induces a
![]() $C^{\infty }$
-metric of
$C^{\infty }$
-metric of
![]() $\mathcal{E}_{(\mathcal{S}\times X)\setminus \mathcal{D}}$
.
$\mathcal{E}_{(\mathcal{S}\times X)\setminus \mathcal{D}}$
.
Let
![]() $h_{t,x}$
be a harmonic metric of
$h_{t,x}$
be a harmonic metric of
![]() $(\mathcal{E}_x,t\theta _x)$
such that
$(\mathcal{E}_x,t\theta _x)$
such that
![]() $\det (h_{t,x})=h_{\det (\mathcal{E}),x}$
. Let
$\det (h_{t,x})=h_{\det (\mathcal{E}),x}$
. Let
![]() $(V_x,\theta _x):=(\mathcal{E}_x,\theta _x)_{|X\setminus \mathcal{D}_{x}}$
. We obtain the automorphism
$(V_x,\theta _x):=(\mathcal{E}_x,\theta _x)_{|X\setminus \mathcal{D}_{x}}$
. We obtain the automorphism
![]() $s(h_{\infty, x},h_{t,x})$
of
$s(h_{\infty, x},h_{t,x})$
of
![]() $V_x$
determined by
$V_x$
determined by
![]() $h_{t,x}=h_{\infty, x}\cdot s(h_{\infty, x},h_{t,x})$
.
$h_{t,x}=h_{\infty, x}\cdot s(h_{\infty, x},h_{t,x})$
.
Theorem 7.21.
Let
![]() $x_0\in \mathcal{S}$
. Let
$x_0\in \mathcal{S}$
. Let
![]() $K$
be any relatively compact open subset in
$K$
be any relatively compact open subset in
![]() $X\setminus \mathcal{D}_{x_0}$
. Let
$X\setminus \mathcal{D}_{x_0}$
. Let
![]() $\mathcal{S}_0$
be a neighbourhood of
$\mathcal{S}_0$
be a neighbourhood of
![]() $x_0$
such that
$x_0$
such that
![]() $\mathcal{S}_0\times K$
is relatively compact in
$\mathcal{S}_0\times K$
is relatively compact in
![]() $(\mathcal{S}\times X)\setminus \mathcal{D}$
. For any
$(\mathcal{S}\times X)\setminus \mathcal{D}$
. For any
![]() $\ell \in \mathbb{Z}_{\geqslant 0}$
, there exist positive constants
$\ell \in \mathbb{Z}_{\geqslant 0}$
, there exist positive constants
![]() $C(\ell, K)$
and
$C(\ell, K)$
and
![]() $\epsilon (\ell, K)$
such that the
$\epsilon (\ell, K)$
such that the
![]() $L_{\ell }^2$
-norms of
$L_{\ell }^2$
-norms of
![]() $s(h_{\infty, x},h_{t,x})-{\mathop{\textrm{id}}\nolimits }$
$s(h_{\infty, x},h_{t,x})-{\mathop{\textrm{id}}\nolimits }$
![]() $(x\in \mathcal{S}_0,t\geqslant 1)$
on
$(x\in \mathcal{S}_0,t\geqslant 1)$
on
![]() $K$
with respect to
$K$
with respect to
![]() $h_{\infty, x}$
,
$h_{\infty, x}$
,
![]() $g_X$
and the Chern connection of
$g_X$
and the Chern connection of
![]() $h_{\infty, x}$
are dominated by
$h_{\infty, x}$
are dominated by
![]() $C(\ell, K)\exp (-\epsilon (\ell, K)t)$
.
$C(\ell, K)\exp (-\epsilon (\ell, K)t)$
.
7.3.3 Refined statement
Let
![]() $x_0\in \mathcal{S}$
. For any
$x_0\in \mathcal{S}$
. For any
![]() $P\in \mathcal{D}_{x_0}$
, let
$P\in \mathcal{D}_{x_0}$
, let
![]() $(U_P,z_P)$
be a simply connected holomorphic coordinate neighbourhood of
$(U_P,z_P)$
be a simply connected holomorphic coordinate neighbourhood of
![]() $P$
in
$P$
in
![]() $X$
such that
$X$
such that
![]() $U_P\cap \mathcal{D}_{x_0}=\{P\}$
and that
$U_P\cap \mathcal{D}_{x_0}=\{P\}$
and that
![]() $z_P$
induces
$z_P$
induces
![]() $(U_P,P)\simeq (B(2),0)$
. Moreover, we assume that
$(U_P,P)\simeq (B(2),0)$
. Moreover, we assume that
![]() $z_P$
induces a holomorphic isomorphism between neighbourhoods of the closures of
$z_P$
induces a holomorphic isomorphism between neighbourhoods of the closures of
![]() $U_P$
and
$U_P$
and
![]() $B(2)$
. Let
$B(2)$
. Let
![]() $\mathcal{S}_{1,P}$
be a relatively compact open neighbourhood of
$\mathcal{S}_{1,P}$
be a relatively compact open neighbourhood of
![]() $x_0$
in
$x_0$
in
![]() $\mathcal{S}$
such that
$\mathcal{S}$
such that
Let
![]() $\mathcal{S}_1$
be a connected open neighbourhood of
$\mathcal{S}_1$
be a connected open neighbourhood of
![]() $x_0$
in
$x_0$
in
![]() $\bigcap _{P\in \mathcal{D}_{x_0}}\mathcal{S}_{1,P}$
.
$\bigcap _{P\in \mathcal{D}_{x_0}}\mathcal{S}_{1,P}$
.
For
![]() $P\in \mathcal{D}_{x_0}$
and
$P\in \mathcal{D}_{x_0}$
and
![]() $x\in \mathcal{S}_1$
, let
$x\in \mathcal{S}_1$
, let
![]() $h_{t,P,x}$
be the harmonic metric of
$h_{t,P,x}$
be the harmonic metric of
![]() $(\mathcal{E}_x,\theta _x)_{|\{|z_P|\lt 1\}}$
such that
$(\mathcal{E}_x,\theta _x)_{|\{|z_P|\lt 1\}}$
such that
![]() $h_{t,P,x|\{|z_P|=1\}} =h_{\infty, x|\{|z_P|=1\}}$
. We note that Condition 6.17 is satisfied for
$h_{t,P,x|\{|z_P|=1\}} =h_{\infty, x|\{|z_P|=1\}}$
. We note that Condition 6.17 is satisfied for
![]() $h_{\infty, x|U_P}$
by Lemma 7.15, and we can apply Proposition 6.18 to
$h_{\infty, x|U_P}$
by Lemma 7.15, and we can apply Proposition 6.18 to
![]() $h_{t,P,x}$
. We construct Hermitian metrics
$h_{t,P,x}$
. We construct Hermitian metrics
![]() $\widetilde{h}_{t,x}$
of
$\widetilde{h}_{t,x}$
of
![]() $\mathcal{E}_{x}$
$\mathcal{E}_{x}$
![]() $(x\in \mathcal{S}_1)$
from
$(x\in \mathcal{S}_1)$
from
![]() $h_{\infty, x}$
and
$h_{\infty, x}$
and
![]() $h_{t,P,x}$
$h_{t,P,x}$
![]() $(P\in \mathcal{D}_{x_0})$
as in §7.1.3. Let
$(P\in \mathcal{D}_{x_0})$
as in §7.1.3. Let
![]() $s(\widetilde{h}_{t,x},h_{t,x})$
be the automorphism of
$s(\widetilde{h}_{t,x},h_{t,x})$
be the automorphism of
![]() $\mathcal{E}_x$
determined by
$\mathcal{E}_x$
determined by
![]() $h_{t,x}=\widetilde{h}_{t,x}\cdot s(\widetilde{h}_{t,x},h_{t,x})$
. By using Proposition 6.18, we obtain the following theorem in the same way as Theorem7.14, which implies Theorem7.21.
$h_{t,x}=\widetilde{h}_{t,x}\cdot s(\widetilde{h}_{t,x},h_{t,x})$
. By using Proposition 6.18, we obtain the following theorem in the same way as Theorem7.14, which implies Theorem7.21.
Theorem 7.22.
For any
![]() $\ell \in \mathbb{Z}_{\geqslant 0}$
, there exist positive constants
$\ell \in \mathbb{Z}_{\geqslant 0}$
, there exist positive constants
![]() $C(\ell )$
and
$C(\ell )$
and
![]() $\epsilon (\ell )$
such that the
$\epsilon (\ell )$
such that the
![]() $L^{2}_{\ell }$
-norms of
$L^{2}_{\ell }$
-norms of
with respect to
![]() $\widetilde{h}_{t,x}$
,
$\widetilde{h}_{t,x}$
,
![]() $g_X$
and
$g_X$
and
![]() $\widetilde{h}_{t,x}$
are dominated by
$\widetilde{h}_{t,x}$
are dominated by
![]() $C(\ell )\exp (-\epsilon (\ell )t)$
.
$C(\ell )\exp (-\epsilon (\ell )t)$
.
7.3.4 Appendix
Let
![]() $M$
be a compact oriented
$M$
be a compact oriented
![]() $C^{\infty }$
-manifold. Let
$C^{\infty }$
-manifold. Let
![]() $S$
be a
$S$
be a
![]() $C^{\infty }$
-manifold. Let
$C^{\infty }$
-manifold. Let
![]() $g_{S\times M}$
be a Riemannian metric of
$g_{S\times M}$
be a Riemannian metric of
![]() $S\times M$
. For each
$S\times M$
. For each
![]() $x\in S$
, we set
$x\in S$
, we set
![]() $M_x:=\{x\}\times M$
. Let
$M_x:=\{x\}\times M$
. Let
![]() $g_x$
and
$g_x$
and
![]() $\Delta _x$
denote the induced Riemannian metric and the associated Laplacian of
$\Delta _x$
denote the induced Riemannian metric and the associated Laplacian of
![]() $M_x$
.
$M_x$
.
Lemma 7.23.
Let
![]() $f_1$
be a
$f_1$
be a
![]() $C^{\infty }$
-function on
$C^{\infty }$
-function on
![]() $S\times M$
such that
$S\times M$
such that
![]() $\int _{M_x} f_{1}\mathop{\textrm{dvol}}\nolimits _{g_x}=0$
. Let
$\int _{M_x} f_{1}\mathop{\textrm{dvol}}\nolimits _{g_x}=0$
. Let
![]() $f_2$
be a function on
$f_2$
be a function on
![]() $S\times M$
determined by the conditions
$S\times M$
determined by the conditions
![]() $\Delta _x(f_{2|M_x})=f_{1|M_x}$
and
$\Delta _x(f_{2|M_x})=f_{1|M_x}$
and
![]() $\int _{M_x}f_{2|M_x}\mathop{\textrm{dvol}}\nolimits _{g_x}=0$
. Then,
$\int _{M_x}f_{2|M_x}\mathop{\textrm{dvol}}\nolimits _{g_x}=0$
. Then,
![]() $f_2$
is
$f_2$
is
![]() $C^{\infty }$
.
$C^{\infty }$
.
Proof.
We explain only a sketch of a proof. For any
![]() $x\in S$
, let
$x\in S$
, let
![]() $f_{i,x}:=f_{i|M_x}$
. Let
$f_{i,x}:=f_{i|M_x}$
. Let
![]() $S_0$
be a relatively compact open subset in
$S_0$
be a relatively compact open subset in
![]() $S$
. There exists a uniform lower bound of the first non-zero eigenvalue of the operators
$S$
. There exists a uniform lower bound of the first non-zero eigenvalue of the operators
![]() $\Delta _{x}$
$\Delta _{x}$
![]() $(x\in S_0)$
(see [Reference LiLi12, Theorem 5.7]). There exists
$(x\in S_0)$
(see [Reference LiLi12, Theorem 5.7]). There exists
![]() $C_0\gt 0$
such that
$C_0\gt 0$
such that
![]() $\|f_{1,x}\|_{L^2}\leqslant C_0$
$\|f_{1,x}\|_{L^2}\leqslant C_0$
![]() $(x\in S_0)$
. By
$(x\in S_0)$
. By
![]() $\Delta _x(f_{1,x})=f_{2,x}$
, for any
$\Delta _x(f_{1,x})=f_{2,x}$
, for any
![]() $\ell \in \mathbb{Z}_{\geqslant 0}$
there exists
$\ell \in \mathbb{Z}_{\geqslant 0}$
there exists
![]() $C_1(\ell )\gt 0$
such that
$C_1(\ell )\gt 0$
such that
![]() $\|f_{1,x}\|_{L^2_{\ell }}\leqslant C_1(\ell )$
for any
$\|f_{1,x}\|_{L^2_{\ell }}\leqslant C_1(\ell )$
for any
![]() $x\in S_0$
. Let
$x\in S_0$
. Let
![]() $x(i)\in S_0$
be a sequence convergent to
$x(i)\in S_0$
be a sequence convergent to
![]() $x(\infty )\in S_0$
. There exists a subsequence
$x(\infty )\in S_0$
. There exists a subsequence
![]() $x'(j)$
convergent to
$x'(j)$
convergent to
![]() $x(\infty )$
such that the sequence
$x(\infty )$
such that the sequence
![]() $f_{1,x^{\prime}(j)}$
is weakly convergent in
$f_{1,x^{\prime}(j)}$
is weakly convergent in
![]() $L_{\ell }^2$
for any
$L_{\ell }^2$
for any
![]() $\ell \in \mathbb{Z}_{\geqslant 0}$
. The limit
$\ell \in \mathbb{Z}_{\geqslant 0}$
. The limit
![]() $f_{\infty }$
satisfies
$f_{\infty }$
satisfies
![]() $\Delta (f_{\infty })=f_{2,x(\infty )}$
and
$\Delta (f_{\infty })=f_{2,x(\infty )}$
and
![]() $\int _{M_{x(\infty )}}f_{\infty }\mathop{\textrm{dvol}}\nolimits _{g_{x(\infty )}}=0$
. We obtain
$\int _{M_{x(\infty )}}f_{\infty }\mathop{\textrm{dvol}}\nolimits _{g_{x(\infty )}}=0$
. We obtain
![]() $f_{\infty }=f_{1,x(\infty )}$
. Hence,
$f_{\infty }=f_{1,x(\infty )}$
. Hence,
![]() $f_{1,x}$
and their derivatives in the
$f_{1,x}$
and their derivatives in the
![]() $M$
-direction are continuous with respect to
$M$
-direction are continuous with respect to
![]() $x\in S$
.
$x\in S$
.
Let
![]() $S_1$
be a relatively compact open subset of
$S_1$
be a relatively compact open subset of
![]() $S$
equipped with a real coordinate system
$S$
equipped with a real coordinate system
![]() $(x_1,\ldots, x_n)$
. Let
$(x_1,\ldots, x_n)$
. Let
![]() $[{\partial }_{j},\Delta _x]$
be the differential operator on
$[{\partial }_{j},\Delta _x]$
be the differential operator on
![]() $S_1\times M$
defined by
$S_1\times M$
defined by
![]() $[{\partial }_{j},\Delta _x](f)={\partial }_{j}(\Delta _x(f))-\Delta _x({\partial }_{j}f)$
. It does not contain a derivative in the
$[{\partial }_{j},\Delta _x](f)={\partial }_{j}(\Delta _x(f))-\Delta _x({\partial }_{j}f)$
. It does not contain a derivative in the
![]() $S_1$
-direction. Note that
$S_1$
-direction. Note that
![]() $[{\partial }_{j},\Delta _x](f_{1,x})$
and their derivative in the
$[{\partial }_{j},\Delta _x](f_{1,x})$
and their derivative in the
![]() $M$
-direction are continuous with respect to
$M$
-direction are continuous with respect to
![]() $x\in S_1$
. Let
$x\in S_1$
. Let
![]() $f_{1,x}^{(j)}$
be the solution of the conditions
$f_{1,x}^{(j)}$
be the solution of the conditions
![]() $\Delta _{x}(f^{(j)}_{1,x}) ={\partial }_{j}f_{2,x}-[{\partial }_{j},\Delta _x]f_{1,x}$
and
$\Delta _{x}(f^{(j)}_{1,x}) ={\partial }_{j}f_{2,x}-[{\partial }_{j},\Delta _x]f_{1,x}$
and
![]() $\int _{M_{x}}f^{(j)}_{1,x}\;\mathop{\textrm{dvol}}\nolimits _{g_{x}}=0$
. Choose
$\int _{M_{x}}f^{(j)}_{1,x}\;\mathop{\textrm{dvol}}\nolimits _{g_{x}}=0$
. Choose
![]() $y=(y_1,\ldots, y_n)\in S_1$
. We define functions
$y=(y_1,\ldots, y_n)\in S_1$
. We define functions
![]() $F^{(j)}_x$
on
$F^{(j)}_x$
on
![]() $M_x$
by
$M_x$
by
![]() $F^{(j)}_{x}=(x_j-y_j)^{-1}(f_{1,x}-f_{1,y})$
if
$F^{(j)}_{x}=(x_j-y_j)^{-1}(f_{1,x}-f_{1,y})$
if
![]() $x_j\neq y_j$
, and
$x_j\neq y_j$
, and
![]() $F^{(j)}_x=f^{(j)}_{1,x}$
if
$F^{(j)}_x=f^{(j)}_{1,x}$
if
![]() $x_j=y_j$
. They satisfy
$x_j=y_j$
. They satisfy
![]() $\Delta _x(F_x^{(j)}) =(x_j-y_j)^{-1}(f_{2,x}-f_{2,y}-(\Delta _x-\Delta _y)f_{1,y})$
if
$\Delta _x(F_x^{(j)}) =(x_j-y_j)^{-1}(f_{2,x}-f_{2,y}-(\Delta _x-\Delta _y)f_{1,y})$
if
![]() $x_j\neq y_j$
and
$x_j\neq y_j$
and
![]() $\Delta _x(F_x^{(j)})={\partial }_jf_{2,x}-[{\partial }_j,\Delta _x]f_{1,x}$
if
$\Delta _x(F_x^{(j)})={\partial }_jf_{2,x}-[{\partial }_j,\Delta _x]f_{1,x}$
if
![]() $x_j=y_j$
. Then, by an argument in the previous paragraph, we can prove that
$x_j=y_j$
. Then, by an argument in the previous paragraph, we can prove that
![]() $F^{(j)}_x$
and their derivatives in the
$F^{(j)}_x$
and their derivatives in the
![]() $M$
-direction are continuous with respect to
$M$
-direction are continuous with respect to
![]() $x$
. This implies that
$x$
. This implies that
![]() $f_{1,x}$
is
$f_{1,x}$
is
![]() $C^1$
-with respect to
$C^1$
-with respect to
![]() $x$
and that
$x$
and that
![]() ${\partial }_jf_{1,x}=f^{(j)}_{1,x}$
. By a similar argument, we can prove that
${\partial }_jf_{1,x}=f^{(j)}_{1,x}$
. By a similar argument, we can prove that
![]() $f_{1,x}$
and their derivatives in the
$f_{1,x}$
and their derivatives in the
![]() $M$
-direction are
$M$
-direction are
![]() $C^{\infty }$
with respect to
$C^{\infty }$
with respect to
![]() $x$
.
$x$
.
Acknowledgements
Both authors are grateful to Laura Fredrickson for the answer to our question related to Remark 1.2. They thank the reviewer for his/her careful reading and helpful suggestions to improve this manuscript. T.M. thanks Qiongling Li for discussions and collaborations. In particular, the ideas in §3 are variants of those in [Reference Li and MochizukiLM10a, Reference Li and MochizukiLM10b]. T.M. is grateful to Rafe Mazzeo and Siqi He for some discussion. Sz.Sz. would like to thank Olivia Dumitrescu and Richard Wentworth for inspiring discussions.
Conflicts of Interest
None.
Financial Support
T. M. is partially supported by the Grant-in-Aid for Scientific Research (A) (No. 21H04429), the Grant-in-Aid for Scientific Research (A) (No. 22H00094), the Grant-in-Aid for Scientific Research (A) (No. 23H00083) and the Grant-in-Aid for Scientific Research (C) (No. 20K03609), from the Japan Society for the Promotion of Science. This work was partially supported by the Research Institute for Mathematical Sciences, an International Joint Usage/Research Center located in Kyoto University. Sz.Sz. was supported by a Lendület Low Dimensional Topology grant from the Hungarian Academy of Sciences and by the grants K120697 and KKP126683 from NKFIH. Sz.Sz. partially enjoyed the hospitality of the Max Planck Institute for Mathematics (Bonn).
Journal Information
Moduli is published as a joint venture of the Foundation Compositio Mathematica and the London Mathematical Society. As not-for-profit organisations, the Foundation and Society reinvest
![]() $100\%$
of any surplus generated from their publications back into mathematics through their charitable activities.
$100\%$
of any surplus generated from their publications back into mathematics through their charitable activities.