Hostname: page-component-669899f699-2mbcq Total loading time: 0 Render date: 2025-04-30T10:38:12.713Z Has data issue: false hasContentIssue false
  • English
  • Français

The distribution of integral and prime-integral values of systems of full-norm polynomials and affine-decomposable polynomials

Published online by Cambridge University Press:  26 February 2010

R. W. K. Odoni
R. W. K. Odoni
Affiliation:
Department of Mathematics, University of Exeter, U.K.
Get access

Extract

Let K be any finite (possibly trivial) extension of ℚ, the field of rational numbers. Let 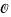denote the ring of integers of K, and let M ⊆ 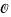be a full module in K thus a free ℤ-module of rank [K : ℚ] contained in 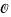; ℤ denoting the ring of rational integers. Regarding 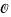as an abelian group, the index (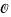: M) is finite. Suppose that m1, …, mk is a ℤ-basis for M and let a ∊ 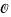Then the polynomial

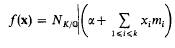
(the xi; being indeterminates) will be called a full-norm polynomial; here NK/ℚ denotes the norm mapping from K to ℚ. Apart from constant factors, such a polynomial f(x) is necessarily irreducible in ℤ[x].

Type
Research Article
Information
Mathematika , Volume 26 , Issue 1 , June 1979 , pp. 80 - 87
Copyright
Copyright © University College London 1979

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

1.Stouff, X.. Annales Fac. Sci. Toulouse (2), 5 (1903), 129–155.Google Scholar
2.Landau, E.. “Ueber die Verteilung der Primideale…”, Math, Annalen, 63 (1907), 145–204.CrossRefGoogle Scholar
3.Hecke, E.. “Ueber die L-Funktionen und den Dirichletschen Primzahlsatz…”, reprinted in Mathematische Werke (2° ed) (Vandenhoeck and Ruprecht, Göttingen, 1970).Google Scholar
4.Odoni, R. W. K.. “Some global norm density results from an extended Cebotarev density theorem”, Algebraic Number Fields (ed. Fröhlich, ) (Academic Press, 1977), 485–495.Google Scholar
5.Landau, E.. Handbuch der Primzahlverteilung (Teubner, Leipzig, 1909), Band 2, 643.Google Scholar
6.Bernays, P.. “Ueber die Darstellung…durch primitiven binären quadratischen Formen”, Dissertation, (Göttingen, 1912).Google Scholar
7.Odoni, R. W. K.. “On the norms of algebraic integers”, Mathematika, 22 (1975), 71–80.CrossRefGoogle Scholar
8.Odoni, R. W. K.. “On norms of integers in a full module…”, Mathematika, 22 (1975), 108–111.Google Scholar
9.Odoni, R. W. K.. “Three problems of Serre on asymptotic properties of coefficients of modular forms of type (1, ξ) on ┌0(N)” (to appear. Proc. hand. Math. Soc).Google Scholar
10.Hasse, H.. “Bericht uber neuere Untersuchungen…”, Physica Verlag. Würzburg-Wien (1970).Google Scholar
11.Artin, E.. Collected papers (ed. Lang, and Tate, ) (Addison-Wesley, Reading, Mass., 1965), 122, Satz 4. Artin's Satz 4 is modulo a hypothesis proved in [12].CrossRefGoogle Scholar
12.Cebotarev, N. G.. “Die Bestimmung der Dichtigkeit…”, Math. Annalen 95 (1925/6), 191–228.Google Scholar