Hostname: page-component-669899f699-8p65j Total loading time: 0 Render date: 2025-04-29T19:13:21.060Z Has data issue: false hasContentIssue false
  • English
  • Français

The order-K-ification monads

Published online by Cambridge University Press:  21 December 2023

Huijun Hou ,
Hualin Miao  and
Qingguo Li Open the ORCID record for Qingguo Li [Opens in a new window]
Huijun Hou
Affiliation:
School of Mathematics, Hunan University, Changsha, Hunan, China
Hualin Miao
Affiliation:
School of Mathematics, Hunan University, Changsha, Hunan, China
Qingguo Li*
Affiliation:
School of Mathematics, Hunan University, Changsha, Hunan, China
*
Corresponding author: Qingguo Li; Email: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Monads prove to be useful mathematical tools in theoretical computer science, notably in denoting different effects of programming languages. In this paper, we investigate a type of monads which arise naturally from Keimel and Lawson’s 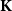$\mathbf{K}$-ification.

A subcategory of 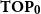$\mathbf{TOP}_{\mathbf{0}}$ is called of type 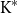$\mathrm{K}^{*}$ if it consists of monotone convergence spaces and is of type 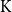$\mathrm K$ in the sense of Keimel and Lawson. Each such category induces a canonical monad 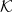$\mathcal K$ on the category 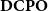$\mathbf{DCPO}$ of dcpos and Scott-continuous maps, which is called the order-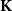$\mathbf{K}$-ification monad in this paper. First, for each category of type 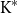$\mathrm{K}^{*}$, we characterize the algebras of the corresponding monad 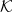$\mathcal K$ as k-complete posets and algebraic homomorphisms as k-continuous maps, from which we obtain that the order-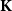$\mathbf{K}$-ification monad gives the free k-complete poset construction over the category $\mathbf{POS}_{\mathbf{d}}$ of posets and Scott-continuous maps. In addition, we show that all k-complete posets and Scott-continuous maps form a Cartesian closed category. Moreover, we consider the strongness of the order-K-ification monad and conclude with the fact that each order-K-ification monad is always commutative.

Keywords

dcposorder-K-ification monadEilenberg-Moore algebrask-complete posets
Type
Paper
Information
Mathematical Structures in Computer Science , Volume 34 , Issue 1 , January 2024 , pp. 45 - 62
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

Footnotes

*This work is supported by the National Natural Science Foundation of China (No.12231007).

References

Borceux, F. (1994). Handbook of Categorical Algebra: Volume 2, Categories and Structures , Encyclopedia of Mathematics and Its Applications, Cambridge, Cambridge University Press.Google Scholar
Eilenberg, S. and Moore, J. (1965). Adjoint functors and triples. Illinois Journal of Mathematics 9 381–398.CrossRefGoogle Scholar
Ershov, Y. L. (2022). K-Completions of T 0-spaces. Algebra and Logic 61 177–187.CrossRefGoogle Scholar
Ershov, Y. L. (1999). On d-spaces. Theoretical Computer Science 224 59–72.CrossRefGoogle Scholar
Escardó, M. (1998). Properly injective spaces and function spaces. Topology and its Applications 89 75–120.CrossRefGoogle Scholar
Gierz, G., Hofmann, K., Keimel, K., Lawson, J., Mislove, M. and Scott, D. (2003). Continuous lattices and domains. In: Encyclopedia of Mathematics and its Applications, Cambridge, Cambridge University Press.CrossRefGoogle Scholar
Goubault-Larrecq, J. (2013). Non-Hausdorff Topology and Domain Theory , New Mathematical Monographs, Cambridge, Cambridge University Press.Google Scholar
Hennessy, M. and Plotkin, G. (1979). Full abstraction for a simple parallel programming language. In: International Symposium on Mathematical Foundations of Computer Science, Berlin, Heidelberg, Springer, 108–120.Google Scholar
Ho, W., Goubault-Larrecq, J., Jung, A. and Xi, X. (2018). The Ho-Zhao problem. Logical Methods in Computer Science 14 1–19.Google Scholar
Jia, X. (2020). The order-sobrification monad. Applied Categorical Structures 28 845–852.CrossRefGoogle Scholar
Jia, X., Kornell, A., Lindenhovius, B., Mislove, M. and Zamdzhiev, V. (2022). Semantics for variational quantum programming. Proceedings of the ACM on Programming Languages 6 (POPL) 1–31.CrossRefGoogle Scholar
Jia, X., Lindenhovius, B., Mislove, M. and Zamdzhiev, V. Commutative monads for probabilistic programming languages. In: In the Proceedings of the 36th Annual ACM/IEEE Symposium on Logic in Computer Science, (LICS2021), 1–14.CrossRefGoogle Scholar
Jia, X. and Mislove, M. (2022). Completing simple valuations in K-categories. Topology and its Applications 318 108192.CrossRefGoogle Scholar
Jung, A. (1989). Cartesian Closed Categories of Domains, Amsterdam, Centrum voor Wiskunde en Informatica.Google Scholar
Keimel, K. and Lawson, J. (2009). D-completions and the d-topology. Annals of Pure and Applied Logic 159 292–306.CrossRefGoogle Scholar
Kock, A. (1970). Monads on symmetric monoidal closed categories. Archiv der Mathematik 21 1–10.CrossRefGoogle Scholar
Kock, A. (1972). Strong functors and monoidal monads. Archiv der Mathematik 23 113–120.CrossRefGoogle Scholar
Lambek, J. (1985). Cartesian closed categories and typed λ-calculi. In: LITP Spring School on Theoretical Computer Science, Berlin, Heidelberg, Springer Berlin Heidelberg, 136–175.Google Scholar
Liu, B., Li, Q. and Wu, G. (2020). Well-filterifications of topological spaces. Topology and its Applications 279 107245.CrossRefGoogle Scholar
Mac Lane, S. (1998). Categories for the Working Mathematician , Graduate Texts in Mathematics, vol. 5, Berlin, Springer.Google Scholar
Moggi, E. (1989). Computational lambda-calculus and monads. In: 4th Symposium on Logic in Computer Science, 14–23.CrossRefGoogle Scholar
Moggi, E. (1991). Notions of computation and monads. Information and Computation 93 55–92.CrossRefGoogle Scholar
Plotkin, G. (1976). A powerdomain construction. SIAM Journal on Computing 5 452–487.CrossRefGoogle Scholar
Plotkin, G. and Power, J. (2001). Adequacy for algebraic effects. In: International Conference on Foundations of Software Science and Computation Structures, Berlin, Heidelberg, Springer Berlin Heidelberg, 1–24.CrossRefGoogle Scholar
Schalk, A. (1993). Algebras for Generalized Power Constructions. Phd thesis, Technische Hochschule Darmstadt.Google Scholar
Scott, D. (1976). Data types as lattices. SIAM Journal on computing 5 (3) 522–587.CrossRefGoogle Scholar
Shen, C., Xi, X., Xu, X. and Zhao, D. (2019). On well-filtered reflections of T 0 spaces. Topology and its Applications 267 106869.CrossRefGoogle Scholar
Shen, C., Xi, X. and Zhao, D. (2021). The reflectivity of some categories of T 0 spaces in domain theory. arXiv e-prints.Google Scholar
Smyth, M. (1976). Powerdomains. In: International Symposium on Mathematical Foundations of Computer Science, Berlin, Heidelberg, Springer, 537–543.Google Scholar
Streicher, T. (2006). Domain-Theoretic Foundations of Functional Programming, Singapore, World Scientific Publishing Company.CrossRefGoogle Scholar
Wu, G., Xi, X., Xu, X. and Zhao, D. (2020). Existence of well-filterifications of T 0 topological spaces. Topology and its Applications 270 107044.CrossRefGoogle Scholar
Wyler, O. (1979). Dedekind complete posets and Scott topologies. In: Lecture Notes in Mathematics, Berlin, Heidelberg, Springer, vol. 871, 384–389.Google Scholar
Xi, X. and Lawson, J. (2017). On well-filtered spaces and ordered sets. Topology and its Applications 228 139–144.CrossRefGoogle Scholar
Xu, X. (2020). A direct approach to K-reflections of T 0 spaces. Topology and its Applications 272 107076.CrossRefGoogle Scholar
Xu, X., Shen, C., Xi, X. and Zhao, D. (2020). First countability, ω-well-filtered spaces and reflections. Topology and its Applications 279 107255.CrossRefGoogle Scholar
Xu, X. and Zhao, D. (2020). On topological Rudin’s lemma, well-filtered spaces and sober spaces. Topology and its Applications 272 107080.CrossRefGoogle Scholar
Zhang, Z. and Li, Q. (2017). A direct characterization of the monotone convergence space completion. Topology and its Applications 230 99–104.CrossRefGoogle Scholar
Zhao, D. and Fan, T. (2010). Dcpo-completion of posets. Theoretical Computer Science 411 2167–2173.CrossRefGoogle Scholar