Hostname: page-component-669899f699-7tmb6 Total loading time: 0 Render date: 2025-04-30T03:19:40.067Z Has data issue: false hasContentIssue false
  • English
  • Français

Elementary quantum recursion schemes that capture quantum polylogarithmic-time computability of quantum functions

Published online by Cambridge University Press:  22 November 2024

Tomoyuki Yamakami Open the ORCID record for Tomoyuki Yamakami [Opens in a new window]
Tomoyuki Yamakami*
Affiliation:
Faculty of Engineering, University of Fukui, Fukui, Japan
*
Email: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Quantum computing has been studied over the past four decades based on two computational models of quantum circuits and quantum Turing machines. To capture quantum polynomial-time computability, a new recursion-theoretic approach was taken lately by Yamakami [J. Symb. Logic 80, pp. 1546–1587, 2020] by way of recursion schematic definition, which constitutes six initial quantum functions and three construction schemes of composition, branching, and multi-qubit quantum recursion. By taking a similar approach, we look into quantum polylogarithmic-time computability and further explore the expressing power of elementary schemes designed for such quantum computation. In particular, we introduce an elementary form of the quantum recursion, called the fast quantum recursion, and formulate 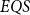$EQS$ (elementary quantum schemes) of “elementary” quantum functions. This class 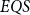$EQS$ captures exactly quantum polylogarithmic-time computability, which forms the complexity class BQPOLYLOGTIME. We also demonstrate the separation of BQPOLYLOGTIME from NLOGTIME and PPOLYLOGTIME. As a natural extension of 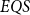$EQS$, we further consider an algorithmic procedural scheme that implements the well-known divide-and-conquer strategy. This divide-and-conquer scheme helps compute the parity function, but the scheme cannot be realized within our system $EQS$.

Keywords

Recursion schematic definitionquantum Turing machinefast quantum recursionquantum polylogarithmic-time computabilitydivide-and-conquer strategy
Type
Special Issue: WoLLIC 2022
Information
Mathematical Structures in Computer Science , Volume 34 , Special Issue 7: WoLLIC 2022 , August 2024 , pp. 710 - 745
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

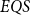Footnotes

aA preliminary report (Yamakami, 2022b) has appeared under a slightly different title in the Proceedings of the 28th International Conference on Logic, Language, Information, and Computation (WoLLIC 2022), Iaşi, Romania, September 20–23, 2022, Lecture Notes in Computer Science, vol. 13468, pp. 88–104, Springer, 2022.

References

Ambainis, A. (2002). Quantum lower bounds by quantum arguments. Journal of Computer and System Sciences 64 (4) 750–767.CrossRefGoogle Scholar
Babai, L., Fortnow, L., Levin, L. A. and Szegedy, M. (1991). Checking computations in polylogarithmic time. In: Proceedings of the 23rd Annual ACM Symposium on Theory of Computing (STOC’91), 21–31.CrossRefGoogle Scholar
Barenco, A., Bennett, C. H., Cleve, R., DiVicenzo, D., Margolus, N., Shor, P., Sleator, T., Smolin, J. and Weinfurter, H. (1995). Elementary gates for quantum computation. Physical Review A. 52 (5) 3457–3467.CrossRefGoogle ScholarPubMed
Barrington, D. A. M., Immerman, N. and Straubing, H. (1990). On uniformity within NC1. Journal of Computer and System Sciences. 41 274–306.CrossRefGoogle Scholar
Beals, R., Buhrman, H., Cleve, R., Mosca, M. and de Wolf, R. (2001). Quantum lower bounds by polynomials. Journal of the ACM. 48 (4) 778–797.CrossRefGoogle Scholar
Benioff, P. (1980). The computer as a physical system: a microscopic quantum mechanical Hamiltonian model of computers as represented by Turing machines. Journal of Statistical Physics. 22 (5) 563–591.CrossRefGoogle Scholar
Bernstein, E. and Vazirani, U. (1997). Quantum complexity theory. SIAM Journal on Computing. 26 (5) 1411–1473.CrossRefGoogle Scholar
Bradford, P. G., Rawlins, G. J. E. and Shannon, G. E. (1994). Efficent matrix chain ordering in polylog time. In: Proceedings of the 8th International Symposium on Parallel Processing, IEEE Computer Society, 234–241.Google Scholar
Buss, S. (1987). The Boolean formula value problem is in ALOGTIME. In: Proceedings of the 19th Annual ACM Symposium on Theory of Computing (STOC’87), 123–131.CrossRefGoogle Scholar
Deutsch, D. (1985). Quantum theory, the church-turing principle, and the universal quantum computer. Proceedings Royal Society London, Series A. 400 97–117.Google Scholar
Deutsch, D. (1989). Quantum computational networks. Proceedings Royal Society London, Series A. 425 73–90.Google Scholar
Hainry, E., Péchoux, R. and Silva. (M.2023). A programming language characterizing quantum polynomial time. In: Proceedings of the 26th International Conference on Foundations of Software Science and Computation Structures (FoSSaCS 2023), Lecture Notes in Computer Science, vol. 13992. Springer, 156–175.Google Scholar
Holm, J., de Lichtenberg, K. and Thorup, M. (2001). Poly-logarithmic deterministic fully-dynamic algorithms for connectivity, minimum spanning tree, 2-edge, and biconnectivity. Journal of the ACM. 48 (4) 723–760.CrossRefGoogle Scholar
Kitaev, A. Y., Shen, A. H. and Vyalyi, M. N. (2002). Classical and Quantumn Computation (Graduate Studies in Mathematics), Americal Mathematical Society.Google Scholar
Kleene, S. C. (1936). General recursive functions of natural numbers. Mathematische Annalen. 112 (1) 727–742.CrossRefGoogle Scholar
Kleene, S. C. (1943). Recursive predicates and quantifiers. Transactions of the American Mathematical Society. 53 (1) 41–73.CrossRefGoogle Scholar
Munro, J. I. (1984). An implicit data structure for the dictionary problem that runs in polylogtime. In: Proceedings of the 25th Annual Symposium on Foundations of Computer Science (FOCS’84), 369–374.Google Scholar
Nielsen, M. A. and Chuang, I. L. (2016). Quantum Computation and Quantum Information, 10th Anniverswary edn., Cambridge University Press.Google Scholar
Nishimura, H. and Ozawa, M. (2002). Computational complexity of uniform quantum circuit families and quantum turing machines. Theoretical Computer Science. 276 (1-2) 147–181.CrossRefGoogle Scholar
Nishimura, H. and Yamakami, T. (2004). An Algorithmic argument for nonadaptive query complexity lower bounds on advised quantum computation (extended abstract). In: Proceedings of the 29th International Symposium on Mathematical Foundations of Computer Science (MFCS 2004), Lecture Notes in Computer Science, vol. 3153. Springer, 827–838. A complete version is available at arXiv:quant-ph/0312003.Google Scholar
Ozawa, M. and Nishimura, H. (2000). Local transition functions of quantum turing machines. RAIRO - Theoretical Informatics and Applications. 276 (5) 379–402.CrossRefGoogle Scholar
Raz, R. and Tal, A. (2022). Oracle separation of BQP and PH. Journal of the ACM. 69 (4) article 30.CrossRefGoogle Scholar
Soare, R. I. (1996). Computability and recursion. Bulletin of Symbolic Logic. 2 (3) 284–321.CrossRefGoogle Scholar
Tadaki, K., Yamakami, T. and Lin, J. C. H. (2010). Theory of one-tape linear-time Turing machines. Theoretical Computer Science. 411 (1) 22–43. An early extended abstract appeared in the Proceedings of the 30th SOFSEM Conference on Current Trends in Theory and Practice of Computer Science (SOFSEM 2004), Lecture Notes in Computer Science, vol.2932, pp.335-348, Springer, 2004.CrossRefGoogle Scholar
Vollmer, H. (1999). Introduction to Curcuit Complexity, Springer-Verlag.CrossRefGoogle Scholar
Yamakami, T. (1999). A foundation of programming a multi-tape quantum Turing machine. In: Proceedings of the 24th International Conference on Mathematical Foundations of Computer Science (MFCS’99), Lecture Notes in Computer Science, Springer, 430–441. Available also at arXiv:quant-ph/9906084.CrossRefGoogle Scholar
Yamakami, T. (2002). Quantum NP and a quantum hierarchy. In: Proceedings of the 2nd IFIP International Conference on Theoretical Computer Science (TCS 2002), Kluwer Academic Press (under the title of Foundations of Information Technology in the Era of Network and Mobile Computing), The International Federation for Information Processing, 323–336.CrossRefGoogle Scholar
Yamakami, T. (2003). Analysis of quantum functions. International Journal of Foundations of Computer Science. 14 (05) 815–852.CrossRefGoogle Scholar
Yamakami, T. (2020). A schematic definition of quantum polynomial time computability. The Journal of Symbolic Logic. 85 (4) 1546–1587. An early extended abstract appeared under a slightly different title in the Proceeidngs of the 9th Workshop on Non-Classical Models of Automata and Applications (NCMA 2017), Österreichische Computer Gesellschaft 2017, pp. 243-258, 2017.CrossRefGoogle Scholar
Yamakami, T. (2022a). Nonuniform families of polynomial-size quantum finite automata and quantum logarithmic-space computation with polynomial-size advice. Information and Computation. 286, article 104783. A preliminary version appeared in the Proceedings of the 20th International Conference on Descriptional Complexity of Formal Systems (DCFS 2018), Lecture Notes in Computer Sceince, vol. 10952, pp. 237–249, Springer, 2018.CrossRefGoogle Scholar
Yamakami, T. (2022b). Expressing power of elementary quantum recursion schemes for quantum logarithmic-time computability. In: Proceedings of the 28th International Conference on Logic, Language, Information, and Computation (WoLLIC 2022), Lecture Notes in Computer Science, vol. 13468, pp. 88–104, Springer, 2022.Google Scholar
Yamakami, T. and Yao, A. C. (1999). NQPC=co-C=P., Information Processing Letters. 71 63–69.CrossRefGoogle Scholar
Yao, A. C. (1993). Quantum circuit complexity. In: Proceedings of the 34th Annual IEEE Symposium on Foundations of Computer Science (FOCS’93), 80–91.Google Scholar