Hostname: page-component-669899f699-chc8l Total loading time: 0 Render date: 2025-04-30T21:15:35.959Z Has data issue: false hasContentIssue false
  • English
  • Français

The Ulam–Hammersley problem for multiset permutations

Part of: Special processes Limit theorems

Published online by Cambridge University Press:  09 May 2024

LUCAS GERIN
LUCAS GERIN*
Affiliation:
CMAP, CNRS, École Polytechnique, 91120 Palaiseau, France. e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We obtain the asymptotic behaviour of the longest increasing/non-decreasing subsequences in a random uniform multiset permutation in which each element in $\{1,\dots,n\}$ occurs k times, where k may depend on n. This generalises the famous Ulam–Hammersley problem of the case 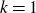$k=1$. The proof relies on poissonisation and on a careful non-asymptotic analysis of variants of the Hammersley–Aldous–Diaconis particle system.

MSC classification

Primary: 60K35: Interacting random processes; statistical mechanics type models; percolation theory
Secondary: 60F15: Strong theorems
Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 177 , Issue 1 , July 2024 , pp. 23 - 48
Copyright
© The Author(s), 2024. Published by Cambridge University Press on behalf of Cambridge Philosophical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Aldous, D. and Diaconis, P.. Hammersley’s interacting particle process and longest increasing subsequences. Probab. Theory Related Fields 103(2) (1995), 199–213.CrossRefGoogle Scholar
Baik, J., Deift, P. and Johansson, K.. On the distribution of the length of the longest increasing subsequence of random permutations. J. Amer. Math. Soc. 12(4) (1999), 1119–1178.CrossRefGoogle Scholar
Basdevant, A-L., Enriquez, N. Gerin, L. and Gouéré, J-B.. Discrete Hammersley’s lines with sources and sinks. ALEA Lat. Am. J. Probab. Math. Stat. 13 (2016), 33–52.Google Scholar
Biane, P.. Approximate factorization and concentration for characters of symmetric groups. Internat. Math. Res. Notices (2) (2001), 179–192.CrossRefGoogle Scholar
Boyer, A.. Chapter 3 (in English) of Stationnarité bidimensionnelle de modèles aléatoires du plan. PhD. thesis. Université Paris-Saclay, (2022), Available at https://tel.archives-ouvertes.fr/tel-03783603/.Google Scholar
Clifton, A., Deb, B. Huang, Y., Spiro, S. and Yoo, S.. Continuously increasing subsequences of random multiset permutations. Sém. Lothar. Combin. 86B(Art. 4, 11) (2022). (Proceedings of FPSAC’22.)Google Scholar
Cator, E. and Groeneboom, P.. Hammersley’s process with sources and sinks. Ann. Probab. 33(3) (2005), 879–903.Google Scholar
Cator, E. and Groeneboom, P.. Second class particles and cube root asymptotics for Hammersley’s process. Ann. Probab. 34(4) (2006), 1273–1295.CrossRefGoogle Scholar
Ciech, F. and Georgiou, N.. Order of the variance in the discrete Hammersley process with boundaries. J. Statist. Phys. 176(3) (2019), 501–638.Google Scholar
Cormen, T. H., Leiserson, C. E., Rivest, R. L. and Stein, C.. Introduction to Algorithms (MIT Press, Cambridge, MA, third edition, 2009).Google Scholar
Ferrari, P. A.. Limit theorems for tagged particles. Markov Process. Related Fields 2(1) (1996), 17–40.Google Scholar
Ferrari, P. A. and Martin, J. B.. Multi-class processes, dual points and $M/M/1$ queues. Markov Process. Related Fields 12(2) (2006), 175–201.Google Scholar
Hammersley, J. M.. A few seedlings of research. In Proceedings of the 6th Berkeley Symp. Math. Statist. and Probability, vol. 1 (1972), 345–394.Google Scholar
Janson, S., Łuczak, T. and Rucinski, A.. Random Graphs. Wiley-Interscience Series in Discrete Mathematics and Optimization (Wiley-Interscience, New York, 2000).CrossRefGoogle Scholar
Romik, D.. The surprising mathematics of longest increasing subsequences. Institute of Mathematical Statistics Textbooks, vol. 4 (Cambridge University Press, New York, 2015).CrossRefGoogle Scholar
Seppäläinen, T.. Increasing sequences of independent points on the planar lattice. Ann. Appl. Probab. 7(4) (1997), 886–898.CrossRefGoogle Scholar
Seppäläinen, T.. Exact limiting shape for a simplified model of first-passage percolation on the plane. Ann. Probab. 26(3) (1998), 1232–1250.CrossRefGoogle Scholar
Steele, J. M.. Probability theory and combinatorial optimization. Society for Industrial and Applied Mathematics (SIAM), 69 1997.Google Scholar
Veršik, A. M. and Kerov, S. V.. Asymptotics of Plancherel measure of symmetrical group and limit form of Young tables. Dokl. Akad. Nauk SSSR 233(6) (1977), 1024–1027.Google Scholar
Wainwright, M. J.. High-dimensional statistics. Cambridge Series in Statistical and Probabilistic Mathematic, vol. 48 (Cambridge University Press, Cambridge, 2019).Google Scholar