Hostname: page-component-669899f699-chc8l Total loading time: 0 Render date: 2025-05-05T05:48:39.831Z Has data issue: false hasContentIssue false
  • English
  • Français

Most integers are not a sum of two palindromes

Part of: Elementary number theory Sequences and sets

Published online by Cambridge University Press:  22 October 2024

DMITRII ZAKHAROV
DMITRII ZAKHAROV*
Affiliation:
Department of Mathematics, Massachusetts Institute of Technology, 77 Massachsetts Ave, Cambridge, MA 02139, U.S.A. e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

For 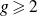$g \geqslant 2$, we show that the number of positive integers at most X which can be written as sum of two base g palindromes is at most 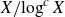${X}/{\log^c X}$. This answers a question of Baxter, Cilleruelo and Luca.

MSC classification

Primary: 11B13: Additive bases, including sumsets 11A63: Radix representation; digital problems
Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 177 , Issue 2 , September 2024 , pp. 363 - 366
Copyright
© The Author(s), 2024. Published by Cambridge University Press on behalf of Cambridge Philosophical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

Footnotes

†

This research was supported by the Jane Street Graduate Fellowship.

References

Alon, N. and Spencer, J.H.. The Probabilistic Method (John Wiley & Sons, 2016).Google Scholar
Banks, W. D.. Every natural number is the sum of forty-nine palindromes. Integers. 16(A3, 9) (2016) i.e (2016).Google Scholar
Cilleruelo, J., Luca, and Baxter, L.. Every positive integer is a sum of three palindromes. Math. Comp. 87 (2018), 3023–3055.CrossRefGoogle Scholar
Rajasekaran, A., Shallit, J. and Smith, T.. Sums of palindromes: an approach via automata, (35th Symposium on Theoretical Aspects of Computer Science, 2018).Google Scholar
Rajasekaran, A., Shallit, J. and Smith, T.. Additive number theory via automata theory. Theory Comput. Syst. 64 (2020), 542–567.CrossRefGoogle Scholar