Hostname: page-component-669899f699-b58lm Total loading time: 0 Render date: 2025-04-30T20:57:53.480Z Has data issue: false hasContentIssue false
  • English
  • Français

Multiplicative dependence of rational values modulo approximate finitely generated groups

Part of: Algebraic number theory: global fields Multiplicative number theory

Published online by Cambridge University Press:  19 September 2024

ATTILA BÉRCZES ,
YANN BUGEAUD ,
KÁLMÁN GYŐRY ,
JORGE MELLO ,
ALINA OSTAFE  and
MIN SHA
ATTILA BÉRCZES
Affiliation:
Institute of Mathematics, University of Debrecen, H-4010 Debrecen, P.O. BOX 12, Hungary e-mail: [email protected]
YANN BUGEAUD
Affiliation:
Institut de Recherche Mathématique Avancée, U.M.R. 7501, Université de Strasbourg et C.N.R.S., 7, rue René Descartes, 67084 Strasbourg, France; Institut Universitaire de France e-mail: [email protected]
KÁLMÁN GYŐRY
Affiliation:
Institute of Mathematics, University of Debrecen, H-4010 Debrecen, P.O. Box 12, Hungary e-mail: [email protected]
JORGE MELLO
Affiliation:
Department of Mathematics and Statistics, Oakland University, 48307 Michigan, United States e-mail: [email protected]
ALINA OSTAFE
Affiliation:
School of Mathematics and Statistics, University of New South Wales, Sydney, NSW 2052, Australia e-mail: [email protected]
MIN SHA
Affiliation:
School of Mathematical Sciences, South China Normal University, Guangzhou 510631, China e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper, we establish some finiteness results about the multiplicative dependence of rational values modulo sets which are ‘close’ (with respect to the Weil height) to division groups of finitely generated multiplicative groups of a number field K. For example, we show that under some conditions on rational functions 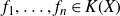$f_1, \ldots, f_n\in K(X)$, there are only finitely many elements 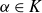$\alpha \in K$ such that $f_1(\alpha),\ldots,f_n(\alpha)$ are multiplicatively dependent modulo such sets.

MSC classification

Primary: 11N25: Distribution of integers with specified multiplicative constraints
Secondary: 11R04: Algebraic numbers; rings of algebraic integers
Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 177 , Issue 1 , July 2024 , pp. 149 - 165
Copyright
© The Author(s), 2024. Published by Cambridge University Press on behalf of Cambridge Philosophical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Aliev, I. and Smyth, C. J.. Solving algebraic equations in roots of unity. Forum Math. 24 (2012), 641–665.CrossRefGoogle Scholar
Amoroso, F.. On a conjecture of G. Rémond. Ann. Scuola Norm. Sup. Pise Cl. Sci. 15 (2016), 599–608.Google Scholar
Amoroso, F. and Viada, E.. Small points on subvarieties of a torus. Duke Math. J. 150 (2009), 407–442.CrossRefGoogle Scholar
Barroero, F., Capuano, L., Mérai, L., Ostafe, A. and Sha, M.. Multiplicative and linear dependence in finite fields and on elliptic curves modulo primes. Int. Math. Res. Not. 2022 (2022), 16094–16137.CrossRefGoogle Scholar
Barroero, F. and Sha, M.. Torsion points with multiplicatively dependent coordinates on elliptic curves. Bull. London Math. Soc. 52 (2020), 807–815.CrossRefGoogle Scholar
Bérczes, A., Bugeaud, Y., Győry, K., Mello, J., Ostafe, A. and Sha, M.. Explicit bounds for the solutions of superelliptic equations over number fields. Forum Math. 2024, https://doi.org/10.1515/forum-2023-0381.CrossRefGoogle Scholar
Bérczes, A., Evertse, J.-H. and Győry, K.. Effective results for hyper- and superelliptic equations over number fields. Publ. Math. Debrecen 82 (2013), 727–756.CrossRefGoogle Scholar
Bérczes, A., Evertse, J.-H., Győry, K. and Pontreau, C.. Effective results for points on certain subvarieties of tori. Math. Proc. Camb. Phil. Soc. 147 (2009), 69–94.CrossRefGoogle Scholar
Bérczes, A., Ostafe, A., Shparlinski, I. E. and Silverman, J. H.. Multiplicative dependence among iterated values of rational functions modulo finitely generated groups. Int. Math. Res. Not. 2021 (2021), 9045–9082.CrossRefGoogle Scholar
Beukers, F. and Smyth, C. J.. Cyclotomic points on curves. Number Theory for the Millenium (Urbana, Illinois, 2000), I (A. K. Peters, 2002), 67–85.Google Scholar
Bombieri, E., Habegger, P., Masser, D. and Zannier, U.. A note on Maurin’s theorem. Rend. Lincei Mat. Appl. 21 (2010), 251–260.Google Scholar
Bombieri, E., Masser, D. and Zannier, U.. Intersecting a curve with algebraic subgroups of multiplicative groups. Int. Math. Res. Not. 1999 (1999), 1119–1140.CrossRefGoogle Scholar
Bombieri, E. and Zannier, U.. Algebraic points on subvarieties of ${\mathbb{G}_{\textrm{m}}}^n$ . Int. Math. Res. Not. 1995 (1995), 333–347.CrossRefGoogle Scholar
Dubickas, A. and Sha, M.. Multiplicative dependence of the translations of algebraic numbers. Rev. Mat. Iberoam. 34 (2018), 1789–1808.CrossRefGoogle Scholar
Dvornicich, R. and Zannier, U.. Cyclotomic diophantine problems (Hilbert irreducibility and invariant sets for polynomial maps). Duke Math. J. 139 (2007), 527–554.CrossRefGoogle Scholar
Evertse, J.-H.. Points on subvarieties of tori. A panorama of number theory or the view from Baker’s garden (Zürich, 1999) (Cambridge University Press, 2002), 214–230.Google Scholar
Faltings, G.. Endlichkeitssätze fur abelsche Varietäten über Zahlkorpern. Invent. Math. 73 (1983), 349–366.CrossRefGoogle Scholar
Gao, S.. Elements of provable high order in finite fields. Proc. Amer. Math. Soc. 127 (1999), 1615–1623.Google Scholar
Konyagin, S. V., Sha, M., Shparlinski, I. E. and Stewart, C. L.. On the distribution of multiplicatively dependent vectors. Math. Res. Lett. 30 (2023), 509–540.CrossRefGoogle Scholar
Laurent, M.. Equations diophantiennes exponentielles. Invent. Math. 78 (1984), 299–327.CrossRefGoogle Scholar
Liardet, P.. Sur une conjecture de Serge Lang. Astérisque 24-25 (1975), 187–210.Google Scholar
Loxton, J. H. and van der Poorten, A. J.. Multiplicative dependence in number fields. Acta Arith. 42 (1983), 291–302.CrossRefGoogle Scholar
Martinez, C.. The number of maximal torsion cosets on subvarieties of tori. J. Reine Angew. Math. 755 (2019), 10–126.Google Scholar
Maurin, G.. Courbes algébriques et équations multiplicatives. Math. Ann. 341 (2008), 789–824.CrossRefGoogle Scholar
Maurin, G.. Équations multiplicatives sur les sous-variétés des tores. Int. Math. Res. Not. 2011 (2011), 5259–5366.Google Scholar
Mazur, B.. Abelian varieties and the Mordell–Lang conjecture. Model theory, algebra, and geometry. Math. Sci. Res. Inst. Publ. 39 (Cambridge University Press, 2000), 199–227.Google Scholar
Ostafe, A., Sha, M., Shparlinski, I. E. and Zannier, U.. On abelian multiplicatively dependent points on a curve in a torus. Q. J. Math. 69 (2018), 391–401.CrossRefGoogle Scholar
Ostafe, A., Sha, M., Shparlinski, I. E. and Zannier, U.. On multiplicative dependence of values of rational functions and a generalisation of the Northcott theorem. Michigan Math. J. 68 (2019), 385–407.CrossRefGoogle Scholar
Ostafe, A. and Shparlinski, I. E.. Orbits of algebraic dynamical systems in subgroups and subfields. Number Theory - Diophantine problems, uniform distribution and applications, Elsholtz, C. and Grabner, P. (Eds.) (Springer, 2017), 347–368.CrossRefGoogle Scholar
Ostafe, A. and Shparlinski, I. E.. On the Skolem problem and some related questions for parametric families of linear recurrence sequences. Canad. J. Math. 74 (2022), 773–792.CrossRefGoogle Scholar
Pappalardi, F., Sha, M., Shparlinski, I. E. and Stewart, C. L.. On multiplicatively dependent vectors of algebraic numbers. Trans. Amer. Math. Soc. 370 (2018), 6221–6244.CrossRefGoogle Scholar
Pontreau, C.. A Mordell–Lang plus Bogolomov type result for curves in ${\mathbb{G}_{\textrm{m}}}^2$ . Monatsh. Math. 157 (2009), 267–281.CrossRefGoogle Scholar
Poonen, B.. Mordell–Lang plus Bogomolov. Invent. Math. 137 (1999), 413–425.CrossRefGoogle Scholar
Pottmeyer, L.. Fields generated by finite rank subgroups of $\overline{{\mathbb{Q}}}^*$ . Int. J. Number Theory 17 (2021), 1079–1089.CrossRefGoogle Scholar
van der Poorten, A. J. and Loxton, J. H.. Multiplicative relations in number fields. Bull. Austral. Math. Soc. 16 (1977), 83–98.CrossRefGoogle Scholar
Rémond, G.. Sur les sous-variétés des tores. Compositio. Math. 134 (2002), 337–366.CrossRefGoogle Scholar
Rémond, G.. Généralisations du problème de Lehmer et applications à la conjecture de Zilber–Pink. Panor. Synth. 52 (2017), 243–284.Google Scholar
Schinzel, A. and Tijdeman, R.. On the equation $y^m = P(x)$ . Acta Arith. 31 (1976), 199–204.CrossRefGoogle Scholar
Schmidt, W. M.. Heights of points on subvarieties of ${\mathbb{G}_{\textrm{m}}}^n$ . Number Theory (Paris, 1993–1994). London Math. Soc. Lecture Note Ser. 235 (Cambridge University Press, 1996), 157–187.CrossRefGoogle Scholar
Shorey, T. N. and Tijdeman, R.. Exponential Diophantine Equations. (Cambridge University Press, Cambridge, 1986).CrossRefGoogle Scholar
Stewart, C. L.. On heights of multiplicatively dependent algebraic numbers. Acta Arith. 133 (2008), 97–108.CrossRefGoogle Scholar
Young, M.. On multiplicative independence of rational function iterates. Monatsh. Math. 192 (2020), 225–247.CrossRefGoogle Scholar