Hostname: page-component-669899f699-7tmb6 Total loading time: 0 Render date: 2025-04-29T10:05:03.490Z Has data issue: false hasContentIssue false
  • English
  • Français

Recursive averages and the renewal theorem

Published online by Cambridge University Press:  12 November 2024

G. J. O. Jameson
G. J. O. Jameson*
Affiliation:
13 Sandown Road, Lancaster LA1 4LN e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Extract

Consider the sequence of numbers an defined by the iteration (1)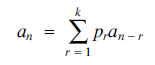 for n ≥ k, where pr 1 ≤ r ≤ k) are non-negative numbers with 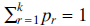and the starting values are given. So an is a weighted average of the previous k terms.

Type
Articles
Information
The Mathematical Gazette , Volume 108 , Issue 573 , November 2024 , pp. 437 - 449
Check for updates
Copyright
© The Authors, 2024 Published by Cambridge University Press on behalf of The Mathematical Association

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Flanders, H., Averaging sequences again, Math. Gaz. 80 (July 1996) pp. 219-222.CrossRefGoogle Scholar
Lord, N., Sequences of averages revisited, Math. Gaz. 95 (July 2011) pp. 314-317.CrossRefGoogle Scholar
Rohan Manojkumar Shenoy, The discrete renwal theorem with bounded inter-event times, Math. Gaz. 107 (July 2023) pp. 343-348.CrossRefGoogle Scholar
Sanders, P., Averaging sequences, Math. Gaz. 78 (November 1994) pp. 326-328.CrossRefGoogle Scholar
Feller, W., An introduction to probability theory and its applications, Wiley (1971).Google Scholar
Lotka, A. J., A contribution to the theory of self-renewing aggregates, with special reference to industrial replacement, Ann. Math. Stats. 10 (1939) pp. 1–25.CrossRefGoogle Scholar
Keyfitz, N., Introduction to the mathematics of population, Addison-Wesley (1968).Google Scholar
Apostol, T. M., Mathematical analysis, Addison-Wesley (1957).Google Scholar
Bachman, G. and Narici, L., Functional analysis, Academic Press (1966). Google Scholar