Hostname: page-component-669899f699-b58lm Total loading time: 0 Render date: 2025-04-29T11:20:26.892Z Has data issue: false hasContentIssue false
  • English
  • Français

RIGIDITY FOR VON NEUMANN ALGEBRAS OF GRAPH PRODUCT GROUPS II. SUPERRIGIDITY RESULTS

Part of: Selfadjoint operator algebras

Published online by Cambridge University Press:  25 November 2024

Ionuţ Chifan ,
Michael Davis  and
Daniel Drimbe Open the ORCID record for Daniel Drimbe [Opens in a new window]
Ionuţ Chifan
Affiliation:
14 MacLean Hall, Department of Mathematics, The University of Iowa, IA, 52242, USA [email protected]
Michael Davis
Affiliation:
14 MacLean Hall, Department of Mathematics, The University of Iowa, IA, 52242, USA [email protected]
Daniel Drimbe*
Affiliation:
Mathematical Institute, University of Oxford, Woodstock Road, Oxford OX2 6GG, UK 14 MacLean Hall, Department of Mathematics, The University of Iowa, IA, 52242
*
[email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

In [CDD22], we investigated the structure of $\ast $-isomorphisms between von Neumann algebras 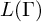$L(\Gamma )$ associated with graph product groups $\Gamma $ of flower-shaped graphs and property (T) wreath-like product vertex groups, as in [CIOS21]. In this follow-up, we continue the structural study of these algebras by establishing that these graph product groups $\Gamma $ are entirely recognizable from the category of all von Neumann algebras arising from an arbitrary nontrivial graph product group with infinite vertex groups. A sharper $C^*$-algebraic version of this statement is also obtained. In the process of proving these results, we also extend the main 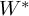$W^*$-superrigidity result from [CIOS21] to direct products of property (T) wreath-like product groups.

Keywords

von Neumann algebrasgraph product of groupsproduct rigiditysuperrigidity

MSC classification

Primary: 46L10: General theory of von Neumann algebras
Secondary: 46L36: Classification of factors
Type
Research Article
Information
Journal of the Institute of Mathematics of Jussieu , Volume 24 , Issue 1 , January 2025 , pp. 117 - 156
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Agol, I., The virtual Haken conjecture, Doc. Math. 18 (2013), 1045–1087. With an appendix by I. Agol, D. Groves, J. Manning.CrossRefGoogle Scholar
Antolín, Y. and Minasyan, A., Tits alternatives for graph products, J. Reine Angew. Math. 704 (2015), 55–83.CrossRefGoogle Scholar
Berbec, M., W ${}^{\ast }$ -superrigidity for wreath products with groups having positive first ${\ell}^2$ -Betti number, Int. J. Math. 26(1) (2015), 1550003, 27.CrossRefGoogle Scholar
Berbec, M. and Vaes, S., ${\mathrm{W}}^{\ast }$ -superrigidity for group von Neumann algebras of left-right wreath products, Proc. Lond. Math. Soc. 108(5) (2014), 1116–1152.CrossRefGoogle Scholar
Breuillard, E., Kalantar, M., Kennedy, M. and Ozawa, N., ${\mathrm{C}}^{\ast }$ -simplicity and the unique trace property for discrete groups, Publ. Math. Inst. Hautes Études Sci. 126 (2017), 35–71.CrossRefGoogle Scholar
Brown, N. P. and Ozawa, N., ${\mathrm{C}}^{\ast }$ -algebras and finite-dimensional approximations, in Graduate Studies in Mathematics, 88, pp. xi–509 (American Mathematical Society, Providence, RI, 2008).Google Scholar
Caspers, M., Absence of Cartan subalgebras for right-angled Hecke von Neumann algebras, Anal. PDE 13(1) (2020), 1–28.CrossRefGoogle Scholar
Caspers, M. and Fima, P., Graph products of operator algebras, J. Noncommut. Geom. 11(1) (2017), 367–411.CrossRefGoogle Scholar
Chifan, I., Das, S., Houdayer, C. and Khan, K., Examples of property (T) factors with trivial fundamental group, to appear in Amer. J. Math., https://arxiv.org/abs/2003.08857.Google Scholar
Chifan, I., Davis, M. and Drimbe, D., Rigidity for von Neumann algebras of graph product groups. I. Structure of automorphisms, Preprint, 2022, https://arxiv.org/html/2209.12996v2.Google Scholar
Chifan, I., de Santiago, R. and Sinclair, T., ${\mathrm{W}}^{\ast}$ -rigidity for the von Neumann algebras of products of hyperbolic groups, Geom. Funct. Anal. 26(1) (2016), 136–159.CrossRefGoogle Scholar
Chifan, I., de Santiago, R. and Sucpikarnon, W., Tensor product decompositions of II ${}_1$ factors arising from extensions of amalgamated free product groups, Comm. Math. Phys. 364 (2018), 1163–1194.CrossRefGoogle Scholar
Chifan, I., Diaz-Arias, A. and Drimbe, D., New examples of ${\mathrm{W}}^{\ast }$ and ${\mathrm{C}}^{\ast }$ -superrigid groups, Adv. Math. 412 (2023), Paper no. 108797.CrossRefGoogle Scholar
Chifan, I., Diaz-Arias, A. and Drimbe, D., ${\mathrm{W}}^{\ast}$ and ${\mathrm{C}}^{\ast}$ -superrigidity results for coinduced groups, J. Funct. Anal. 284(1) (2023), 109730.CrossRefGoogle Scholar
Chifan, I. and Houdayer, C., Bass-Serre rigidity results in von Neumann algebras, Duke Math. J. 153(1) (2010), 23–54.CrossRefGoogle Scholar
Chifan, I. and Ioana, A., Amalgamated free product rigidity for group von Neumann algebras, Adv. Math. 329 (2018), 819–850.CrossRefGoogle Scholar
Chifan, I., Ioana, A. and Kida, Y., ${\mathrm{W}}^{\ast }$ -superrigidity for arbitrary actions of central quotients of braid groups, Math. Ann. 361 (2015), 563–582.CrossRefGoogle Scholar
Chifan, I., Ioana, A., Osin, D. and Sun, B., Wreath-like product groups and rigidity of their von Neumann algebras, Ann. of Math. 198(3) (2023), 1261–1303.CrossRefGoogle Scholar
Chifan, I., Ioana, A., Osin, D. and Sun, B., Uncountable families of ${\mathrm{W}}^{\ast}$ and ${\mathrm{C}}^{\ast}$ -superrigid Kazhdan groups, Preprint 2023.Google Scholar
Chifan, I., Kida, Y. and Pant, S., Primeness results for von Neumann algebras associated with surface braid groups, Int. Math. Res. Not. IMRN 2016(16) (2016), 4807–4848.CrossRefGoogle Scholar
Chifan, I. and Kunnawalkam-Elyavalli, S., Cartan subalgebras in von Neumann algebras associated with graph product groups, Groups Geom. Dyn. 18(2) (2024), 749–759.CrossRefGoogle Scholar
Connes, A., Classification of injective factors. Cases II ${}_1$ , II ${}_{\infty }$ , III ${}_{\unicode{x3bb}}$ , $\unicode{x3bb} \ne 1,$ Ann. of Math. (2) 104(1) (1976), 73–115.CrossRefGoogle Scholar
Connes, A., Classification des facteurs. Operator algebras and applications, part $2$ , (Kingston, Ont., 1980), in Proceedings of Symposia in Pure Mathematics, 38, pp. 43–109 (American Mathematical Society, Providence, R.I., 1982).Google Scholar
Chifan, I. and Udrea, B., Some rigidity results for II ${}_1$ factors arising from wreath products of property (T) groups, J. Funct. Anal. 278(7) (2020), 108419.CrossRefGoogle Scholar
Drimbe, D., Hoff, D. and Ioana, A., Prime II ${}_1$ factors arising from irreducible lattices in products of rank one simple Lie groups, J. Reine Angew. Math. 757 (2019), 197–246.CrossRefGoogle Scholar
Ding, C. and Kunnawalkam Elayavalli, S., Proper proximality for groups acting on trees, Preprint, 2021, https://www.researchgate.net/publication/353066965_Proper_proximality_for_groups_acting_on_trees.Google Scholar
D. Drimbe, Prime II ${}_1$ factors arising from actions of product groups, J. Funct. Anal. 278(5) (2020), 108366, 23.Google Scholar
Drimbe, D., Orbit equivalence rigidity for product actions, Comm. Math. Phys. 379(1) (2020), 41–59.CrossRefGoogle Scholar
Drimbe, D., Product rigidity in von Neumann and C ${}^{\ast }$ -algebras via s-malleable deformations, Comm. Math. Phys. 388(1) (2021), 329–349.CrossRefGoogle Scholar
Fang, J., Gao, S. and Smith, R., The relative weak asymptotic homomorphism property for inclusions of finite von Neumann algebras, Int. J. Math. 22(7) (2011), 991–1011.CrossRefGoogle Scholar
Ge, L., On maximal injective subalgebras of factors, Adv. Math. 118(1) (1996), 34–70.CrossRefGoogle Scholar
Green, E., Graph Products of Groups, PhD Thesis, The University of Leeds, 1990, http://etheses.whiterose.ac.uk/236/.Google Scholar
Genevois, A. and Martin, A., Automorphisms of graph products of groups from a geometric perspective, Proc. Lond. Math. Soc. (3) 119(6) (2019), 1745–1779.CrossRefGoogle Scholar
Haglund, F. and Wise, D., Special cube complexes, Geom. Funct. Anal. 17(5) (2008), 1551–1620.CrossRefGoogle Scholar
Horbez, C. and Huang, J., Measure equivalence classification of transvection-free right-angled Artin groups, J. Éc. Polytech. Math. 9 (2022), 1021–1067.CrossRefGoogle Scholar
Horbez, C. and Huang, J., Orbit equivalence rigidity of irreducible actions of right-angled Artin groups, Preprint 2021, https://arxiv.org/abs/2110.04141.Google Scholar
Ioana, A., Peterson, J. and Popa, S., Amalgamated free products of weakly rigid factors and calculation of their symmetry groups, Acta Math. 200(1) (2008), 85–153.CrossRefGoogle Scholar
Ioana, A., ${\mathrm{W}}^{\ast }$ -superrigidity for Bernoulli actions of property (T) groups, J. Amer. Math. Soc. 24(4) (2011), 1175–1226.CrossRefGoogle Scholar
Ioana, A., Uniqueness of the group measure space decomposition for Popa’s factors, Geom. Funct. Anal. 22(3) (2012), 699–732.CrossRefGoogle Scholar
Ioana, A., Classification and rigidity for von Neumann algebras, ECM, EMS (2013), 601–625.CrossRefGoogle Scholar
Ioana, A., Cartan subalgebras of amalgamated free product II ${}_1$ factors, Ann. Sci. Éc. Norm. Supér. (4) 48(1) (2015), 71–130. With an appendix by Ioana, Adrian and Vaes, Stefaan.CrossRefGoogle Scholar
Ioana, A., Rigidity for von Neumann algebras, in Proceedings of the International Congress of Mathematicians-Rio de Janeiro 2018. Invited Lectures, vol. III, pp. 1639–1672 (World Scientific Publishing, Hackensack, NJ, 2018).Google Scholar
Ioana, A., Popa, S. and Vaes, S., A class of superrigid group von Neumann algebras, Ann. of Math. (2) 178(1) (2013), 231–286.CrossRefGoogle Scholar
Jones, V. F. R., Index for subfactors, Invent. Math. 72(1) (1983), 1–25.CrossRefGoogle Scholar
Jones, V. F. R., Ten problems, in Mathematics: Frontiers and perspectives (ed. by Arnold, V., Atiyah, M., Lax, P. and Mazur, B.), pp. 79–91 (American Mathematical Society, Providence, RI, 2000).Google Scholar
Krogager, A. S. and Vaes, S., A class of $\mathrm{I}{\mathrm{I}}_1$ factors with exactly two group measure space decompositions, J. Math. Pures Appl. (9) 108(1) (2017), 88–110.CrossRefGoogle Scholar
Minasyan, A. and Osin, D., Acylindrical hyperbolicity of groups acting on trees, Math. Ann. 362(3–4) (2015), 1055–1105.CrossRefGoogle Scholar
Murray, F. J. and von Neumann, J., On rings of operators IV, Ann. of Math. (2) 44 (1943), 716–808.CrossRefGoogle Scholar
Mineyev, I. and Yu, G., The Baum-Connes conjecture for hyperbolic groups, Invent. Math. 149(1) (2002), 97–122.CrossRefGoogle Scholar
Oyono-Oyono, H., La conjecture de Baum-Connes pour les groupes agissant sur les arbres. C. R. Acad. Sci. Paris Sér. I Math. 326(7) (1998), 799–804.CrossRefGoogle Scholar
Oyono-Oyono, H., Baum-Connes conjecture and extensions, J. Reine Angew. Math. 532 (2001), 133–149.Google Scholar
Ozawa, N. and Popa, S., Some prime factorization results for type II ${}_1$ factors, Invent. Math. 156(2) (2004), 223–234.CrossRefGoogle Scholar
Ozawa, N. and Popa, S., On a class of II ${}_1$ factors with at most one Cartan subalgebra, Ann. of Math. (2) 172(1) (2010), 713–749.CrossRefGoogle Scholar
Popa, S., Some properties of the symmetric enveloping algebra of a factor, with applications to amenability and property (T), Doc. Math. 4 (1999), 665–744.CrossRefGoogle Scholar
Popa, S., On a class of type II ${}_1$ factors with Betti numbers invariants, Ann. of Math. (2) 163 (2006), 809–899.CrossRefGoogle Scholar
Popa, S., Strong rigidity of II ${}_1$ factors arising from malleable actions of $\mathrm{w}$ -rigid groups I, Invent. Math. 165(2) (2006), 369–408.CrossRefGoogle Scholar
Popa, S., Strong rigidity of II ${}_1$ factors arising from malleable actions of $\mathrm{w}$ -rigid groups II, Invent. Math. 165(2) (2006), 409–452.CrossRefGoogle Scholar
Popa, S., Deformation and rigidity for group actions and von Neumann algebras, in International Congress of Mathematicians, vol. I, pp. 445–477 (European Mathematical Society, Zürich, 2007).Google Scholar
Pimsner, M. and Popa, S., Entropy and index for subfactors, Ann. Sci. Éc. Norm. Supér. 19 (1986), 57–106.CrossRefGoogle Scholar
Popa, S. and Vaes, S., Group measure space decomposition of II ${}_1$ factors and W ${}^{\ast }$ –superrigidity, Invent. Math. 182(2) (2010), 371–417.CrossRefGoogle Scholar
Popa, S. and Vaes, S., Unique Cartan decomposition for $\mathrm{I}{\mathrm{I}}_1$ factors arising from arbitrary actions of free groups, Acta Math. 212(1) (2014), 141–198.CrossRefGoogle Scholar
Popa, S. and Vaes, S., Unique Cartan decomposition for $\mathrm{I}{\mathrm{I}}_1$ factors arising from arbitrary actions of hyperbolic groups, J. Reine Angew. Math. 694 (2014), 215–239.CrossRefGoogle Scholar
Sinclair, A. and Smith, R., Finite von Neumann algebras and MASAs, in London Mathematical Society Lecture Note Series, 351, pp. i–400 (Cambridge University Press, Cambridge, 2008).Google Scholar
Vaes, S., Rigidity results for Bernoulli actions and their von Neumann algebras (after Sorin Popa), Séminaire Bourbaki, vol. 2005/2006. Astérisque 311(961) (2007), viii, 237–294.Google Scholar
Vaes, S., Explicit computations of all finite index bimodules for a family of II ${}_1$ factors, Ann. Sci. Éc. Norm. Supér. (4) 41(5) (2008), 743–788.CrossRefGoogle Scholar
Vaes, S., One-cohomology and the uniqueness of the group measure space decomposition of a II ${}_1$ factor, Math. Ann. 355(2) (2013), 661–696.CrossRefGoogle Scholar
Vaes, S., Rigidity for von Neumann algebras and their invariants, Proceedings of the International Congress of Mathematicians. vol. III, pp. 1624–1650 (Hindustan Book Agency, New Delhi, 2010).Google Scholar
Wise, D. T., Research announcement: The structure of groups with a quasiconvex hierarchy, Electron. Res. Announc. Math. Sci. 16 (2009), 44–55.Google Scholar