Hostname: page-component-669899f699-8p65j Total loading time: 0 Render date: 2025-05-03T21:15:46.690Z Has data issue: false hasContentIssue false
  • English
  • Français

RANDOM REAL BRANCHED COVERINGS OF THE PROJECTIVE LINE

Part of: Limit theorems Curves Holomorphic functions of several complex variables

Published online by Cambridge University Press:  09 February 2021

Michele Ancona Open the ORCID record for Michele Ancona [Opens in a new window]
Michele Ancona*
Affiliation:
Tel Aviv University, School of Mathematical Sciences ([email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper, we construct a natural probability measure on the space of real branched coverings from a real projective algebraic curve 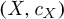$(X,c_X)$ to the projective line 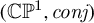$(\mathbb{C} \mathbb {P}^1,\textit{conj} )$ . We prove that the space of degree d real branched coverings having “many” real branched points (for example, more than 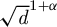$\sqrt {d}^{1+\alpha }$ , for any 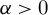$\alpha>0$ ) has exponentially small measure. In particular, maximal real branched coverings – that is, real branched coverings such that all the branched points are real – are exponentially rare.

Keywords

real algebraic curvesbranched coveringsrandom mapsBergman kernel

MSC classification

Primary: 14P99: None of the above, but in this section
Secondary: 14H30: Coverings, fundamental group 60F10: Large deviations 32A25: Integral representations; canonical kernels (Szegő, Bergman, etc.)
Type
Research Article
Information
Journal of the Institute of Mathematics of Jussieu , Volume 21 , Issue 5 , September 2022 , pp. 1783 - 1799
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

Footnotes

The author is supported by the Israeli Science Foundation through ISF Grants 382/15 and 501/18

References

Ancona, M., Expected number and distribution of critical points of real Lefschetz pencils, Ann. Inst. Fourier (Grenoble), 70 (2020) no. 3 p. 1085–1113.Google Scholar
Ancona, M., Critical points of random branched coverings of the Riemann sphere, Math. Z. 296 (2020), 1735–1750.CrossRefGoogle Scholar
Berman, R., Berndtsson, B. and Sjöstrand, J., A direct approach to Bergman kernel asymptotics for positive line bundles, Ark. Mat. 46(2) (2008), 197–217.CrossRefGoogle Scholar
Dai, X., Liu, K. and Ma, X., On the asymptotic expansion of Bergman kernel, J. Differential Geom. 72(1) (2006), 1–41.CrossRefGoogle Scholar
Gayet, D. and Welschinger, J.-Y., Exponential rarefaction of real curves with many components, Publ. Math. Inst. Hautes Études Sci . 113 (2011), 69–96.CrossRefGoogle Scholar
Gayet, D. and Welschinger, J.-Y., What is the total Betti number of a random real hypersurface?, J. Reine Angew. Math. 689 (2014), 137–168.Google Scholar
Gross, B. H. and Harris, J., Real algebraic curves, Ann. Sci. Éc. Norm. Supér. (4), 14(2) (1981), 157–182.CrossRefGoogle Scholar
Kostlan, E., On the distribution of roots of random polynomials, in From Topology to Computation: Proceedings of the Smalefest (Berkeley, CA, 1990), pp. 419–431 (Springer, New York, 1993).CrossRefGoogle Scholar
Ma, X. and Marinescu, G., Holomorphic Morse Inequalities and Bergman Kernels, Progress in Mathematics no. 254 (Birkhäuser Verlag, Basel, 2007).Google Scholar
Shiffman, B. and Zelditch, S., Distribution of zeros of random and quantum chaotic sections of positive line bundles, Comm. Math. Phys. 200(3) (1999), 661–683.CrossRefGoogle Scholar
Shub, M. and Smale, S., Complexity of Bezout’s theorem. II: Volumes and probabilities, in Computational Algebraic Geometry (Nice, 1992), Progress in Mathematics no. 109, pp. 267–285 (Birkhäuser Boston, Boston, 1993).Google Scholar
Tian, G., On a set of polarized Kähler metrics on algebraic manifolds, J. Differential Geom. 32(1) (1990), 99–130.Google Scholar
Zelditch, S., Szegö kernels and a theorem of Tian, Int. Math. Res. Not. IMRN 6 (1998), 317–331.CrossRefGoogle Scholar
Zelditch, S., Large deviations of empirical measures of zeros on Riemann surfaces, Int. Math. Res. Not. IMRN 3 (2013), 592–664.Google Scholar