No CrossRef data available.
 $\mu $-STABILIZERS IN ACF
$\mu $-STABILIZERS IN ACFPublished online by Cambridge University Press: 21 July 2021
We consider G, a linear algebraic group defined over
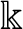 $\Bbbk $
, an algebraically closed field (ACF). By considering
$\Bbbk $
, an algebraically closed field (ACF). By considering
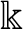 $\Bbbk $
as an embedded residue field of an algebraically closed valued field K, we can associate to it a compact G-space
$\Bbbk $
as an embedded residue field of an algebraically closed valued field K, we can associate to it a compact G-space
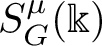 $S^\mu _G(\Bbbk )$
consisting of
$S^\mu _G(\Bbbk )$
consisting of
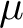 $\mu $
-types on G. We show that for each
$\mu $
-types on G. We show that for each
 $p_\mu \in S^\mu _G(\Bbbk )$
,
$p_\mu \in S^\mu _G(\Bbbk )$
,
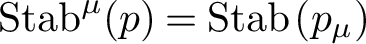 $\mathrm {Stab}^\mu (p)=\mathrm {Stab}\left (p_\mu \right )$
is a solvable infinite algebraic group when
$\mathrm {Stab}^\mu (p)=\mathrm {Stab}\left (p_\mu \right )$
is a solvable infinite algebraic group when
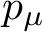 $p_\mu $
is centered at infinity and residually algebraic. Moreover, we give a description of the dimension of
$p_\mu $
is centered at infinity and residually algebraic. Moreover, we give a description of the dimension of
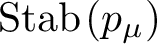 $\mathrm {Stab}\left (p_\mu \right )$
in terms of the dimension of p.
$\mathrm {Stab}\left (p_\mu \right )$
in terms of the dimension of p.