Hostname: page-component-669899f699-8p65j Total loading time: 0 Render date: 2025-04-29T13:48:04.339Z Has data issue: false hasContentIssue false
  • English
  • Français

$(G,\unicode[STIX]{x1D707})$-DISPLAYS AND RAPOPORT–ZINK SPACES

Published online by Cambridge University Press:  19 September 2018

O. Bültel  and
G. Pappas
O. Bültel
Affiliation:
Aldegreverstrasse 28, 45147 Essen, Germany
G. Pappas
Affiliation:
Department of Mathematics, Michigan State University, E. Lansing, MI 48824, USA ([email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 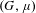$(G,\unicode[STIX]{x1D707})$ be a pair of a reductive group 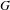$G$ over the 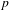$p$-adic integers and a minuscule cocharacter $\unicode[STIX]{x1D707}$ of 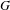$G$ defined over an unramified extension. We introduce and study ‘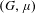$(G,\unicode[STIX]{x1D707})$-displays’ which generalize Zink’s Witt vector displays. We use these to define certain Rapoport–Zink formal schemes purely group theoretically, i.e. without 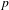$p$-divisible groups.

Keywords

11-XX Number Theory14-XX Algebraic Geometryp-divisible groups
Type
Research Article
Information
Journal of the Institute of Mathematics of Jussieu , Volume 19 , Issue 4 , July 2020 , pp. 1211 - 1257
Check for updates
Copyright
© Cambridge University Press 2018

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

Footnotes

G.P. is partially supported by NSF grants DMS-1360733 and DMS-1701619.

References

Ahsendorf, T., Cheng, C. and Zink, T., 𝓞-displays and 𝜋-divisible formal 𝓞-modules, J. Algebra 457 (2016), 129–193.Google Scholar
Bhatt, B. and Scholze, P., Projectivity of the Witt vector affine Grassmannian, Invent. Math. 209(2) (2017), 329–423.Google Scholar
Bueltel, O., Shimura varieties modulo $p$ with many compact factors, Preprint, 2008, arXiv:0808.4091.Google Scholar
Conrad, B., Gabber, O. and Prasad, G., Pseudo-reductive groups, in New Mathematical Monographs, 2nd ed., Volume 26 (Cambridge University Press, Cambridge, 2015).Google Scholar
Chase, S. U., Direct products of modules, Trans. Amer. Math. Soc. 97 (1960), 457–473.Google Scholar
Conrad, B., Reductive group schemes, in Autour des schémas en groupes. Vol. I, Panor. Synthèses, Volume 42/43, pp. 93–444 (Soc. Math. France, Paris, 2014).Google Scholar
Caraiani, A. and Scholze, P., On the generic part of the cohomology of compact unitary Shimura varieties, Ann. of Math. (2) 186(3) (2017), 649–766.Google Scholar
Colliot-Thélène, J.-L. and Sansuc, J.-J., Fibrés quadratiques et composantes connexes réelles, Math. Ann. 244(2) (1979), 105–134.Google Scholar
Deligne, P., Variétés de Shimura: interprétation modulaire, et techniques de construction de modèles canoniques, in Automorphic Forms, Representations and L-Functions (Proc. Sympos. Pure Math., Oregon State Univ., Corvallis, Ore., 1977), Part 2, Proceedings of Symposia in Pure Mathematics, Volume XXXIII, pp. 247–289 (American Mathematical Society, Providence, RI, 1979).Google Scholar
Demazure, M. and Grothendieck, A., Schémas en groupes. III: Structure des schémas en groupes réductifs, in Séminaire de Géométrie Algébrique du Bois Marie 1962/64 (SGA 3). Dirigé par M. Demazure et A. Grothendieck, Lecture Notes in Mathematics, Volume 153 (Springer, Berlin, 1962/1964).Google Scholar
Fargues, L., Geometrization of the local Langlands correspondence: an overview, Preprint, 2016, arXiv:1602.00999.Google Scholar
Greenberg, M., Schemata over local rings, Ann. of Math. (2) 73 (1961), 624–648.Google Scholar
Grothendieck, A., Éléments de géométrie algébrique. IV. Étude locale des schémas et des morphismes de schémas. I, Inst. Hautes Études Sci. Publ. Math. (20) (1964), 5–259.Google Scholar
Howard, B. and Pappas, G., Rapoport–Zink spaces for spinor groups, Compos. Math. 153(5) (2017), 1050–1118.Google Scholar
Kim, W., Rapoport–Zink spaces of Hodge type, Forum Math. Sigma, to appear, Preprint, 2013, arXiv:1308.5537.Google Scholar
Kottwitz, R., Shimura varieties and twisted orbital integrals, Math. Ann. 269(3) (1984), 287–300.Google Scholar
Kottwitz, R., Isocrystals with additional structure, Compos. Math. 56(2) (1985), 201–220.Google Scholar
Kreidl, M., On p-adic lattices and Grassmannians, Math. Z. 276(3–4) (2014), 859–888.Google Scholar
Lau, E., Displays and formal p-divisible groups, Invent. Math. 171(3) (2008), 617–628.Google Scholar
Rapoport, M. and Richartz, M., On the classification and specialization of F-isocrystals with additional structure, Compos. Math. 103(2) (1996), 153–181.Google Scholar
Rapoport, M. and Viehmann, E., Towards a theory of local Shimura varieties, Münster J. Math. 7(1) (2014), 273–326.Google Scholar
Rapoport, M. and Zink, Th., Period spaces for p-divisible groups, in Annals of Mathematics Studies, Volume 141 (Princeton University Press, Princeton, NJ, 1996).Google Scholar
Rapoport, M. and Zink, T., On the Drinfeld moduli problem of p-divisible groups, Camb. J. Math. 5(2) (2017), 229–279.Google Scholar
Scholze, P., p-adic geometry (lecture course at Berkeley), Preprint, 2014.Google Scholar
Scholze, P. and Weinstein, J., Moduli of p-divisible groups, Camb. J. Math. 1(2) (2013), 145–237.Google Scholar
Zhang, C., Stratifications and foliations for good reductions of Shimura varieties of Hodge type, Preprint, 2015, arXiv:1512.08102.Google Scholar
Zhu, X., Affine Grassmannians and the geometric Satake in mixed characteristic, Ann. of Math. (2) 185(2) (2017), 403–492.Google Scholar
Zink, Th., The display of a formal p-divisible group, Cohomologies p-adiques et applications arithmétiques, I, Astérisque 278 (2002), 127–248.Google Scholar