Hostname: page-component-669899f699-g7b4s Total loading time: 0 Render date: 2025-04-27T19:00:50.689Z Has data issue: false hasContentIssue false
  • English
  • Français

BANACH SPACES IN WHICH LARGE SUBSETS OF SPHERES CONCENTRATE

Part of: Linear function spaces and their duals Normed linear spaces and Banach spaces; Banach lattices Set theory Fairly general properties

Published online by Cambridge University Press:  27 December 2022

Piotr Koszmider Open the ORCID record for Piotr Koszmider [Opens in a new window]
Piotr Koszmider*
Affiliation:
Institute of Mathematics of the Polish Academy of Sciences, ul. Śniadeckich 8, 00-656 Warszawa, Poland
*
([email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

We construct a nonseparable Banach space 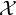$\mathcal {X}$ (actually, of density continuum) such that any uncountable subset 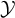$\mathcal {Y}$ of the unit sphere of 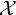$\mathcal {X}$ contains uncountably many points distant by less than 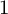$1$ (in fact, by less then 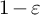$1-\varepsilon $ for some 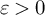$\varepsilon>0$). This solves in the negative the central problem of the search for a nonseparable version of Kottman’s theorem which so far has produced many deep positive results for special classes of Banach spaces and has related the global properties of the spaces to the distances between points of uncountable subsets of the unit sphere. The property of our space is strong enough to imply that it contains neither an uncountable Auerbach system nor an uncountable equilateral set. The space is a strictly convex renorming of the Johnson–Lindenstrauss space induced by an 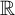$\mathbb {R}$-embeddable almost disjoint family of subsets of 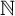$\mathbb {N}$. We also show that this special feature of the almost disjoint family is essential to obtain the above properties.

MSC classification

Primary: 46B20: Geometry and structure of normed linear spaces 03E75: Applications of set theory 46B26: Nonseparable Banach spaces
Secondary: 46E15: Banach spaces of continuous, differentiable or analytic functions 54D80: Special constructions of spaces (spaces of ultrafilters, etc.)
Type
Research Article
Information
Journal of the Institute of Mathematics of Jussieu , Volume 23 , Issue 2 , March 2024 , pp. 737 - 752
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Baronti, M., Casini, E. and Papini, P. L., ‘On average distances and the geometry of Banach spaces’, Nonlinear Anal. Ser. A: Theory Methods 42(3) (2000), no. 3, 533–541.CrossRefGoogle Scholar
Cabello Sánchez, F., Castillo, J. M. F., Marciszewski, W., Plebanek, G. and Salguero-Alarcón, A., ‘Sailing over three problems of Koszmide’, J. Funct. Anal. 279(4) (2020), 108571.CrossRefGoogle Scholar
Castillo, J. M. F., González, M. and Papini, P. L., ‘New results on Kottman’s constant’, Banach J. Math. Anal. 11(2) (2017), 348–362.CrossRefGoogle Scholar
Castillo, J. M. F., González, M., Kania, T. and Papini, P. L., The isomorphic Kottman constant, Proc. AMS, 148 (2020), 4361–4375.CrossRefGoogle Scholar
Cúth, M., Kurka, O. and Vejnar, B., Large separated sets of unit vectors in Banach spaces of continuous functions, Colloq. Math. 157(2) (2019), 173–187.CrossRefGoogle Scholar
Day, M., ‘On the basis problem in normed spaces’, Proc. Amer. Math. Soc. 13 (1962), 655–658.CrossRefGoogle Scholar
Deville, R., Godefroy, G. and Zizler, V., ‘Smoothness and Renormings in Banach Spaces’, Pitman Monographs and Surveys in Pure and Applied Mathematics, 64 (Longman Scientific & Technical, Harlow; copublished in the United States with John Wiley & Sons, Inc., New York, 1993).Google Scholar
Dow, A., ‘Sequential order under PFA. Canad. Math. Bull. 54(2) (2011), 270–276.CrossRefGoogle Scholar
Elton, J. and Odell, E., ‘The unit ball of every infinite-dimensional normed linear space contains a $\left(1+\varepsilon \right)$ -separated sequence’, Colloq. Math. 44 (1981), 105–109.CrossRefGoogle Scholar
Freeman, D., Odell, E., Sari, B. and Schlumprecht, T., ‘Equilateral sets in uniformly smooth Banach spaces’, Mathematika 60(1) (2014), 219–231.CrossRefGoogle Scholar
Glakousakis, E. and Mercourakis, S., ‘Examples of infinite dimensional Banach spaces without infinite equilateral sets’, Serdica Math. J. 42(1) (2016), 65–88.Google Scholar
Godefroy, G. and Talagrand, M., ‘Espaces de Banach représentables’, Israel J. Math. 41(4) (1982),–330.CrossRefGoogle Scholar
Godun, B. V., ‘A special class of Banach spaces’, Mat. Zametki 37(3) (1985), 391–398, 462.Google Scholar
Godun, B. V., ‘Auerbach bases in Banach spaces that are isomorphic to ${\ell}_1{\left[0,1\right]}$ ’, C. R. Acad. Bulgare Sci. 43(10) (1990), 19–21.Google Scholar
Godun, B. V., Lin, B. and Troyanski, S., On Auerbach Bases. Banach Spaces (Mérida, 1992) , Contemp. Math., 144, (Amer. Math. Soc., Providence, RI, 1993) 115–118.Google Scholar
Guirao, A., Montesinos, V. and Zizler, V., Open Problems in the Geometry and Analysis of Banach Spaces (Springer, Cham, 2016).CrossRefGoogle Scholar
Guzmán, O., Hrušák, M. and Koszmider, P., ‘On $\mathbb{R}$ -embeddability of almost disjoint families and Akemann-Doner C $\ast$ -algebras’, Fund. Math. 254(1) (2021), 15–47.CrossRefGoogle Scholar
Hájek, P., Montesinos Santalucía, V., Vanderwerff, J. and Zizler, V., Biorthogonal Systems in Banach Spaces , CMS Books in Mathematics/Ouvrages de Mathématiques de la SMC , vol. 26 (Springer, New York, 2008).Google Scholar
Hájek, P., Kania, T. and Russo, T., ‘Separated sets and Auerbach systems in Banach spaces’, Trans. Amer. Math. Soc. 373(10) (2020), 6961–6998.CrossRefGoogle Scholar
Hrušák, M. and Guzmán, O., ‘n-Luzin gaps’, Topology Appl. 160(12) (2013), 1364–1374.CrossRefGoogle Scholar
Hrušák, M., Almost Disjoint Families and Topology. Recent Progress in General Topology. III (Atlantis Press, Paris, 2014), 601–638.Google Scholar
Jech, T., Set Theory, third millennium edn., revised and expanded, Springer Monographs in Mathematics (Springer-Verlag, Berlin, 2003).Google Scholar
Johnson, W. B. and Lindenstrauss, J., ‘Some remarks on weakly compactly generated Banach spaces’, Israel J. Math. 17 (1974), 219–230.CrossRefGoogle Scholar
Johnson, W. B. and Lindenstrauss, J., ‘Correction to: “Some remarks on weakly compactly generated Banach spaces”’, Israel J. Math. 32(4) (1979), 382–383.CrossRefGoogle Scholar
Kania, T. and Kochanek, T., ‘Uncountable sets of unit vectors that are separated by more than $1$ ’, Studia Math. 232(1) (2016), 19–44.Google Scholar
Komjáth, P. and Totik, V., Problems and Theorems in Classical Set Theory , Problem Books in Mathematics (Springer, New York, 2006).Google Scholar
Koszmider, P., ‘Uncountable equilateral sets in Banach spaces of the form $C{(K)}$ ’, Israel J. Math. 224(1) (2018), 83–103.CrossRefGoogle Scholar
Koszmider, P. and Laustsen, N. J., ‘A Banach space induced by an almost disjoint family, admitting only few operators and decompositions’, Adv. Math. 381 (2021), 107613.CrossRefGoogle Scholar
Koszmider, P. and Wark, H. M., ‘Large Banach spaces with no infinite equilateral sets’, Bull. Lond. Math. Soc. 54(6) (2022), 2066–2077.CrossRefGoogle Scholar
Kottman, C., ‘Subsets of the unit ball that are separated by more than one’, Studia Math. 53(1) (1975), 15–27.CrossRefGoogle Scholar
Kottman, C., ‘Packing and reflexivity in Banach spaces’, Trans. Amer. Math. Soc. 150 (1970), 565–576.CrossRefGoogle Scholar
Kryczka, A. and Prus, S., ‘Separated sequences in nonreflexive Banach spaces’, Proc. Amer. Math. Soc. 129(1) (2001), 155–163.CrossRefGoogle Scholar
Luzin, N. N., ‘On subsets of the series of natural numbers’, Izvestiya Akad. Nauk SSSR. Ser.Mat. 11 (1947), 403–410 Google Scholar
Maluta, E. and Papini, P. L., ‘Estimates for Kottman’s separation constant in reflexive Banach spaces’, Colloq. Math. 117(1) (2009), 105–119.CrossRefGoogle Scholar
Marciszewski, W. and Pol, R., ‘On Banach spaces whose norm-open sets are ${F}_{\sigma }$ -sets in the weak topology’, J. Math. Anal. Appl. 350(2) (2009), 708–722.CrossRefGoogle Scholar
Marciszewski, W. and Pol, R., ‘On Borel almost disjoint families’, Monatshefte Math. 168 (2012) 545–562.CrossRefGoogle Scholar
Mercourakis, S. and Vassiliadis, G., ‘Equilateral sets in infinite dimensional Banach spaces’, Proc. Amer. Math. Soc. 142(1) (2014), 205–212.CrossRefGoogle Scholar
Mercourakis, S. and Vassiliadis, G., ‘Equilateral sets in Banach spaces of the form $C{(K)}$ ’, Studia Math. 231(3) (2015), 241–255.Google Scholar
Mercourakis, S. and Vassiliadis, G., ‘Isometric embeddings of a class of separable metric spaces into Banach spaces’, Comment. Math. Univ. Carolin. 59(2) (2018), 233–239.Google Scholar
van Neerven, J., ‘Separated sequences in uniformly convex Banach spaces’, Colloq. Math. 102(1) (2005), 147–153.CrossRefGoogle Scholar
Papini, P. L., ‘Bad normed spaces, convexity properties, separated sets’, Nonlinear Anal. 73(6) (2010), 1491–1494.CrossRefGoogle Scholar
Pełczyński, A., Semadeni, Z., ‘Spaces of continuous functions (III) (Spaces $C(\varOmega)$ for $\varOmega$ without perfect subsets)’, Studia Math. 18 (1959), 211–222.CrossRefGoogle Scholar
Pličko, A., ‘On bounded biorthogonal systems in some function spaces’, Studia Math. 84 (1986), 25–37.CrossRefGoogle Scholar
Riesz, F., ‘Über lineare Funktionalgleichungen’, Acta Math. 41 (1916), 71–98.CrossRefGoogle Scholar
Russo, T., ‘A note on symmetric separation in Banach spaces’, RACSAM 113 (4) (2019), 3649–3658.CrossRefGoogle Scholar
Shkarin, S., ‘Isometric embedding of finite ultrametric spaces in Banach spaces’, Topology Appl. 142(1–3) (2004), 13–17.CrossRefGoogle Scholar
Terenzi, P., ‘Successioni regolari negli spazi di Banach’, Rend. Sem. Mat. Fis. Milano 57 1 (1987), 275–285.CrossRefGoogle Scholar
Terenzi, P., ‘Equilater sets in Banach spaces’, Boll. Un. Mat. Ital. A (7) 3(1) (1989), 119–124.Google Scholar