Hostname: page-component-669899f699-8p65j Total loading time: 0 Render date: 2025-04-30T11:25:48.444Z Has data issue: false hasContentIssue false
  • English
  • Français

ON THE DISTINCTION OF IWAHORI-SPHERICAL DISCRETE SERIES REPRESENTATIONS

Part of: Representation theory of groups Lie groups Discontinuous groups and automorphic forms

Published online by Cambridge University Press:  17 April 2024

Paul Broussous Open the ORCID record for Paul Broussous [Opens in a new window]
Paul Broussous*
Affiliation:
Laboratoire de Mathématiques et Applications, UMR 7348 du CNRS, Site du Futuroscope – Téléport 2, 11, Boulevard Marie et Pierre Curie, Bâtiment H3 – TSA 61125, 86073 POITIERS CEDEX, France
*
[email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Let $E/F$ be a quadratic unramified extension of non-archimedean local fields and $\mathbb H$ a simply connected semisimple algebraic group defined and split over F. We establish general results (multiplicities, test vectors) on ${\mathbb H} (F)$-distinguished Iwahori-spherical representations of 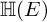${\mathbb H} (E)$. For discrete series Iwahori-spherical representations of 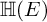${\mathbb H} (E)$, we prove a numerical criterion of ${\mathbb H} (F)$-distinction. As an application, we classify the ${\mathbb H} (F)$-distinguished discrete series representations of ${\mathbb H} (E)$ corresponding to degree $1$ characters of the Iwahori-Hecke algebra.

Keywords

reductive groups over local fieldsrelative Langlands programreductive symmetric spacesIwahori-Hecke algebras

MSC classification

Primary: 22E50: Representations of Lie and linear algebraic groups over local fields 22E35: Analysis on $p$-adic Lie groups 11F70: Representation-theoretic methods; automorphic representations over local and global fields
Secondary: 20C08: Hecke algebras and their representations
Type
Research Article
Information
Journal of the Institute of Mathematics of Jussieu , Volume 24 , Issue 1 , January 2025 , pp. 1 - 15
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Beuzart-Plessis, R., On distinguished square-integrable representations for Galois pairs and a conjecture of Prasad, Invent. Math. 214(1) (2018), 437–521.CrossRefGoogle Scholar
Borel, A., Admissible representations of a semi-simple group over a local field with vectors fixed under an Iwahori subgroup, Invent. Math. 35 (1976), 233–259.CrossRefGoogle Scholar
Bott, R., An application of the Morse theory to the topology of Lie-groups, Bull. Soc. Math. France 84 (1956), 251–281.CrossRefGoogle Scholar
Bourbaki, N., Groupes et algèbres de Lie (Paris, Hermann, 1968), Chap. IV, V, VI.Google Scholar
Broussous, P., Explicit matrix coefficients and test vectors for discrete series representations, arXiv:2005.02904v2.Google Scholar
Broussous, P. and Courtès, F., Distinction of the Steinberg representation, Int. Math. Res. Not. IMRN 2014(11), 3140–3157. With an appendix by François Courtès.CrossRefGoogle Scholar
Bushnell, C. J. and Kutzko, P. C., Smooth representations of reductive $p$ -adic groups: structure theory via types, Proc. London Math. Soc. 77(3) (1998), 582–634.CrossRefGoogle Scholar
Casselman, W., The unramified principal series of $p$ -adic groups. I. The spherical function, Compos. Math. 40(3) (1980), 387–406.Google Scholar
Courtès, F., Distinction of the Steinberg representation II: an equality of characters, Forum Math. 27(6) (2015), 346–3475.CrossRefGoogle Scholar
Gurevich, M. and Offen, O., A criterion of integrability of matrix coefficients with respect to a symmetric space, J. Funct. Anal. 270(12) (2016), 4478–4512.CrossRefGoogle Scholar
Gyoja, A., A generalised Poincaré series associated to a Hecke algebra of a finite or $p$ -adic Chevalley group, Japan J. Math. 9(1), 1983.CrossRefGoogle Scholar
Iwahori, N., Generalized Tits system (Bruhat decomposition) on $p$ -adic semisimple groups, in Algebraic Groups and Discontinuous Subgroups (Proc. Sympos. Pure Math., Boulder, CO, 1965) (Amer. Math. Soc., Providence, RI, 1966), 71–83.CrossRefGoogle Scholar
Kazhdan, D. and Lusztig, G., Proof of the Deligne Langlands conjecture for Hecke algebras, Invent. Math. 87(1) (1987), 153–215.CrossRefGoogle Scholar
Macdonald, I. G., The Poincaré series of a Coxeter group, Math. Ann. 199 (1972), 161–174.CrossRefGoogle Scholar
Prasad, D., On a conjecture of Jacquet about distinguished representations of GL(n), Duke Math. J. 109(1) (2001), 67–78.CrossRefGoogle Scholar
Prasad, D., A ‘relative’ local Langlands correspondence, arXiv:1512.04347v1.Google Scholar
Reeder, M., On the Iwahori-spherical discrete series for $p$ -adic Chevalley groups; formal degrees and $L$ -packets, Ann. Sci. École Norm. Sup. (4) 27(4) (1994), 463–491.CrossRefGoogle Scholar
Steinberg, R., Endomorphisms of Linear Algebraic Groups (Memoirs of the American Mathematical Society) no. 80 (American Mathematical Society, Providence, RI, 1968), 108 pp.CrossRefGoogle Scholar
Zhang, C., Local periods for discrete series representations, J. Funct. Anal. 271(6) (2016), 1525–1543.CrossRefGoogle Scholar