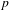Hostname: page-component-669899f699-tpknm Total loading time: 0 Render date: 2025-04-30T20:00:57.571Z Has data issue: false hasContentIssue false
  • English
  • Français

A DEFINABLE $p$-ADIC ANALOGUE OF KIRSZBRAUN’S THEOREM ON EXTENSIONS OF LIPSCHITZ MAPS

Part of: Model theory Topological fields Algebraic number theory: local and $p$-adic fields

Published online by Cambridge University Press:  20 October 2015

Raf Cluckers  and
Florent Martin
Raf Cluckers
Affiliation:
Université de Lille, Laboratoire Painlevé, CNRS - UMR 8524, Cité Scientifique, 59655 Villeneuve d’Ascq Cedex, France KU Leuven, Department of Mathematics, Celestijnenlaan 200B, B-3001 Leuven, Belgium ([email protected]) URL http://math.univ-lille1.fr/∼cluckers
Florent Martin
Affiliation:
Fakultät für Mathematik, Universität Regensburg, 93040 Regensburg, Germany ([email protected]) URL http://homepages.uni-regensburg.de/∼maf55605/
Get access Rights & Permissions [Opens in a new window]

Abstract

A direct application of Zorn’s lemma gives that every Lipschitz map 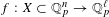$f:X\subset \mathbb{Q}_{p}^{n}\rightarrow \mathbb{Q}_{p}^{\ell }$ has an extension to a Lipschitz map 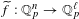$\widetilde{f}:\mathbb{Q}_{p}^{n}\rightarrow \mathbb{Q}_{p}^{\ell }$. This is analogous to, but easier than, Kirszbraun’s theorem about the existence of Lipschitz extensions of Lipschitz maps 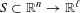$S\subset \mathbb{R}^{n}\rightarrow \mathbb{R}^{\ell }$. Recently, Fischer and Aschenbrenner obtained a definable version of Kirszbraun’s theorem. In this paper, we prove in the 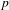$p$-adic context that 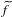$\widetilde{f}$ can be taken definable when 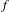$f$ is definable, where definable means semi-algebraic or subanalytic (or some intermediary notion). We proceed by proving the existence of definable Lipschitz retractions of 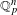$\mathbb{Q}_{p}^{n}$ to the topological closure of 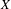$X$ when 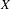$X$ is definable.

Keywords

p-adic semi-algebraic functionsp-adic subanalytic functionsLipschitz continuous functionsp-adic cell decompositiondefinable retractions

MSC classification

Primary: 03C98: Applications of model theory 12J25: Non-Archimedean valued fields
Secondary: 03C60: Model-theoretic algebra 11S80: Other analytic theory (analogues of beta and gamma functions, $p$-adic integration, etc.)
Type
Research Article
Information
Journal of the Institute of Mathematics of Jussieu , Volume 17 , Issue 1 , February 2018 , pp. 39 - 57
Copyright
© Cambridge University Press 2015 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Aschenbrenner, M. and Fischer, A., Definable versions of theorems by Kirszbraun and Helly, Proc. Lond. Math. Soc. (3) 102(3) (2011), 468–502.Google Scholar
Bhaskaran, R., The structure of ideals in the Banach algebra of Lipschitz functions over valued fields, Compos. Math. 48(1) (1983), 25–34.Google Scholar
Cluckers, R., Presburger sets and p-minimal fields, J. Symbolic Logic 68 (2003), 153–162.Google Scholar
Cluckers, R., Comte, G. and Loeser, F., Lipschitz continuity properties for p-adic semi-algebraic and subanalytic functions, Geom. Funct. Anal. 20(1) (2010), 68–87.CrossRefGoogle Scholar
Cluckers, R. and Halupczok, I., Approximations and Lipschitz continuity in p-adic semi-algebraic and subanalytic geometry, Selecta Math. (N.S.) 18(4) (2012), 825–837.Google Scholar
Cluckers, R. and Lipshitz, L., Fields with analytic structure, J. Eur. Math. Soc. (JEMS) 13(4) (2011), 1147–1223.CrossRefGoogle Scholar
Cohen, P. J., Decision procedures for real and p-adic fields, Comm. Pure Appl. Math. 22 (1969), 131–151.CrossRefGoogle Scholar
Darnière, L. and Halupczok, I., Cell decomposition and classification of definable sets in $p$ -optimal fields (2015) arXiv:1412.2571.Google Scholar
Denef, J., The rationality of the Poincaré series associated to the p-adic points on a variety, Invent. Math. 77 (1984), 1–23.Google Scholar
Denef, J., p-adic semialgebraic sets and cell decomposition, J. Reine Angew. Math. 369 (1986), 154–166.Google Scholar
Denef, J. and van den Dries, L., p-adic and real subanalytic sets, Ann. of Math. (2) 128(1) (1988), 79–138.Google Scholar
van den Dries, L., Algebraic theories with definable Skolem functions, J. Symbolic Logic 49(2) (1984), 625–629.Google Scholar
Halupczok, I., Trees of definable sets over the p-adics, J. Reine Angew. Math. 642 (2010), 157–196.Google Scholar
Halupczok, I., Trees of definable sets in ℤ p , in Motivic Integration and its Interactions with Model Theory and Non-Archimedean Geometry, Vol. II, London Mathematical Society Lecture Note Series, 384, pp. 87–107 (Cambridge University Press, Cambridge, 2011).Google Scholar
Haskell, D. and Macpherson, D., A version of o-minimality for the p-adics, J. Symbolic Logic 62(4) (1997), 1075–1092.CrossRefGoogle Scholar
Kirszbraun, M. D., Über die zusammenziehende und Lipschitzsche Transformationen, Fund. Math. 22 (1934), 77–108.Google Scholar
Kuijpers, T., Lipschitz extensions of definable p-adic functions, Math. Log. Q. 61(3) (2015), 151–158.Google Scholar
Macintyre, A., On definable subsets of p-adic fields, J. Symbolic Logic 41 (1976), 605–610.Google Scholar
Margalef Roig, J. and Outerelo Domínguez, E., Differential Topology, North-Holland Mathematics Studies, 173, (North-Holland Publishing Co., Amsterdam, 1992). With a preface by P. W. Michor.Google Scholar
McShane, E. J., Extension of range of functions, Bull. Amer. Math. Soc. 40 (1934), 837–842.Google Scholar
Pas, J., Cell decomposition and local zeta functions in a tower of unramified extensions of a p-adic field, Proc. Lond. Math. Soc. (3) 60(1) (1990), 37–67.Google Scholar
Presburger, M., On the completeness of a certain system of arithmetic of whole numbers in which addition occurs as the only operation, Hist. Philos. Logic 12(2) (1991), 225–233.Google Scholar
Whitney, H., Analytic extensions of functions defined in closed sets, Trans. Amer. Math. Soc. 36 (1934), 63–89.CrossRefGoogle Scholar