Hostname: page-component-669899f699-cf6xr Total loading time: 0 Render date: 2025-04-27T12:18:45.467Z Has data issue: false hasContentIssue false
  • English
  • Français

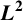A WEIGHTED $\boldsymbol {L}^{\boldsymbol {2}}$ ESTIMATE OF COMMUTATORS OF BOCHNER–RIESZ OPERATORS FOR HERMITE OPERATOR

Part of: Harmonic analysis in several variables Partial differential operators

Published online by Cambridge University Press:  15 January 2024

PENG CHEN  and
XIXI LIN
PENG CHEN
Affiliation:
Department of Mathematics, Sun Yat-sen University, Guangzhou 510275, PR China e-mail: [email protected]
XIXI LIN*
Affiliation:
Department of Mathematics, Sun Yat-sen University, Guangzhou 510275, PR China
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Let H be the Hermite operator 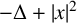$-\Delta +|x|^2$ on 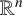$\mathbb {R}^n$. We prove a weighted 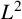$L^2$ estimate of the maximal commutator operator 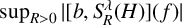$\sup _{R>0}|[b, S_R^\lambda (H)](f)|$, where 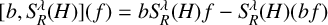$ [b, S_R^\lambda (H)](f) = bS_R^\lambda (H) f - S_R^\lambda (H)(bf) $ is the commutator of a BMO function b and the Bochner–Riesz means 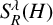$S_R^\lambda (H)$ for the Hermite operator H. As an application, we obtain the almost everywhere convergence of 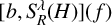$[b, S_R^\lambda (H)](f)$ for large 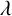$\lambda $ and $f\in L^p(\mathbb {R}^n)$.

Keywords

weighted L2 estimatecommutatorsBochner–Riesz operatorsHermite operator

MSC classification

Primary: 42B15: Multipliers
Secondary: 42B25: Maximal functions, Littlewood-Paley theory 47F05: Partial differential operators (should also be assigned at least one other classification number in section 47)
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 116 , Issue 3 , June 2024 , pp. 308 - 330
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

Footnotes

Communicated by Ji Li

P. Chen and X. Lin were supported by National Key R&D Program of China 2022YFA1005702. P. Chen was supported by NNSF of China 12171489, Guangdong Natural Science Foundation 2022A1515011157.

References

Álvarez, J., Bagby, R. J., Kurtz, D. S. and Pérez, C., ‘Weighted estimates for commutators of linear operators’, Studia Math. 104(2) (1993), 195–209.CrossRefGoogle Scholar
Bergh, J. and Löfström, J., Interpolation Spaces, an Introduction (Springer-Verlag, New York, 1976).CrossRefGoogle Scholar
Bui, T. A., ‘Weighted norm inequalities for spectral multipliers without Gaussian estimates’, Tokyo J. Math. 37(2) (2014), 373–384.CrossRefGoogle Scholar
Chen, P., Duong, X. T., He, D., Lee, S. and Yan, L. X., ‘Almost everywhere convergence of Bochner–Riesz means for the Hermite operators’, Adv. Math. (2021), Article no. 108042, 42 pages.CrossRefGoogle Scholar
Chen, P., Lee, S., Sikora, A. and Yan, L. X., ‘Bounds on the maximal Bochner–Riesz means for elliptic operators’, Trans. Amer. Math. Soc. 373(6) (2020), 3793–3828.CrossRefGoogle Scholar
Chen, P., Lin, X. and Yan, L. X., ‘The commutators of Bochner–Riesz operators for Hermite operator’, J. Geom. Anal. 33 (2023), 87.CrossRefGoogle Scholar
Chen, P., Ouhabaz, E. M., Sikora, A. and Yan, L. X., ‘Restriction estimates, sharp spectral multipliers and endpoint estimates for Bochner–Riesz means’, J. Anal. Math. 129 (2016), 219–283.10.1007/s11854-016-0021-0CrossRefGoogle Scholar
Coifman, R. R., Lions, P. L., Meyer, Y. and Semmes, S., ‘Compensated compactness and Hardy spaces’, J. Math. Pures Appl. (9) 72(3) (1993), 247–286.Google Scholar
Coifman, R. R., Rochberg, R. and Weiss, G., ‘Factorization theorems for Hardy spaces in several variables’, Ann. of Math. (2) 103(3) (1976), 611–635.10.2307/1970954CrossRefGoogle Scholar
Duong, X. T., Ouhabaz, E. M. and Sikora, A., ‘Plancherel-type estimates and sharp spectral multipliers’, J. Funct. Anal. 196 (2002), 443–485.CrossRefGoogle Scholar
Duong, X. T., Sikora, A. and Yan, L. X., ‘Weighted norm inequalities, Gaussian bounds and sharp spectral multipliers’, J. Funct. Anal. 260(4) (2011), 1106–1131.10.1016/j.jfa.2010.11.006CrossRefGoogle Scholar
Ferguson, S. H. and Lacey, M. T., ‘A characterization of product BMO by commutators’, Acta Math. 189(2) (2002), 143–160.CrossRefGoogle Scholar
Garcia-Cuerva, J., Harboure, E., Segovia, C. and Torre, J. L., ‘Weighted norm inequalities for commutators of strongly singular integrals’, Indiana Univ. Math. J. 40 (1991), 1397–1420.CrossRefGoogle Scholar
Holmes, I., Lacey, M. T. and Wick, B. D., ‘Commutators in the two-weight setting’, Math. Ann. 367(1–2) (2017), 51–80.CrossRefGoogle Scholar
Hu, G. E. and Lu, S. Z., ‘The commutator of the Bochner–Riesz operator’, Tohoku Math. J. (2) 48(2) (1996), 259–266.CrossRefGoogle Scholar
Hu, G. E. and Lu, S. Z., ‘The maximal operator associated with the Bochner–Riesz operator’, Beijing Math. 2:1(2) (1996), 96–106.Google Scholar
Hu, G. E. and Lu, S. Z., ‘A weighted ${L}^2$ estimate for the commutator of the Bochner–Riesz operator’, Proc. Amer. Math. Soc. 125 (1997), 2867–2873.CrossRefGoogle Scholar
Hytönen, T. P., ‘The ${L}^p$ -to- ${L}^q$ boundedness of commutators with applications to the Jacobian operator’, J. Math. Pures Appl. (9) 156 (2021), 351–391.CrossRefGoogle Scholar
Karadzhov, G. E., ‘Riesz summability of multiple Hermite series in ${L}^p$ spaces’, C. R. Acad. Bulgare Sci. 47(2) (1994), 5–8.Google Scholar
Lacey, M. T., Petermichl, S., Pipher, J. C. and Wick, B. D., ‘Multiparameter Riesz commutators’, Amer. J. Math. 131(3) (2009), 731–769.CrossRefGoogle Scholar
Lacey, M. T., Petermichl, S., Pipher, J. C. and Wick, B. D., ‘Multi-parameter Div–Curl lemmas’, Bull. Lond. Math. Soc. 44(6) (2012), 1123–1131.CrossRefGoogle Scholar
Lee, S. and Ryu, J., ‘Bochner–Riesz means for the Hermite and special Hermite expansions’, Adv. Math. 400 (2022), Article no. 108260, 52 pages.CrossRefGoogle Scholar
Nazarov, F., Pisier, G., Treil, S. and Volberg, A., ‘Sharp estimates in vector Carleson imbedding theorem and for vector paraproducts’, J. reine angew. Math. 542 (2002), 147–171.Google Scholar
Ouhabaz, E. M., Analysis of Heat Equations on Domains, London Mathematical Society Monographs Series, 31 (Princeton University Press, Princeton, NJ, 2005).Google Scholar
Sikora, A., ‘Riesz transform, Gaussian bounds and the method of wave equation’, Math. Z. 247(3) (2004), 643–662.CrossRefGoogle Scholar
Stein, E. M. and Weiss, G., ‘Interpolation of operators with change of measures’, Trans. Amer. Math. Soc. 87 (1958), 159–172.CrossRefGoogle Scholar
Stein, E. M. and Weiss, G., Introduction to Fourier Analysis on Euclidean Spaces (Princeton University Press, Princeton, NJ, 1971).Google Scholar
Thangavelu, S., ‘Summability of Hermite expansions I’, Trans. Amer. Math. Soc. 314(1) (1989), 119–142.10.1090/S0002-9947-1989-99923-2CrossRefGoogle Scholar
Thangavelu, S., ‘Summability of Hermite expansions II’, Trans. Amer. Math. Soc. 314(1) (1989), 143–170.CrossRefGoogle Scholar
Thangavelu, S., ‘Hermite and special Hermite expansions revisited’, Duke Math. J. 94(2) (1998), 257–278.CrossRefGoogle Scholar
Uchiyama, A., ‘On the compactness of operators of Hankel type’, Tohoku Math. J. (2) 30(1) (1978), 163–171.CrossRefGoogle Scholar
Uchiyama, A., ‘The factorization of ${H}^p$ on the space of homogeneous type’, Pacific J. Math. 92(2) (1981), 453–468.CrossRefGoogle Scholar