Hostname: page-component-669899f699-7xsfk Total loading time: 0 Render date: 2025-04-27T10:20:32.268Z Has data issue: false hasContentIssue false
  • English
  • Français

TWISTED ACTIONS ON COHOMOLOGIES AND BIMODULES

Part of: Linear algebraic groups and related topics Homology and cohomology theories

Published online by Cambridge University Press:  31 May 2024

VLADIMIR SHCHIGOLEV Open the ORCID record for VLADIMIR SHCHIGOLEV [Opens in a new window]
VLADIMIR SHCHIGOLEV*
Affiliation:
Financial University under the Government of the Russian Federation, Leningradsky Prospekt, 49/2, Moscow 125993, Russia
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

For closed subgroups L and R of a compact Lie group G, a left L-space X, and an L-equivariant continuous map 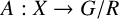$A:X\to G/R$, we introduce the twisted action of the equivariant cohomology 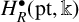$H_R^{\bullet }(\mathrm {pt},\Bbbk )$ on the equivariant cohomology 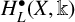$H_L^{\bullet }(X,\Bbbk )$. Considering this action as a right action, 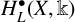$H_L^{\bullet }(X,\Bbbk )$ becomes a bimodule together with the canonical left action of 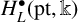$H_L^{\bullet }(\mathrm {pt},\Bbbk )$. Using this bimodule structure, we prove an equivariant version of the Künneth isomorphism. We apply this result to the computation of the equivariant cohomologies of Bott–Samelson varieties and to a geometric construction of the bimodule morphisms between them.

Keywords

equivariant cohomologyfiber bundleKünneth isomorphismBott–Samelson varietydiagrams

MSC classification

Primary: 55N91: Equivariant homology and cohomology
Secondary: 20G05: Representation theory
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 117 , Issue 2 , October 2024 , pp. 187 - 238
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

Footnotes

Communicated by Oded Yacobi

References

Anderson, D. and Fulton, W., Equivariant Cohomology in Algebraic Geometry, Cambridge Studies in Advanced Mathematics, 210 (Cambridge University Press, Cambridge, 2023).CrossRefGoogle Scholar
Borel, A., ‘Sur la cohomolgie des espaces fibrés principaux et des espaces homogénes de group de Lie compact’, Ann. of Math. (2) 57 (1953), 115–207.CrossRefGoogle Scholar
Brion, M., ‘Equivariant cohomology and equivariant intersection theory’, in: Representation Theories and Algebraic Geometry, Nato ASIC Series, 514 (eds. Broer, A., Daigneault, A. and Sabidussi, G.) (Springer, Dordrecht, 1998), 1–37.Google Scholar
Bott, R. and Samelson, H., ‘Application of the theory of Morse to the symmetric spaces’, Amer. J. Math. 80 (1958), 964–1029.CrossRefGoogle Scholar
Dimca, A., Sheaves in Topology, Universitext (Springer, Berlin, 2004).CrossRefGoogle Scholar
Dugundji, J., Topology (Allyn and Bacon, Boston, 1966).Google Scholar
Elias, B., ‘The two-color Soergel calculus’, Compos. Math. 152(2) (2016), 327–398.CrossRefGoogle Scholar
Elias, B. and Khovanov, M., ‘Diagrammatics for Soergel categories’, Int. J. Math. Math. Sci. (2010), 978635.CrossRefGoogle Scholar
Elias, B. and Williamson, G., ‘Soergel calculus’, Represent. Theory 20 (2016), 295–374.CrossRefGoogle Scholar
Fulton, W., ‘Equivariant cohomology in algebraic topology’, Lectures at Columbia University, Eilenberg Lectures, 2007. https://people.math.osu.edu/anderson.2804/eilenberg/.Google Scholar
Grossberg, M. and Karshon, Y., ‘Bott towers, complete integrability, and the extended character of representations’, Duke Math. J. 76(1) (1994), 23–58.CrossRefGoogle Scholar
Hatcher, A., Algebraic Topology (Cambridge University Press, Cambridge, 2002).Google Scholar
Husemoeller, D., Fibre Bundles, 3rd edn, Graduate Texts in Mathematics, 20 (Springer, New York, 1994).CrossRefGoogle Scholar
Iversen, B., Cohomology of Sheaves, Universitext (Springer, Berlin–Heidelberg–New York, 1986).CrossRefGoogle Scholar
Jantzen, J. C., ‘Moment graphs and representations’, in: Geometric Methods in Representation Theory, Summer School Proceedings (Institut Fourier, Grenoble, France, 2008).Google Scholar
Kashiwara, M. and Schapira, P., Sheaves on Manifolds, Grundlehren der mathematischen Wissenschaften, 292 (Springer, Berlin–Heidelberg–New York, 1990).CrossRefGoogle Scholar
Lee, J. M., Introduction to Smooth Manifolds, 2nd edn, Graduate Texts in Mathematics, 218 (Springer, New York, 2013).Google Scholar
Libedinsky, N., ‘Sur la catégorie des bimodules de Soergel’, J. Algebra 320 (2008), 2675–2694.CrossRefGoogle Scholar
Rotman, J., An Introduction to Homological Algebra (Academic Press, New York, 1979).Google Scholar
Riche, S. and Williamson, G., ‘Tilting modules and the p-canonical basis’, Astérisque 397 (2018), ix+184pp.CrossRefGoogle Scholar
Shchigolev, V., ‘Bases of $T$ -equivariant cohomology of Bott–Samelson varieties’, J. Aust. Math. Soc. 104(1) (2018), 80–126.CrossRefGoogle Scholar
Shchigolev, V., ‘Nested fibre bundles in Bott–Samelson varieties’, J. Algebra 605 (2022), 296–338.CrossRefGoogle Scholar
Steinberg, R., Lectures on Chevalley Groups (American Mathematical Society, New Haven, 1968).Google Scholar
Webster, B. and Williamson, G., ‘A geometric model for Hochschild homology of Soergel bimodules’, Geom. Topol. 12(2), (2008), 1243–1263.CrossRefGoogle Scholar