Hostname: page-component-669899f699-vbsjw Total loading time: 0 Render date: 2025-04-27T13:52:33.952Z Has data issue: false hasContentIssue false
  • English
  • Français

SPLITTING INVARIANT SUBSPACES IN THE HARDY SPACE OVER THE BIDISK

Part of: Special classes of linear operators General theory of linear operators Holomorphic functions of several complex variables

Published online by Cambridge University Press:  12 May 2016

KEI JI IZUCHI ,
KOU HEI IZUCHI  and
YUKO IZUCHI
KEI JI IZUCHI*
Affiliation:
Department of Mathematics, Niigata University, Niigata 950-2181, Japan email [email protected]
KOU HEI IZUCHI
Affiliation:
Department of Mathematics, Faculty of Education, Yamaguchi University, Yamaguchi 753-8511, Japan email [email protected]
YUKO IZUCHI
Affiliation:
Aoyama-shinmachi 18-6-301, Nishi-ku, Niigata 950-2006, Japan email [email protected]
*
✉[email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 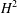$H^{2}$ be the Hardy space over the bidisk. It is known that Hilbert–Schmidt invariant subspaces of 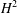$H^{2}$ have nice properties. An invariant subspace which is unitarily equivalent to some invariant subspace whose continuous spectrum does not coincide with 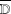$\overline{\mathbb{D}}$ is Hilbert–Schmidt. We shall introduce the concept of splittingness for invariant subspaces and prove that they are Hilbert–Schmidt.

Keywords

Hardy space over the bidisksplitting invariant subspaceHilbert–Schmidt invariant subspaceRudin type invariant subspace

MSC classification

Primary: 47A15: Invariant subspaces
Secondary: 32A35: $H^p$-spaces, Nevanlinna spaces 47B35: Toeplitz operators, Hankel operators, Wiener-Hopf operators
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 102 , Issue 2 , April 2017 , pp. 205 - 223
Copyright
© 2016 Australian Mathematical Publishing Association Inc. 

Footnotes

The first author is partially supported by Grant-in-Aid for Scientific Research, Japan Society for the Promotion of Science (no. 24540164).

References

Agrawal, O., Clark, D. and Douglas, R., ‘Invariant subspaces in the polydisk’, Pacific J. Math. 121 (1986), 1–11.Google Scholar
Bercovici, H., ‘Operator theory and arithmetic in H ∞ ’, in: Mathematical Surveys and Monographs, Vol. 26 (American Mathematical Society, Providence, RI, 1988).Google Scholar
Chen, X. and Guo, K., Analytic Hilbert Modules (Chapman & Hall/CRC, Boca Raton, FL, 2003).Google Scholar
Douglas, R. and Yang, R., ‘Operator theory in the Hardy space over the bidisk I’, Integral Equ. Operator Theory 38 (2000), 207–221.Google Scholar
Guo, K. and Yang, R., ‘The core function of submodules over the bidisk’, Indiana Univ. Math. J. 53 (2004), 205–222.Google Scholar
Hoffman, K., Banach Spaces of Analytic Functions (Prentice Hall, Englewood Cliffs, NJ, 1962).Google Scholar
Izuchi, K. J. and Izuchi, K. H., ‘Rank-one commutators on invariant subspaces of the Hardy space on the bidisk’, J. Operator Theory 60 (2008), 239–251.Google Scholar
Izuchi, K. J., Izuchi, K. H. and Izuchi, Y., ‘Blaschke products and the rank of backward shift invariant subspaces over the bidisk’, J. Funct. Anal. 261 (2011), 1457–1468.Google Scholar
Izuchi, K. J., Izuchi, K. H. and Izuchi, Y., ‘Ranks of invariant subspaces of the Hardy space over the bidisk’, J. reine angew. Math. 659 (2011), 67–100.Google Scholar
Izuchi, K. J., Izuchi, K. H. and Izuchi, Y., ‘Ranks of backward shift invariant subspaces of the Hardy space over the bidisk’, Math. Z. 274 (2013), 885–903.CrossRefGoogle Scholar
Izuchi, K. J., Nakazi, T. and Seto, M., ‘Backward shift invariant subspaces in the bidisc II’, J. Operator Theory 51 (2004), 361–375.Google Scholar
Mandreckar, V., ‘The validity of Beurling theorems in polydiscs’, Proc. Amer. Math. Soc. 103 (1988), 145–148.CrossRefGoogle Scholar
Nikol’skiǐ, N., Treatise on the Shift Operator (Springer, New York, 1986).Google Scholar
Rudin, W., Function Theory in Polydiscs (Benjamin, New York, 1969).Google Scholar
Seto, M., ‘Infinite sequences of inner functions and submodules in H 2(D 2)’, J. Operator Theory 61 (2009), 75–86.Google Scholar
Seto, M. and Yang, R., ‘Inner sequence based invariant subspaces in H 2(D 2)’, Proc. Amer. Math. Soc. 135 (2007), 2519–2526.Google Scholar
Sz.-Nagy, B. and Foiaş, C., Harmonic Analysis of Operators on Hilbert Space (North Holland, Amsterdam, 1970).Google Scholar
Yang, R., ‘The Berger–Shaw theorem in the Hardy module over the bidisk’, J. Operator Theory 42 (1999), 379–404.Google Scholar
Yang, R., ‘Operator theory in the Hardy space over the bidisk (III)’, J. Funct. Anal. 186 (2001), 521–545.CrossRefGoogle Scholar
Yang, R., ‘Beurling’s phenomenon in two variables’, Integral Equ. Operator Theory 48 (2004), 411–423.Google Scholar
Yang, R., ‘The core operator and congruent submodules’, J. Funct. Anal. 228 (2005), 469–489.Google Scholar
Yang, R., ‘Hilbert–Schmidt submodules and issues of unitary equivalence’, J. Operator Theory 53 (2005), 169–184.Google Scholar
Yang, R., ‘On two variable Jordan block II’, Integral Equ. Operator Theory 56 (2006), 431–449.Google Scholar
Yang, Y., ‘Two inner sequences based invariant subspaces in H 2(D2)’, Integral Equ. Operator Theory 77 (2013), 279–290.Google Scholar