Hostname: page-component-669899f699-swprf Total loading time: 0 Render date: 2025-04-27T16:59:30.490Z Has data issue: false hasContentIssue false
  • English
  • Français

On indefinite ternary quadratic forms

Published online by Cambridge University Press:  09 April 2009

R. T. Worley
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In a paper [1] with the same title Barnes has shown that if Q(x, y, z) is an indefinite ternary quadratic form of determinant d ≠ 0 then there exist integers x1, y1, z1, x2,···z3 satisfying for which 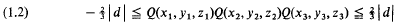Furthermore, unless Q is equivalent to a multiple of 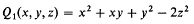or two other forms Q2, Q3 then the constant ⅔ in (1.2) can be replaced by 1/2.2. For Q1 equality is needed on at least one side of (1.2) while for Q2, Q3 the constant ⅔ can be reduced to 12/25 but no further.

Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 18 , Issue 4 , December 1974 , pp. 388 - 401
Copyright
Copyright © Australian Mathematical Society 1974

References

[1]Barnes, E. S., ‘On Indefinite Ternary Quadratic forms’, Proc. Lond. Math. Soc. (3) 2 (1952), 218–233.CrossRefGoogle Scholar
[2]Barnes, E. S., ‘The Minimum of the Product of two Values of a Quadratic Form III’, Proc. Lond. Math. Soc. (3) 1 (1951), 415–434.CrossRefGoogle Scholar
[3]Dickson, L. E., Studies in the Theory of Numbers, Chicago (1930).Google Scholar
[4]Blaney, H., ‘Indefinite Quadratic Forms in n Variables’, J. Lond. Math. Soc. 23 (1948), 153–160.CrossRefGoogle Scholar
[5]Oppenheim, A., ‘Values of Quadratic Forms’, Quart. J. Math. (Ox.) (2) 4 (1953), 54–59.CrossRefGoogle Scholar
[6]Worley, R. T., ‘Asymmetric Minima of Indefinite Ternary Quadratic Forms’, J. Austral. Math. Soc. 7 (1967), 191–238.CrossRefGoogle Scholar