Hostname: page-component-669899f699-cf6xr Total loading time: 0 Render date: 2025-05-01T13:52:41.038Z Has data issue: false hasContentIssue false
  • English
  • Français

ON FREE SPECTRA OF A CLASS OF FINITE INVERSE MONOIDS

Part of: Varieties Semigroups

Published online by Cambridge University Press:  07 March 2013

IGOR DOLINKA
IGOR DOLINKA*
Affiliation:
Department of Mathematics and Informatics, University of Novi Sad, Trg Dositeja Obradovića 4, 21101 Novi Sad, Serbia email [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

For a finite Clifford inverse algebra 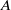$A$, with natural order meet-semilattice 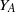${Y}_{A} $ and group of units 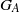${G}_{A} $, we show that the inverse monoid obtained as the semidirect product 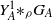${ Y}_{A}^{1} {\mathop{\ast }\nolimits}_{\rho } {G}_{A} $ has a log-polynomial free spectrum whenever 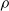$\rho $ is a term-expressible left action of 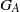${G}_{A} $ on 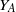${Y}_{A} $ and all subgroups of 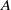$A$ are nilpotent. This yields a number of examples of finite inverse monoids satisfying the Seif conjecture on finite monoids whose free spectra are not doubly exponential.

Keywords

free spectrumfinite inverse monoidsemidirect productClifford inverse algebra

MSC classification

Secondary: 20M05: Free semigroups, generators and relations, word problems 20M18: Inverse semigroups 08B20: Free algebras
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 93 , Issue 3 , December 2012 , pp. 225 - 237
Copyright
Copyright ©2013 Australian Mathematical Publishing Association Inc. 

References

Berman, J., ‘Free spectra gaps and tame congruence types’, Internat. J. Algebra Comput. 5 (1995), 651–672.CrossRefGoogle Scholar
Berman, J. and Idziak, P. M., Generative Complexity in Algebra, Memoirs of the American Mathematical Society, 175 (American Mathematical Society, Providence, RI, 2005), No. 828.CrossRefGoogle Scholar
Burris, S. and Sankappanavar, H. P., A Course in Universal Algebra (Springer, New York, 1981).CrossRefGoogle Scholar
Crvenković, S. and Ruškuc, N., ‘Log-linear varieties of semigroups’, Algebra Universalis 33 (1995), 470–474.CrossRefGoogle Scholar
Dolinka, I., ‘On free spectra of completely regular semigroups and monoids’, J. Pure Appl. Algebra 213 (2009), 1979–1990.CrossRefGoogle Scholar
Dolinka, I., ‘On free spectra of locally testable semigroup varieties’, Glasg. Math. J. 53 (2011), 623–629.CrossRefGoogle Scholar
Dolinka, I., ‘On free spectra of finite monoids from the pseudovariety DA’, Semigroup Forum 85 (2012), 244–254.CrossRefGoogle Scholar
Dombi, E. R. and Ruškuc, N., ‘On generators and presentations of semidirect products in inverse semigroups’, Bull. Aust. Math. Soc. 79 (2009), 353–365.CrossRefGoogle Scholar
Grätzer, G. and Kisielewicz, A., ‘A survey of some open problems on ${p}_{n} $-sequences and free spectra of algebras and varieties’, in: Universal Algebra and Quasigroup Theory (Jadwisin, 1989) (Heldermann, Berlin, 1992), 57–88.Google Scholar
Higman, G., ‘The orders of relatively free groups’, in: Proc. Internat. Conf. Theory of Groups (Canberra, 1965) (Gordon & Breach, New York, 1967), 153–165.Google Scholar
Hobby, D. and McKenzie, R., The Structure of Finite Algebras, Contemporary Mathematics, 76 (American Mathematical Society, Providence, RI, 1988).CrossRefGoogle Scholar
Jackson, M., ‘Flat algebras and the translation of universal Horn logic to equational logic’, J. Symbolic Logic 73 (2008), 90–128.CrossRefGoogle Scholar
Jackson, M. and Stokes, T., ‘Agreeable semigroups’, J. Algebra 266 (2003), 393–417.CrossRefGoogle Scholar
Kátai-Urbán, K. and Szabó, Cs., ‘Free spectrum of the variety generated by the five element combinatorial Brandt semigroup’, Semigroup Forum 73 (2006), 253–260.CrossRefGoogle Scholar
Kátai-Urbán, K. and Szabó, Cs., ‘On the free spectrum of the variety generated by the combinatorial completely 0-simple semigroups’, Glasg. Math. J. 49 (2007), 93–98.CrossRefGoogle Scholar
Kearnes, K. A., ‘Congruence modular varieties with small free spectra’, Algebra Universalis 42 (1999), 165–181.CrossRefGoogle Scholar
Kitaev, S. and Seif, S. W., ‘Word problem of the Perkins semigroup via directed acyclic graphs’, Order 25 (2008), 177–194.CrossRefGoogle Scholar
Lawson, M. V., Inverse Semigroups: The Theory of Partial Symmetries (World Scientific, River Edge, NJ, 1998).CrossRefGoogle Scholar
Leech, J., ‘Inverse monoids with a natural semilattice ordering’, Proc. London Math. Soc. (3) 70 (1995), 146–182.CrossRefGoogle Scholar
Neumann, P., ‘Some indecomposable varieties of groups’, Quart. J. Math. Oxford (2) 14 (1965), 46–50.CrossRefGoogle Scholar
Reilly, N. R., ‘Minimal noncryptic varieties of inverse semigroups’, Quart. J. Math. Oxford (2) 36 (1985), 467–487.CrossRefGoogle Scholar
Reilly, N. R., ‘Large varieties generated by small inverse semigroups’, Acta Sci. Math. (Szeged) 58 (1993), 25–41.Google Scholar
Sapir, M. V., ‘Identities of finite inverse semigroups’, Internat. J. Algebra Comput. 3 (1993), 115–124.CrossRefGoogle Scholar
Seif, S. W., ‘Monoids with sub-log-exponential free spectra’, J. Pure Appl. Algebra 212 (2008), 1162–1174.CrossRefGoogle Scholar