 $1/\unicode[STIX]{x1D70B}$
$1/\unicode[STIX]{x1D70B}$Published online by Cambridge University Press: 01 February 2019
In this article, we give new proofs of two of Ramanujan’s 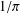 $1/\unicode[STIX]{x1D70B}$ formulae and
$1/\unicode[STIX]{x1D70B}$ formulae and 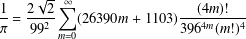 $$\begin{eqnarray}\frac{1}{\unicode[STIX]{x1D70B}}=\frac{2\sqrt{2}}{99^{2}}\mathop{\sum }_{m=0}^{\infty }(26390m+1103)\frac{(4m)!}{396^{4m}(m!)^{4}}\end{eqnarray}$$ using the theory of modular forms. The method can also be used to prove other classical
$$\begin{eqnarray}\frac{1}{\unicode[STIX]{x1D70B}}=\frac{2\sqrt{2}}{99^{2}}\mathop{\sum }_{m=0}^{\infty }(26390m+1103)\frac{(4m)!}{396^{4m}(m!)^{4}}\end{eqnarray}$$ using the theory of modular forms. The method can also be used to prove other classical 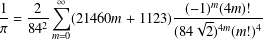 $$\begin{eqnarray}\frac{1}{\unicode[STIX]{x1D70B}}=\frac{2}{84^{2}}\mathop{\sum }_{m=0}^{\infty }(21460m+1123)\frac{(-1)^{m}(4m)!}{(84\sqrt{2})^{4m}(m!)^{4}}\end{eqnarray}$$
$$\begin{eqnarray}\frac{1}{\unicode[STIX]{x1D70B}}=\frac{2}{84^{2}}\mathop{\sum }_{m=0}^{\infty }(21460m+1123)\frac{(-1)^{m}(4m)!}{(84\sqrt{2})^{4m}(m!)^{4}}\end{eqnarray}$$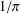 $1/\unicode[STIX]{x1D70B}$ formulae.
$1/\unicode[STIX]{x1D70B}$ formulae.