Hostname: page-component-669899f699-rg895 Total loading time: 0 Render date: 2025-04-29T17:42:08.262Z Has data issue: false hasContentIssue false
  • English
  • Français

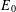MEASURABLE $E_{0}$-SEMIGROUPS ARE CONTINUOUS

Part of: Selfadjoint operator algebras

Published online by Cambridge University Press:  04 December 2019

S. P. MURUGAN
S. P. MURUGAN*
Affiliation:
Indian Institute of Science Education and Research, Mohali, India e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 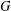$G$ be a second countable locally compact Hausdorff topological group and 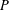$P$ be a closed subsemigroup of 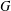$G$ containing the identity element 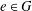$e\in G$. Assume that the interior of 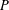$P$ is dense in 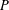$P$. Let 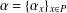$\unicode[STIX]{x1D6FC}=\{{\unicode[STIX]{x1D6FC}_{x}\}}_{x\in P}$ be a semigroup of unital normal $\ast$-endomorphisms of a von Neumann algebra 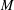$M$ with separable predual satisfying a natural measurability hypothesis. We show that $\unicode[STIX]{x1D6FC}$ is an 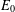$E_{0}$-semigroup over 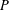$P$ on 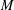$M$.

Keywords

E0-semigroupsvon Neumann algebranormal *-homomorphismOre semigroup

MSC classification

Primary: 46L55: Noncommutative dynamical systems
Secondary: 46L99: None of the above, but in this section
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 111 , Issue 2 , October 2021 , pp. 278 - 288
Check for updates
Copyright
© 2019 Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

Footnotes

Communicated by A. Sims

References

Anbu, A., Srinivasan, R. and Sundar, S., ‘E-semigroups over closed convex cones’, Preprint, 2018, arXiv:1807.11375.Google Scholar
Anbu, A. and Sundar, S., ‘ $CCR$ flows associated to closed convex cones’, Münster J. Math. 2018, to appear.Google Scholar
Arveson, W., ‘Continuous analogues of Fock space’, Mem. Amer. Math. Soc. 80(409) (1989), iv+66.Google Scholar
Arveson, W., ‘Continuous analogues of Fock space. III. Singular states’, J. Operator Theory 22(1) (1989), 165–205.Google Scholar
Arveson, W., ‘Continuous analogues of Fock space. II. The spectral C ∗ -algebra’, J. Funct. Anal. 90(1) (1990), 138–205.CrossRefGoogle Scholar
Arveson, W., ‘Continuous analogues of Fock space. IV. Essential states’, Acta Math. 164(3–4) (1990), 265–300.CrossRefGoogle Scholar
Arveson, W., Noncommutative Dynamics and E-semigroups, Springer Monographs in Mathematics (Springer, New York, 2003).CrossRefGoogle Scholar
Hilgert, J. and Neeb, K.-H., ‘Wiener–Hopf operators on ordered homogeneous spaces. I’, J. Funct. Anal. 132(1) (1995), 86–118.CrossRefGoogle Scholar
Hille, E. and Phillips, R. S., Functional Analysis and Semi-Groups, Part 1, American Mathematical Society Colloquium Publications, 31 (American Mathematical Society, Providence, RI, 1996).Google Scholar
Izumi, M. and Srinivasan, R., ‘Generalized CCR flows’, Comm. Math. Phys. 281(2) (2008), 529–571.CrossRefGoogle Scholar
Izumi, M. and Srinivasan, R., ‘Toeplitz CAR flows and type I factorizations’, Kyoto J. Math. 50(1) (2010), 1–32.CrossRefGoogle Scholar
Murugan, S. P. and Sundar, S., ‘ $E_{0}^{P}$ -semigroups and product systems’, Preprint, 2017,arXiv:1706.03928.Google Scholar
Murugan, S. P. and Sundar, S., ‘On the existence of E 0 -semigroups – the multiparameter case’, Infin. Dimens. Anal. Quantum Probab. Relat. Top. 21(2) (2018), 20 pages.CrossRefGoogle Scholar
Parthasarathy, K. R., An Introduction to Quantum Stochastic Calculus, Monographs in Mathematics, 85 (Birkhäuser–Springer, Basel, 1992).Google Scholar
Powers, R. T., ‘A nonspatial continuous semigroup of ∗-endomorphisms of 𝓑(𝓗)’, Publ. Res. Inst. Math. Sci. 23(6) (1987), 1053–1069.CrossRefGoogle Scholar
Powers, R. T., ‘An index theory for semigroups of ∗ -endomorphisms of 𝓑(𝓗) and type II 1 factors’, Canad. J. Math. 40(1) (1988), 86–114.CrossRefGoogle Scholar
Powers, R. T., ‘On the structure of continuous spatial semigroups of ∗-endomorphisms of 𝓑(𝓗)’, Internat. J. Math. 2(3) (1991), 323–360.CrossRefGoogle Scholar
Renault, J. and Sundar, S., ‘Groupoids associated to Ore semigroup actions’, J. Operator Theory 73(2) (2015), 491–514.CrossRefGoogle Scholar
Shalit, O. M., ‘ E 0 -dilation of strongly commuting CP 0 -semigroups’, J. Funct. Anal. 255(1) (2008), 46–89.CrossRefGoogle Scholar
Shalit, O. M., ‘What type of dynamics arise in E 0 -dilations of commuting quantum Markov semigroups?’, Infin. Dimens. Anal. Quantum Probab. Relat. Top. 11(3) (2008), 393–403.CrossRefGoogle Scholar
Shalit, O. M., ‘E-dilation of strongly commuting CP-semigroups (the nonunital case)’, Houston J. Math. 37(1) (2011), 203–232.Google Scholar
Tsirelson, B., ‘Non-isomorphic product systems’, in: Advances in Quantum Dynamics (South Hadley, MA, 2002), Contemporary Mathematics, 335 (American Mathematical Society, Providence, RI, 2003), 273–328.CrossRefGoogle Scholar