Hostname: page-component-669899f699-chc8l Total loading time: 0 Render date: 2025-04-29T11:36:15.544Z Has data issue: false hasContentIssue false
  • English
  • Français

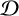FINITELY PRESENTED INVERSE SEMIGROUPS WITH FINITELY MANY IDEMPOTENTS IN EACH $\mathcal D$-CLASS AND NON-HAUSDORFF UNIVERSAL GROUPOIDS

Part of: Topological and differentiable algebraic systems Semigroups

Published online by Cambridge University Press:  13 December 2023

PEDRO V. SILVA  and
BENJAMIN STEINBERG Open the ORCID record for BENJAMIN STEINBERG [Opens in a new window]
PEDRO V. SILVA
Affiliation:
Centro de Matemática, Faculdade de Ciências, Universidade do Porto, R. Campo Alegre 687, 4169-007 Porto, Portugal e-mail: [email protected]
BENJAMIN STEINBERG*
Affiliation:
Department of Mathematics, City College of New York, Convent Avenue at 138th Street, New York, New York 10031, USA
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The complex algebra of an inverse semigroup with finitely many idempotents in each 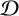$\mathcal D$-class is stably finite by a result of Munn. This can be proved fairly easily using 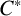$C^{*}$-algebras for inverse semigroups satisfying this condition that have a Hausdorff universal groupoid, or more generally for direct limits of inverse semigroups satisfying this condition and having Hausdorff universal groupoids. It is not difficult to see that a finitely presented inverse semigroup with a non-Hausdorff universal groupoid cannot be a direct limit of inverse semigroups with Hausdorff universal groupoids. We construct here countably many nonisomorphic finitely presented inverse semigroups with finitely many idempotents in each $\mathcal D$-class and non-Hausdorff universal groupoids. At this time, there is not a clear 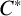$C^{*}$-algebraic technique to prove these inverse semigroups have stably finite complex algebras.

Keywords

inverse monoidsample groupoidsnon-Hausdorff groupoids

MSC classification

Primary: 20M18: Inverse semigroups
Secondary: 20M05: Free semigroups, generators and relations, word problems 22A22: Topological groupoids (including differentiable and Lie groupoids)
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 116 , Issue 3 , June 2024 , pp. 384 - 398
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

Footnotes

Communicated by Lisa Orloff Clark

The first author acknowledges support from the Center of Mathematics of the University of Porto, which is financed by national funds through the Fundação para a Ciência e a Tecnologia, I.P., under the project with reference UIDB/00144/2020. The second author was supported by a PSC CUNY grant and a Simons Foundation Collaboration Grant, award number 849561.

References

Bartholdi, L. and Silva, P. V., ‘Rational subsets of groups’, in: Handbook of Automata Theory (ed. Pin, J.-E.) (EMS Press, Berlin, 2021), Ch. 23.Google Scholar
Lawson, M. V., Inverse Semigroups: The Theory of Partial Symmetries (World Scientific, River Edge, NJ, 1998).CrossRefGoogle Scholar
Munn, W. D., ‘Free inverse semigroups’, Proc. Lond. Math. Soc. (3) 29(3) (1974), 385–404.CrossRefGoogle Scholar
Munn, W. D., ‘Direct finiteness of certain monoid algebras. I’, Proc. Edinb. Math. Soc. (2) 39(2) (1996), 365–369; II, 371–376.CrossRefGoogle Scholar
Paterson, A. L. T., Groupoids, Inverse Semigroups, and their Operator Algebras, Progress in Mathematics, 170 (Birkhäuser Boston Inc., Boston, MA, 1999).CrossRefGoogle Scholar
Sakarovitch, J., Elements of Automata Theory (Cambridge University Press, Cambridge, 2009).CrossRefGoogle Scholar
Scheiblich, H. E., ‘Free inverse semigroups’, Proc. Amer. Math. Soc. 38 (1973), 1–7.CrossRefGoogle Scholar
Steinberg, B., ‘A groupoid approach to discrete inverse semigroup algebras’, Adv. Math. 223(2) (2010), 689–727.CrossRefGoogle Scholar
Steinberg, B., ‘Stable finiteness of ample groupoid algebras, traces and applications’, Preprint, 2022, arXiv:2207.11194.Google Scholar
Stephen, J. B., ‘Presentations of inverse monoids’, J. Pure Appl. Algebra 63 (1990), 81–112.CrossRefGoogle Scholar