Hostname: page-component-669899f699-2mbcq Total loading time: 0 Render date: 2025-04-27T22:47:45.789Z Has data issue: false hasContentIssue false
  • English
  • Français

FINITELY CONSTRAINED GROUPS OF MAXIMAL HAUSDORFF DIMENSION

Part of: Topological dynamics Compact groups Structure and classification of infinite or finite groups

Published online by Cambridge University Press:  11 November 2015

ANDREW PENLAND  and
ZORAN ŠUNIĆ
ANDREW PENLAND*
Affiliation:
Department of Mathematics, Texas A&M University, College Station, TX 77843-3368, USA email [email protected]
ZORAN ŠUNIĆ
Affiliation:
Department of Mathematics, Texas A&M University, College Station, TX 77843-3368, USA email [email protected]
*
✉[email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We prove that if 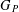$G_{P}$ is a finitely constrained group of binary rooted tree automorphisms (a group binary tree subshift of finite type) defined by an essential pattern group 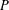$P$ of pattern size 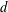$d$, 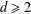$d\geq 2$, and if 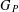$G_{P}$ has maximal Hausdorff dimension (equal to 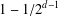$1-1/2^{d-1}$), then 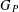$G_{P}$ is not topologically finitely generated. We describe precisely all essential pattern groups 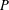$P$ that yield finitely constrained groups with maximal Hausdorff dimension. For a given size 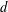$d$, 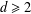$d\geq 2$, there are exactly 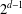$2^{d-1}$ such pattern groups and they are all maximal in the group of automorphisms of the finite rooted regular tree of depth 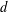$d$.

Keywords

finitely constrained groupsgroups acting on treessymbolic dynamics on treesgroup tree shiftsHausdorff dimension

MSC classification

Primary: 20E08: Groups acting on trees
Secondary: 22C05: Compact groups 37B10: Symbolic dynamics 37B99: None of the above, but in this section
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 100 , Issue 1 , February 2016 , pp. 108 - 123
Copyright
© 2015 Australian Mathematical Publishing Association Inc. 

References

Abercrombie, A. G., ‘Subgroups and subrings of profinite rings’, Math. Proc. Cambridge Philos. Soc. 116(2) (1994), 209–222.CrossRefGoogle Scholar
Abért, M. and Virág, B., ‘Dimension and randomness in groups acting on rooted trees’, J. Amer. Math. Soc. 18(1) (2005), 157–192.CrossRefGoogle Scholar
Aubrun, N. and Béal, M., ‘Tree-shifts of finite type’, Theoret. Comput. Sci. 459 (2012), 16–25.CrossRefGoogle Scholar
Barnea, Y. and Shalev, A., ‘‘Hausdorff dimension, pro-p groups, and Kac–Moody algebras’’, Trans. Amer. Math. Soc. 349 (1997), 5073–5091.CrossRefGoogle Scholar
Bartholdi, L., ‘Branch rings, thinned rings, tree enveloping rings’, Israel J. Math. (2006), 93–139.CrossRefGoogle Scholar
Bartholdi, L. and Nekrashevych, V., ‘Iterated monodromy groups of quadratic polynomials, I’, Groups Geom. Dyn. 2 (2008), 309–336.CrossRefGoogle Scholar
Bartholdi, L. and Šuniḱ, Z., ‘On the word and period growth of some groups of tree automorphisms’, Comm. Algebra 29(11) (2001), 4923–4964.CrossRefGoogle Scholar
Bondarenko, I., Grigorchuk, R., Kravchenko, R., Muntyan, Y., Nekrashevych, V., Savchuk, D. and Šunić, Z., ‘On classification of groups generated by 3-state automata over a 2-letter alphabet’, Algebra Discrete Math. (1) (2008), 1–163.Google Scholar
Bondarenko, I. V. and Samoilovych, I. O., ‘On finite generation of self-similar groups of finite type’, Internat. J. Algebra Comput. 23(1) (2013), 69–79.CrossRefGoogle Scholar
Ceccherini-Silberstein, T., Coornaert, M., Fiorenzi, F. and Šunić, Z., ‘Cellular automata between sofic tree shifts’, Theoret. Comput. Sci. 506 (2013), 79–101.CrossRefGoogle Scholar
Grigorchuk, R., ‘Just infinite branch groups’, in: New Horizons in Pro-p Groups (eds. du Sautoy, M., Egal, D. and Shalev, A.) (Birkhäuser, Boston, 2000), 121–179.CrossRefGoogle Scholar
Grigorchuk, R., ‘Solved and unsolved problems around one group’, in: Infinite Groups: Geometric, Combinatorial and Dynamical Aspects, Progress in Mathematics, 248 (Birkhäuser, Basel, 2005), 117–218.CrossRefGoogle Scholar
Pink, R., ‘Profinite iterated monodromy groups arising from quadratic polynomials’, Preprint, 2013, arXiv:1307.5678v3.Google Scholar
Siegenthaler, O., ‘Hausdorff dimension of some groups acting on the binary tree’, J. Group Theory 11(4) (2008), 555–567.CrossRefGoogle Scholar
Šunić, Z., ‘Hausdorff dimension in a family of self-similar groups’, Geom. Dedicata 124(1) (2007), 213–236.CrossRefGoogle Scholar
Šunić, Z., ‘Pattern closure in groups of tree automorphisms’, Bull. Math. Sci. 1(1) (2011), 115–127.CrossRefGoogle Scholar