Hostname: page-component-669899f699-7tmb6 Total loading time: 0 Render date: 2025-04-26T18:51:02.692Z Has data issue: false hasContentIssue false
  • English
  • Français

CLASS GROUP STATISTICS FOR TORSION FIELDS GENERATED BY ELLIPTIC CURVES

Part of: Algebraic number theory: global fields Arithmetic algebraic geometry

Published online by Cambridge University Press:  02 December 2024

ANWESH RAY Open the ORCID record for ANWESH RAY [Opens in a new window]  and
TOM WESTON Open the ORCID record for TOM WESTON [Opens in a new window]
ANWESH RAY*
Affiliation:
Chennai Mathematical Institute, H1, SIPCOT IT Park, Kelambakkam, Siruseri, Tamil Nadu 603103, India
TOM WESTON
Affiliation:
Department of Mathematics, University of Massachusetts, Amherst, MA, USA e-mail: [email protected]
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

For a prime p and a rational elliptic curve 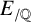$E_{/\mathbb {Q}}$, set 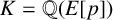$K=\mathbb {Q}(E[p])$ to denote the torsion field generated by 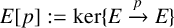$E[p]:=\operatorname {ker}\{E\xrightarrow {p} E\}$. The class group 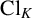$\operatorname {Cl}_K$ is a module over 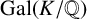$\operatorname {Gal}(K/\mathbb {Q})$. Given a fixed odd prime number p, we study the average nonvanishing of certain Galois stable quotients of the mod-p class group 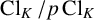$\operatorname {Cl}_K/p\operatorname {Cl}_K$. Here, E varies over all rational elliptic curves, ordered according to height. Our results are conditional, since we assume that the p-primary part of the Tate–Shafarevich group is finite. Furthermore, we assume predictions made by Delaunay for the statistical variation of the p-primary parts of Tate–Shafarevich groups. We also prove results in the case when the elliptic curve 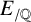$E_{/\mathbb {Q}}$ is fixed and the prime p is allowed to vary.

Keywords

torsion fieldsclass groupsSelmer groups of elliptic curvesarithmetic statistics

MSC classification

Primary: 11G05: Elliptic curves over global fields
Secondary: 11R29: Class numbers, class groups, discriminants 11R32: Galois theory 11R34: Galois cohomology 11R45: Density theorems
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 118 , Issue 2 , April 2025 , pp. 245 - 264
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

Footnotes

Communicated by Michael Coons

From September 2022 to September 2023, the first author’s research is supported by the CRM Simons postdoctoral fellowship.

References

Bhargava, M., ‘The density of discriminants of quartic rings and fields’, Ann. of Math. (2) 162 (2005), 1031–1063.CrossRefGoogle Scholar
Cohen, H. and Lenstra, H. W., ‘Heuristics on class groups of number fields’, in: Number Theory Noordwijkerhout 1983 (ed. Jager, H.) (Springer, Berlin–Heidelberg, 1984), 33–62.CrossRefGoogle Scholar
Coates, J. H. and Sujatha, R., Galois Cohomology of Elliptic Curves, Lecture Notes at the Tata Institute of Fundamental Research, 88 (Narosa, New Delhi, 2000).Google Scholar
Cremona, J. E. and Sadek, M., ‘Local and global densities for Weierstrass models of elliptic curves’, Math. Res. Lett. 30(2) (2023), 413–461.CrossRefGoogle Scholar
Delaunay, C., ‘Heuristics on class groups and on Tate–Shafarevich groups: the magic of the Cohen–Lenstra heuristics’, in Ranks of Elliptic Curves and Random Matrix Theory, London Mathematical Society Lecture Note Series, 341 (eds. Conrey, J. B., Farmer, D. W., Mezzadri, F. and Snaith, N. C.) (Cambridge University Press, Cambridge, 2007), 323–340.CrossRefGoogle Scholar
Davenport, H. and Heilbronn, H. A., ‘On the density of discriminants of cubic fields. II’, Proc. Roy. Soc. Lond. A 322(1551) (1971), 405–420.Google Scholar
Duke, W., ‘Elliptic curves with no exceptional primes’, C. R. Acad. Sci. Sér. 1 325(8) (1997), 813–818.Google Scholar
Ellenberg, J., Pierce, L. and Wood, M., ‘On $\ell$ -torsion in class groups of number fields’, Algebra Number Theory 11(8) (2017), 1739–1778.Google Scholar
Ellenberg, J. S. and Venkatesh, A., ‘Reflection principles and bounds for class group torsion’, Int. Math. Res. Not. IMRN 2007 (2007), Article no. 002.CrossRefGoogle Scholar
Fouvry, É. and Klüners, J., ‘On the 4-rank of class groups of quadratic number fields’, Invent. Math. 167(3) (2007), 455–513.Google Scholar
Lecouturier, E., ‘On the Galois structure of the class group of certain Kummer extensions’, J. Lond. Math. Soc. (2) 98(1) (2018), 35–58.Google Scholar
Lenstra, H. W. Jr, ‘Factoring integers with elliptic curves’, Ann. of Math. (2) 126 (1987), 649–673.CrossRefGoogle Scholar
Mazur, B., ‘Modular curves and the Eisenstein ideal’, Publ. Math. Inst. Hautes Études Sci. 47 (1978), 33–186; 1977. With an appendix by Mazur and M. Rapoport.CrossRefGoogle Scholar
Martinet, J. and Cohen, H., ‘Étude heuristique des groupes de classes des corps de nombres’, J. reine angew. Math., 404 (1990), 455–513.Google Scholar
Murty, V. K., ‘Modular forms and the Chebotarev density theorem II’, in: Analytic Number Theory, London Mathematical Society Lecture Note Series, 247 (ed. Motohashi, Y.) (Cambridge University Press, Cambridge, 1997), 287–308.CrossRefGoogle Scholar
Prasad, D. and Shekhar, S., ‘Relating the Tate–Shafarevich group of an elliptic curve with the class group’, Pacific J. Math. 312(1) (2021), 203–218.CrossRefGoogle Scholar
Ray, A. and Sujatha, R., ‘Arithmetic statistics for the fine Selmer group in Iwasawa theory’, Res. Number Theory 9(3) (2023), Paper no. 59, 25 pages.CrossRefGoogle Scholar
Schoof, R., ‘Nonsingular plane cubic curves over finite fields’, J. Combin. Theory Ser. A 46(2) (1987), 183–211.CrossRefGoogle Scholar
Silverman, J. H., Advanced Topics in the Arithmetic of Elliptic Curves, Graduate Texts in Mathematics, 151 (Springer-Verlag, New York, 1994).Google Scholar
Silverman, J. H., The Arithmetic of Elliptic Curves, 2nd edn, Graduate Texts in Mathematics, 106 (Springer, Dordrecht, 2009).CrossRefGoogle Scholar
Schaefer, K. and Stubley, E., ‘Class groups of Kummer extensions via cup products in Galois cohomology’, Trans. Amer. Math. Soc. 372(10) (2019), 6927–6980.CrossRefGoogle Scholar
Washington, L. C., Introduction to Cyclotomic Fields, 2nd edn, Graduate Texts in Mathematics, 83 (Springer-Verlag, New York, 1997).CrossRefGoogle Scholar
Watkins, M., ‘Class numbers of imaginary quadratic fields’, Math. Comp. 73(246) (2004), 907–938.CrossRefGoogle Scholar
Wong, S., ‘On the rank of ideal class groups’, in: Number Theory: Fifth Conference of the Canadian Number Theory Association, CRM Proceedings and Lecture Notes, 19 (eds. Gupta, R. and Williams, K. J.) (American Mathematical Society, Providence, RI, 1999), 377–383.Google Scholar
Wood, M. M., ‘Asymptotics for number fields and class groups’, in: Directions in Number Theory, Association for Women in Mathematics Series, 3 (eds. Eischen, E. E., Long, L., Pries, R. and Stange, K. E.) (Springer, Cham, 2016), 291–339.CrossRefGoogle Scholar
Wake, P. and Wang-Erickson, C., ‘The rank of Mazur’s Eisenstein ideal’, Duke Math. J. 169(1) (2020), 31–115.Google Scholar
Zywina, D., ‘On the possible images of the mod $\ell$ representations associated to elliptic curves over $\mathbb{Q}$ ’, Preprint, 2015, arXiv:1508.07660.Google Scholar