Published online by Cambridge University Press: 25 November 2024
Let 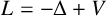 $L=-\Delta +V$ be a Schrödinger operator in
$L=-\Delta +V$ be a Schrödinger operator in 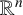 ${\mathbb R}^n$ with
${\mathbb R}^n$ with 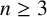 $n\geq 3$, where
$n\geq 3$, where 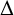 $\Delta $ is the Laplace operator denoted by
$\Delta $ is the Laplace operator denoted by 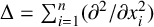 $\Delta =\sum ^{n}_{i=1}({\partial ^{2}}/{\partial x_{i}^{2}})$ and the nonnegative potential V belongs to the reverse Hölder class
$\Delta =\sum ^{n}_{i=1}({\partial ^{2}}/{\partial x_{i}^{2}})$ and the nonnegative potential V belongs to the reverse Hölder class  $(RH)_{q}$ with
$(RH)_{q}$ with 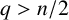 $q>n/2$. For
$q>n/2$. For 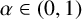 $\alpha \in (0,1)$, we define the operator
$\alpha \in (0,1)$, we define the operator 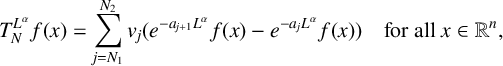 $$ \begin{align*} T_N^{L^{\alpha}} f(x) =\sum_{j=N_1}^{N_2} v_j(e^{-a_{j+1}L^\alpha} f(x)-e^{-a_{j}L^\alpha} f(x)) \quad \mbox{for all }x\in \mathbb R^n, \end{align*} $$
$$ \begin{align*} T_N^{L^{\alpha}} f(x) =\sum_{j=N_1}^{N_2} v_j(e^{-a_{j+1}L^\alpha} f(x)-e^{-a_{j}L^\alpha} f(x)) \quad \mbox{for all }x\in \mathbb R^n, \end{align*} $$
where 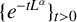 $\{e^{-tL^\alpha } \}_{t>0}$ is the fractional heat semigroup of the operator L,
$\{e^{-tL^\alpha } \}_{t>0}$ is the fractional heat semigroup of the operator L, 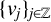 $\{v_j\}_{j\in \mathbb Z}$ is a bounded real sequence and
$\{v_j\}_{j\in \mathbb Z}$ is a bounded real sequence and 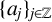 $\{a_j\}_{j\in \mathbb Z}$ is an increasing real sequence.
$\{a_j\}_{j\in \mathbb Z}$ is an increasing real sequence.
We investigate the boundedness of the operator 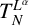 $T_N^{L^{\alpha }}$ and the related maximal operator
$T_N^{L^{\alpha }}$ and the related maximal operator 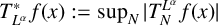 $T^*_{L^{\alpha }}f(x):=\sup _N \vert T_N^{L^{\alpha }} f(x)\vert $ on the spaces
$T^*_{L^{\alpha }}f(x):=\sup _N \vert T_N^{L^{\alpha }} f(x)\vert $ on the spaces 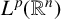 $L^{p}(\mathbb {R}^{n})$ and
$L^{p}(\mathbb {R}^{n})$ and 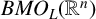 $BMO_{L}(\mathbb {R}^{n})$, respectively. As extensions of
$BMO_{L}(\mathbb {R}^{n})$, respectively. As extensions of 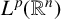 $L^{p}(\mathbb {R}^{n})$, the boundedness of the operators
$L^{p}(\mathbb {R}^{n})$, the boundedness of the operators 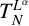 $T_N^{L^{\alpha }}$ and
$T_N^{L^{\alpha }}$ and 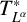 $T^*_{L^{\alpha }}$ on the Morrey space
$T^*_{L^{\alpha }}$ on the Morrey space 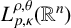 $L^{\rho ,\theta }_{p,\kappa }(\mathbb {R}^{n})$ and the weak Morrey space
$L^{\rho ,\theta }_{p,\kappa }(\mathbb {R}^{n})$ and the weak Morrey space 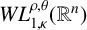 $WL^{\rho ,\theta }_{1,\kappa }(\mathbb {R}^{n})$ has also been proved.
$WL^{\rho ,\theta }_{1,\kappa }(\mathbb {R}^{n})$ has also been proved.
P.T. Li was supported by National Natural Science Foundation of China under grants (No. 12471093) and Shandong Natural Science Foundation of China (No. ZR2024MA016). Y. Liu was supported by National Natural Science Foundation of China (No. 12471089, No. 12271042), Beijing Natural Science Foundation of China (No. 1232023) and the National Science and Technology Major Project of China (No. J2019-I-0019-0018, No. J2019-I-0001-0001).
Communicated by Ji Li