Hostname: page-component-669899f699-ggqkh Total loading time: 0 Render date: 2025-05-03T23:48:44.837Z Has data issue: false hasContentIssue false
  • English
  • Français

BASIC NONARCHIMEDEAN JØRGENSEN THEORY

Part of: Structure and classification of infinite or finite groups

Published online by Cambridge University Press:  19 March 2024

MATTHEW CONDER Open the ORCID record for MATTHEW CONDER [Opens in a new window] ,
HARRIS LEUNG  and
JEROEN SCHILLEWAERT Open the ORCID record for JEROEN SCHILLEWAERT [Opens in a new window]
MATTHEW CONDER
Affiliation:
Department of Mathematics, University of Auckland, 38 Princes Street, Auckland 1010, New Zealand e-mail: [email protected]
HARRIS LEUNG
Affiliation:
Department of Mathematics, University of Auckland, 38 Princes Street, Auckland 1010, New Zealand e-mail: [email protected]
JEROEN SCHILLEWAERT*
Affiliation:
Department of Mathematics, University of Auckland, 38 Princes Street, Auckland 1010, New Zealand
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We prove a nonarchimedean analogue of Jørgensen’s inequality, and use it to deduce several algebraic convergence results. As an application, we show that every dense subgroup of 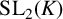${\mathrm {SL}_2}(K)$, where K is a p-adic field, contains two elements that generate a dense subgroup of 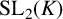${\mathrm {SL}_2}(K)$, which is a special case of a result by Breuillard and Gelander [‘On dense free subgroups of Lie groups’, J. Algebra 261(2) (2003), 448–467]. We also list several other related results, which are well known to experts, but not easy to locate in the literature; for example, we show that a nonelementary subgroup of 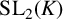${\mathrm {SL}_2}(K)$ over a nonarchimedean local field K is discrete if and only if each of its two-generator subgroups is discrete.

Keywords

Jørgensen’s inequalitydiscrete groupsBruhat–Tits treenonarchimedean local fields

MSC classification

Primary: 20E08: Groups acting on trees
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 117 , Issue 3 , December 2024 , pp. 273 - 287
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

Footnotes

Communicated by George Willis

The first and third author are supported by the New Zealand Marsden Fund. The first author is also supported by the Rutherford Foundation.

References

Armitage, J. V. and Parker, J. R., ‘Jørgensen’s inequality for non-archimedean metric spaces’, in: Geometry and Dynamics of Groups and Spaces (eds. Kapranov, M., Manin, Y. I., Moree, P., Kolyada, S. and Potyagailo, L.) (Birkhäuser, Basel, 2008), 97–111.CrossRefGoogle Scholar
Beardon, A., The Geometry of Discrete Groups, Graduate Texts in Mathematics, 91 (Springer-Verlag, New York, 1995).Google Scholar
Bourbaki, N., Elements of Mathematics: General Topology. Part 2 (Hermann, Paris, 1966).Google Scholar
Breuillard, E. and Gelander, T., ‘On dense free subgroups of Lie groups’, J. Algebra 261(2) (2003), 448–467.CrossRefGoogle Scholar
Bridson, M. and Haefliger, A., Metric Spaces of Non-Positive Curvature, Grundlehren der mathematischen Wissenschaften, 319 (Springer-Verlag, Berlin, 1999).CrossRefGoogle Scholar
Bruhat, F. and Tits, J., ‘Groupes réductifs sur un corps local. I. Données radicielles valuées’, Publ. Math. Inst. Hautes Études Sci. 41 (1972), 5–251.CrossRefGoogle Scholar
Caprace, P. E. and De Medts, T., ‘Simple locally compact groups acting on trees and their germs of automorphisms’, Transform. Groups 16(2) (2011), 375–411.CrossRefGoogle Scholar
Cassels, J. W. S., Local Fields (Cambridge University Press, Cambridge, 1986).CrossRefGoogle Scholar
Conder, M. J. and Schillewaert, J., ‘Discrete two-generator subgroups of $\mathrm{PSL}_2$ over non-archimedean local fields’, Preprint, 2023, arXiv:2208.12404.Google Scholar
Culler, M. and Morgan, J. W., ‘Group actions on $\mathbb{R}$ -trees’, Proc. Lond. Math. Soc. (3) 55(3) (1987), 571–604.CrossRefGoogle Scholar
Gilman, J., ‘Two-generator discrete subgroups of ${}\mathrm{PSL}_2\left(\mathbb{R}\right)$ ’, Mem. Amer. Math. Soc. 117 (1995), 561.Google Scholar
Gromov, M., ‘Hyperbolic groups’, in: Essays in Group Theory, Mathematical Sciences Research Institute Publications, 8 (ed. Gersten, S. M.) (Springer, New York, 1987), 75–263.CrossRefGoogle Scholar
Jørgensen, T., ‘On discrete groups of Möbius transformations’, Amer. J. Math. 98(3) (1976), 739–749.CrossRefGoogle Scholar
Jørgensen, T., ‘A note on subgroups of $\mathrm{SL}_2\left(\mathbb{C}\right)$ ’, Quart. J. Math. Oxford Ser. (2) 28(110) (1977), 209–211.CrossRefGoogle Scholar
Jørgensen, T. and Kiikka, M., ‘Some extreme discrete groups’, Ann. Acad. Sci. Fenn. Ser. A I Math. 1(2) (1975), 245–248.CrossRefGoogle Scholar
Jørgensen, T. and Klein, P., ‘Algebraic convergence of finitely generated Kleinian groups’, Quart. J. Math. Oxford Ser. (2) 33(131) (1982), 325–332.CrossRefGoogle Scholar
Kato, F., ‘Non-archimedean orbifolds covered by Mumford curves’, J. Algebraic Geom. 14(1 (2005), 1–34.CrossRefGoogle Scholar
Kramer, L., ‘Some remarks on proper actions, proper metric spaces, and buildings’, Adv. Geom. 22(4) (2022), 541–559.CrossRefGoogle Scholar
Kuranishi, M., ‘On everywhere dense imbedding of free groups in Lie groups’, Nagoya Math. J. 2 (1951), 63–71.CrossRefGoogle Scholar
Lubotzky, A., ‘Lattices of minimal covolume in $\mathrm{SL}_2$ : a nonarchimedean analogue of Siegel’s Theorem $\mu \ge \pi /21$ ’, J. Amer. Math. Soc. 3(4) (1990), 961–975.Google Scholar
Martin, G. J., ‘On discrete Möbius groups in all dimensions: a generalization of Jørgensen’s inequality’, Acta Math. 163(3–4) (1989), 253–289.CrossRefGoogle Scholar
Morgan, J. W. and Shalen, P. B., ‘Valuations, trees, and degenerations of hyperbolic structures I’, Ann. of Math. (2) 120(3) (1984), 401–476.CrossRefGoogle Scholar
Qiu, W. Y., Yang, J. H. and Yin, Y. C., ‘The discrete subgroups and Jørgensen’s inequality for $(m,{\mathbb{C}}_p)$ ’, Acta Math. Sin. 29(3) (2013), 417–428.CrossRefGoogle Scholar
Scott, G. P., ‘Finitely generated 3-manifold groups are finitely presented’, J. Lond. Math. Soc. (2) 6 (1973), 437–440.CrossRefGoogle Scholar
Serre, J.-P., Local Fields (Springer-Verlag, New York, 1979); translated by M. J. Greenberg.CrossRefGoogle Scholar
Serre, J.-P., Trees (Springer-Verlag, Berlin, 1980); translated by J. Stillwell.CrossRefGoogle Scholar
Tits, J., ‘Free subgroups in linear groups’, J. Algebra 20 (1972), 250–270.CrossRefGoogle Scholar
Tits, J., ‘A theorem of Lie–Kolchin for trees’, in: Contributions to Algebra: A Collection of Papers Dedicated to Ellis-Kolchin (eds. Bass, H., Cassidy, P. J. and Kovacic, J.) (Academic Press, New York, 1977), 377–388.CrossRefGoogle Scholar
Wehrfritz, B., Infinite Linear Groups (Springer-Verlag, New York, 1973).CrossRefGoogle Scholar