Hostname: page-component-669899f699-g7b4s Total loading time: 0 Render date: 2025-04-29T23:55:49.237Z Has data issue: false hasContentIssue false
  • English
  • Français

ON HIGHER DIMENSIONAL ARITHMETIC PROGRESSIONS IN MEYER SETS

Part of: Sequences and sets Discrete geometry

Published online by Cambridge University Press:  06 December 2021

ANNA KLICK  and
NICOLAE STRUNGARU Open the ORCID record for NICOLAE STRUNGARU [Opens in a new window]
ANNA KLICK
Affiliation:
Department of Mathematical Sciences, MacEwan University, 10700 – 104 Avenue, Edmonton, AB T5J 4S2, Canada and Fakultät für Mathematik, Universität Bielefeld, Postfach 100131, 33501 Bielefeld Germany e-mail: [email protected]
NICOLAE STRUNGARU*
Affiliation:
Department of Mathematical Sciences, MacEwan University, 10700 – 104 Avenue, Edmonton, AB T5J 4S2, Canada and Institute of Mathematics ‘Simon Stoilow’, Bucharest, Romania
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper we study the existence of higher dimensional arithmetic progressions in Meyer sets. We show that the case when the ratios are linearly dependent over ${\mathbb Z}$ is trivial and focus on arithmetic progressions for which the ratios are linearly independent. Given a Meyer set 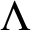$\Lambda $ and a fully Euclidean model set 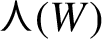with the property that finitely many translates of 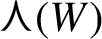cover 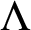$\Lambda $ , we prove that we can find higher dimensional arithmetic progressions of arbitrary length with k linearly independent ratios in 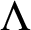$\Lambda $ if and only if k is at most the rank of the ${\mathbb Z}$ -module generated by 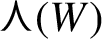. We use this result to characterize the Meyer sets that are subsets of fully Euclidean model sets.

Keywords

Meyer setsmodel setscut-and-project schemesarithmetic progressionsrank

MSC classification

Primary: 11B25: Arithmetic progressions
Secondary: 52C23: Quasicrystals, aperiodic tilings
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 114 , Issue 3 , June 2023 , pp. 312 - 336
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

Footnotes

Communicated by Michael Coons

The work was supported by NSERC with grant 2020-00038; we are grateful for the support.

References

Aedo, I., Grimm, U., Nagai, Y. and Staynova, P., ‘On long arithmetic progressions in binary Morse-like words’, Preprint, 2021, arXiv:2101.02056.CrossRefGoogle Scholar
Baake, M. and Grimm, U., ‘A comment on the relation between diffraction and entropy’, Entropy 14 (2012), 856–864.CrossRefGoogle Scholar
Baake, M. and Grimm, U., Aperiodic Order. Vol. 1: A Mathematical Invitation (Cambridge University Press, Cambridge, 2013).CrossRefGoogle Scholar
Baake, M., Lenz, D. and Richard, C., ‘Pure point diffraction implies zero entropy for Delone sets with uniform cluster frequencies’, Lett. Math. Phys. 82 (2007), 61–77.CrossRefGoogle Scholar
Baake, M. and Moody, R. V., ‘Weighted Dirac combs with pure point diffraction’, J. reine angew. Math. 573 (2004), 61–94.Google Scholar
Dummit, D. S. and Foote, R. M., Abstract Algebra, 3rd edn (Wiley, Hoboken, NJ, 2004).Google Scholar
Grillet, P. E., Abstract Algebra, Graduate Texts in Mathematics, 242 (Springer, New York, 2007).Google Scholar
Klick, A., Strungaru, N. and Tcaciuc, A., ‘On arithmetic progressions in model sets’, Discrete Comput. Geom., to appear. Published online (4 January 2021).CrossRefGoogle Scholar
Lagarias, J., ‘Meyer’s concept of quasicrystal and quasiregular sets’, Comm. Math. Phys. 179 (1996), 365–376.CrossRefGoogle Scholar
Lagarias, J., ‘Mathematical quasicrystals and the problem of diffraction’, in: Directions in Mathematical Quasicrystals, CRM Monograph Series, 13 (eds. Baake, M. and Moody, R. V.) (American Mathematical Society, Providence, RI, 2000), 61–93.Google Scholar
Lenz, D., Spindeler, T. and Strungaru, N., ‘Pure point diffraction and mean, Besicovitch and Weyl almost periodicity’, Preprint, 2020, arXiv:2006.10821.Google Scholar
Maddux, R. D., ‘Gallai’s theorem’, Preprint, 2014, arxiv:1411.1038.Google Scholar
Meyer, Y., Algebraic Numbers and Harmonic Analysis (North-Holland, Amsterdam, 1972).Google Scholar
Moody, R. V., ‘Meyer sets and their duals’, in: The Mathematics of Long-Range Aperiodic Order, NATO ASI Series, C489 (ed. Moody, R. V.) (Kluwer, Dordrecht, 1997), 403–441.CrossRefGoogle Scholar
Moody, R. V., ‘Model sets: a survey’, in: From Quasicrystals to More Complex Systems (eds. Axel, F., Dénoyer, F. and Gazeau, J. P.) (EDP Sciences, Les Ulis and Springer, Berlin, 2000), 145–166.CrossRefGoogle Scholar
Nagai, Y., Akiyama, S. and Lee, J. Y., ‘On arithmetic progressions in non-periodic self-affine tilings’, Ergodic Theory Dynam. Systems, to appear. Published online (15 June 2021).CrossRefGoogle Scholar
Richard, C., ‘Dense Dirac combs in Euclidean space with pure point diffraction’, J. Math. Phys. 44 (2003), 4436–4449.CrossRefGoogle Scholar
Schlottmann, M., ‘Generalized model sets and dynamical systems’, in: Directions in Mathematical Quasicrystals, CRM Monograph Series, 13 (eds. Baake, M. and Moody, R. V.) (American Mathematical Society, Providence, RI, 2000), 143–159.Google Scholar
Shechtman, D., Blech, I., Gratias, D. and Cahn, J. W., ‘Metallic phase with long-range orientational order and no translation symmetry’, Phys. Rev. Lett. 53 (1984), 183–185.CrossRefGoogle Scholar
Strungaru, N., ‘Almost periodic measures and long-range order in Meyer sets’, Discrete Comput. Geom. 33 (2005), 483–505.CrossRefGoogle Scholar
Strungaru, N., ‘On the Bragg diffraction spectra of a Meyer set’, Canad. J. Math. 65 (2013), 675–701.CrossRefGoogle Scholar
Strungaru, N., ‘On weighted Dirac combs supported inside model sets’, J. Phys. A 47 (2014), 335202.CrossRefGoogle Scholar
Strungaru, N., ‘Almost periodic pure point measures’, in: Aperiodic Order. Vol. 2: Crystallography and Almost Periodicity (eds. Baake, M. and Grimm, U.) (Cambridge University Press, Cambridge, 2017), 271–342.CrossRefGoogle Scholar
Strungaru, N., ‘On the Fourier analysis of measures with Meyer set support’, J. Funct. Anal. 278 (2020), 108404.CrossRefGoogle Scholar
Strungaru, N., ‘Why do Meyer sets diffract?’, Preprint, 2021, arXiv:2101.10513.Google Scholar
van der Waerden, B. L., ‘Beweis einer Baudetschen Vermutung’, Nieuw Arch. Wiskd. (5) 15 (1927), 212–216 (in German).Google Scholar